深度学习基础知识①
本学期学习了深度学习这门课,本着复习的想法,记录一下深度学习的相关知识
监督学习
机器学习分为监督学习,无监督学习和半监督学习。
监督学习,通过已有的训练样本去训练得到一个最优模型,再利用这个模型将所有的输入映射为相应的输出,对输出进行简单的判断从而实现预测和分类的目的,也就具有了对未知数据进行预测和分类的能力。简单来说,就像有标准答案的练习题,然后再去考试,相比没有答案的练习题然后去考试准确率更高。监督学习中的数据中是提前做好了分类信息的, 它的训练样本中是同时包含有特征和标签信息的,因此根据这些来得到相应的输出。
无监督学习
即训练样本的标记信息未知, 目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础,此类学习任务中研究最多、应用最广的是"聚类"(clustering),聚类目的在于把相似的东西聚在一起,主要通过计算样本间和群体间距离得到。
卷积神经网络相关知识
①常用激活函数
Relu函数h(x)=max{x,0}
sigmoid函数h(x)=1/(1+exp(-x))∈[0,1]
②CNN的层的连接顺序是“Convolution - ReLU -(Pooling)“是一个基本模块
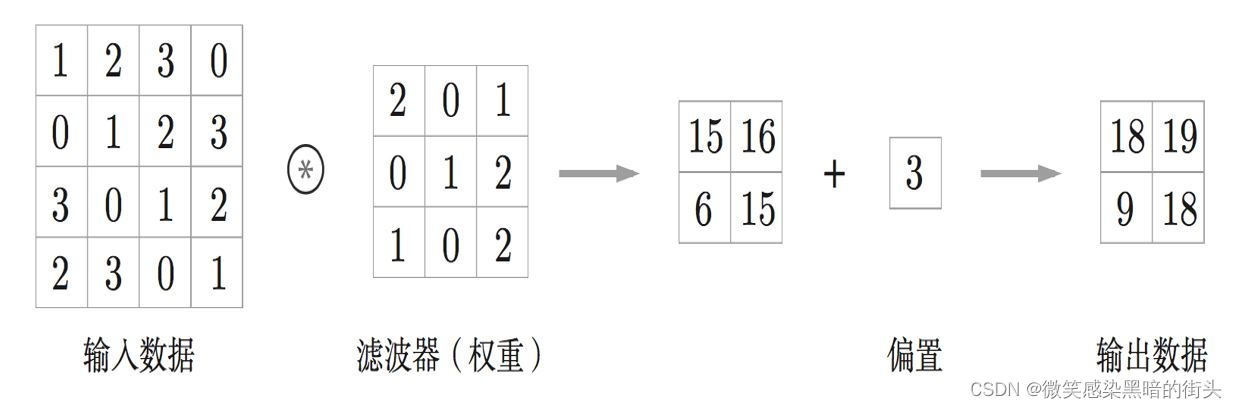
③卷积层相关知识
-
CNN 中,将卷积层的输入输出数据称为特征图(feature map)。其中,卷积层的输入数据称为输入特征图(input
featuremap),输出数据称为输出特征图(output feature map) 卷积运算:提取图像特征 -
在全连接的神经网络中,除了权重参数,还存在偏置。CNN 中,滤波 器的参数就对应之前的权重。并且,CNN 中也存在偏置。
-
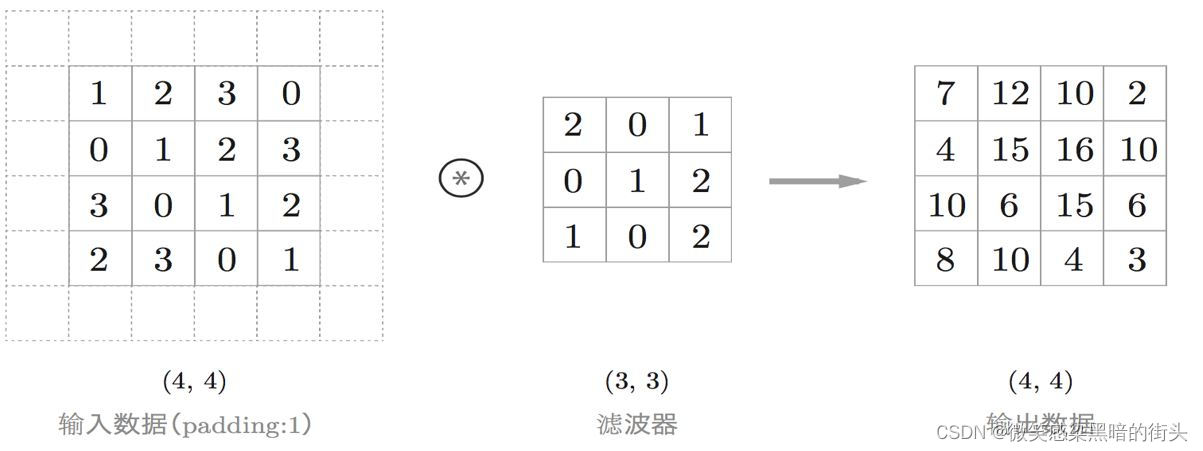
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比如 0
等),这称为填充(padding),是卷积运算中经常会用到的处理。使用填充主要是为了调整输出的大小。如下图, 通过填充,大小为 (4, 4) 的输入数据变成了 (6, 6) 的形状。 然后,应用大小为 (3, 3) 的滤波器,生成了大小为 (4, 4) 的输出数据。这个例 子中将填充设成了 1,不过填充的值也可以设置成 2、3 等任意的整数
-
应用滤波器的位置间隔称为步幅(stride)。之前的例子中步幅都是 1,如果将步幅设为 2,应用滤波器的窗口的间隔变为 2 个元
- 卷积运算输出的公式如下***:假设输入大小为 (H, W),滤波器大小为 (FH, FW),输出大小为 (OH, OW),填充为P,步幅为 S。此时,输出大小可通过下式 进行计算。

输入大小:(4, 4);填充:1;步幅:1;滤波器大小:(3, 3) 输出的大小为 :

3 维数据的卷积运算
这里以 3 通道的数据为例,可以发现纵深方向(通道方向)上特征图增加了。通道方向上有多个特征图时,会按通道 进行输入数据和滤波器的卷积运算,并将结果相加,从而得到输出
需要注意的是,在 3 维数据的卷积运算中,输入数据和滤波器的通道数 要设为相同的值。在这个例子中,输入数据和滤波器的通道数一致,均为 3。 滤波器大小可以设定为任意值(不过,每个通道的滤波器大小要全部相同)。
把 3 维数据表示为多维数组 时,书写顺序为(channel, height, width)。比如,通道数为C、高度为H、 长度为 W 的数据的形状可以写成(C, H, W)。滤波器也一样,通道数为 C、滤波器高度为 FH(FilterHeight)、长度为 FW(Filter Width)时,可以写成(C, FH, FW)。 可以这样理解一个滤波器和一组RGB图像进行卷积运算会生成一维的特征图
可以这样理解一个滤波器和一组RGB图像进行卷积运算会生成一维的特征图
通过应用 FN 个滤波器,输出特征图也生成了 FN 个。如果 将这 FN 个特征图汇集在一起,就得到了形状为 (FN, OH, OW) 的方块。将 这个方块传给下一层,就是 CNN 的处理流。
关于卷积运算的滤波器,也必须考虑滤波器的数量。
因此,作为 4 维数据,滤波器的权重数据要按 (output_channel, input_ channel, height, width) 的顺序书写。比如,通道数为 3、大小为 5 × 5 的滤 波器有 20 个时,可以写成 (20, 3, 5, 5)
这个output_channel其实是滤波器的个数

每个通道只有一个偏置。这里,偏置的形状是 (FN, 1, 1)

批处理
神经网络的处理中进行了将输入数据打包的批处理。之前的全连接神经 网络的实现也对应了批处理。
我们希望卷积运算也同样对应批处理。为此,需要将在各层间传递的数 据 保 存 为 4 维 数 据。具 体 地 讲,就 是 按 (batch_num, channel, height, width) 的顺序保存数据。比如,将上图 中的处理改成对 N 个数据进行批处理时, 数据的形状如下图 所示

⑦池化操作
池化分为max pooling 和 average pooling即最大池化和平均池化。“Max 池化”是获取最大值的运算,Average 池化则是计算目标区域的平均值
下图的例子是按步幅 2 进行 2 × 2 的 Max 池化时的处理顺序。“Max 池化”是获取最大值的运算,“2 × 2”表示目标区域的大小。
如图所示,从 2 × 2 的区域中取出最大的元素。此外,这个例子中将步幅设为了 2,所以 2 × 2 的窗口的移动间隔为 2 个元素。另外,一般来说,池化的窗口大小会 和步幅设定成相同的值。比如,3 × 3 的窗口的步幅会设为 3,4 × 4 的窗口 的步幅会设为 4 等。
池化层的特征
没有要学习的参数
池化层和卷积层不同,没有要学习的参数。池化只是从目标区域中取最 大值(或者平均值),所以不存在要学习的参数。
通道数不发生变化
经过池化运算,输入数据和输出数据的通道数不会发生变化,计算是按通道独立进行的。