一、霍夫变换Hough
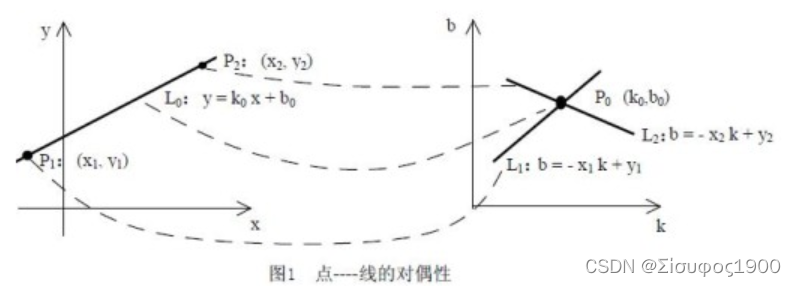
? ? ? ?Hough变换是图像处理中从图像中识别几何形状的基本方法之一。Hough变换的基本原理在于利用点与线的对偶性,将原始图像空间的给定的曲线通过曲线表达形式变为参数空间的一个点。这样就把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。
二、霍夫空间
在一个xOy 的坐标系空间里,经过(x1,y1)的直线有无数条,我们可以用a(斜率)和b(截距)来表示? ? ? ? yi=axi+b,如果我们将这个(x1,y1)当成一个常量,那么我们可以用(x1,y1)来表示a和b,因此我们吧aOb构成的空间称之为霍夫空间。
? ? b=-x1a+y1,图像表示如下,右边的就是霍夫空间,我们也称之为参数空间
假如有直线是y=x, 取上面的三个点:A(0,0), B(1,1), C(22)。
那么过A点的直线的参数是:0=0+b--L1,
过B点的直线的参数要满足方程:1=k+b --L2,
过C点的直线的参数要满足方程:2=2k+b--L3,
L1、L2、L3 对应着参数平面上的三条直线,而这三条直线会相交于一点(k=1,b=0)。把图像平面上的点对应到参数平面上的线,若xOy上有两条直线,那么在霍夫空间就会看到两个峰值点。
??霍夫变换的思想
? ? 在xOy坐标系下的一个点在参数坐标系中的一条直线,反之一样,在xOy坐标系下一条直线的所有点,它们的斜率和截距是相同的,所以它们在参数坐标系下对应于同一个点。
三、霍夫直线

如上图所示,可以转换到极坐标空间(数学推导就不写了)。
如何验证xoy 平面内的(x1,y 1),(x2, y 2),…是否共线?
只要曲线ρ=xi ?cosθ+y i ?sinθ,i=1,2,…在θoρ平面内相交于一个点 就可以了,如下图

?如何在xoy平面找出哪些点在同一条直线上?
? ? 若xoy 平面内有5个点,对应到θoρ平面(霍夫空间)的5条 曲线,可以看出1、2、3、4点对应的曲线是相交于一个点的,所以xoy 平面内的1、2、 3、4点是共线的;同样,5点和4点对应的曲线也相交于一个点,所以xoy 平面内的5点和4 点是共线的,如下图: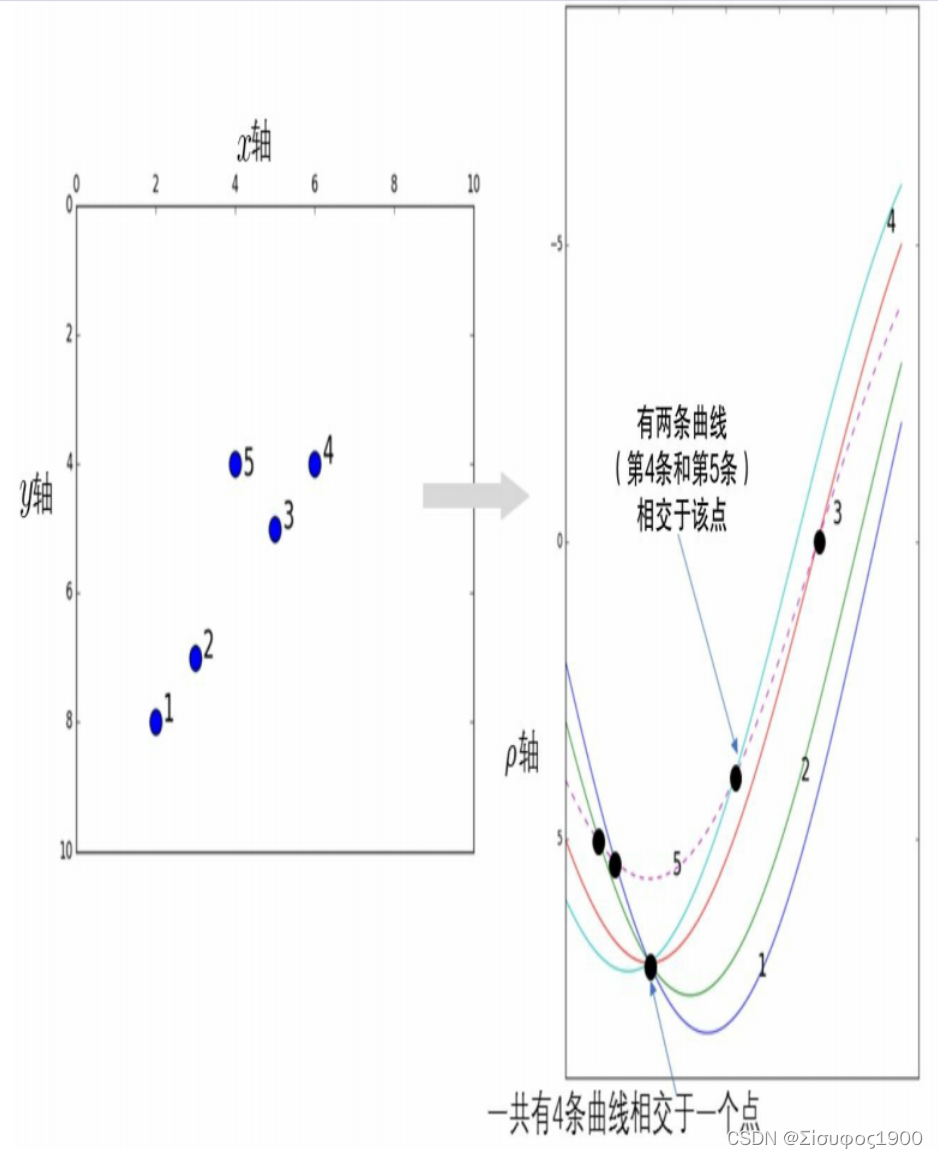
?结 论 :
? ? ? ?要判断xoy 平面内哪些点是共线的,首先求出每一个点对应到霍夫空间的曲线,然后判断哪几条曲线相交于一点,最后将相交于一点的曲线反过来对应到xoy 平面内 的点,这些点就是共线的,这就是在图像中进行标准霍夫直线检测的核心思想
c++实现解析
首先,霍夫直线处理的是一个二值图像,并且一般都是黑色背景
投票器
那么如何利用计算出的θoρ空间中的这些点去验证哪些像素点是共线的呢?是用曲线相交方式来验证的,但是这里只是从曲线上取了一些离散的点,所以需要 引入一个工具,称为“计数器”,或者“投票器”,或者二维直方图。
?如上面的例子的投票结果如下: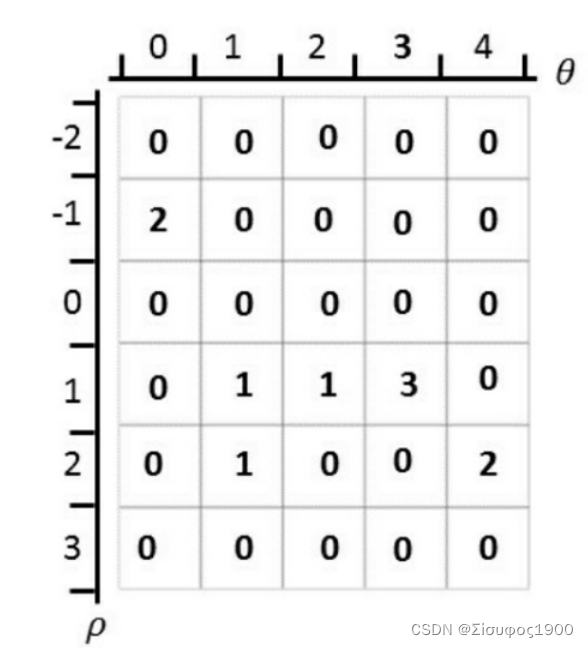
?构造霍夫空间中的计数器
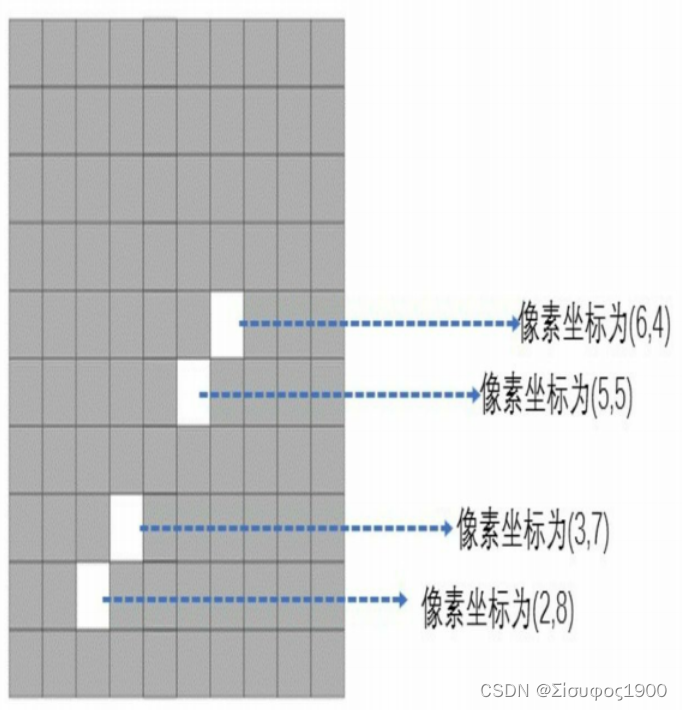
若在xoy 平面内有任意一点(x1,y 1),过该点有无数条直线,但是原点到这些直线的距离不会超过sqrt(pow(x1,2)+pow(y1,2))=r。图像矩阵宽度为W、高度为H,那么可以构造以下计数器,用L代表整数r+1:
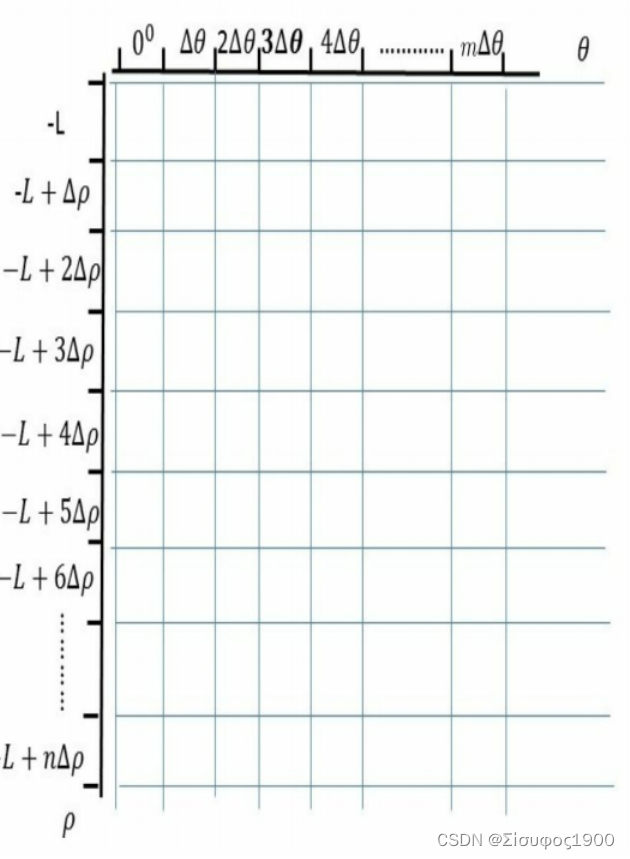
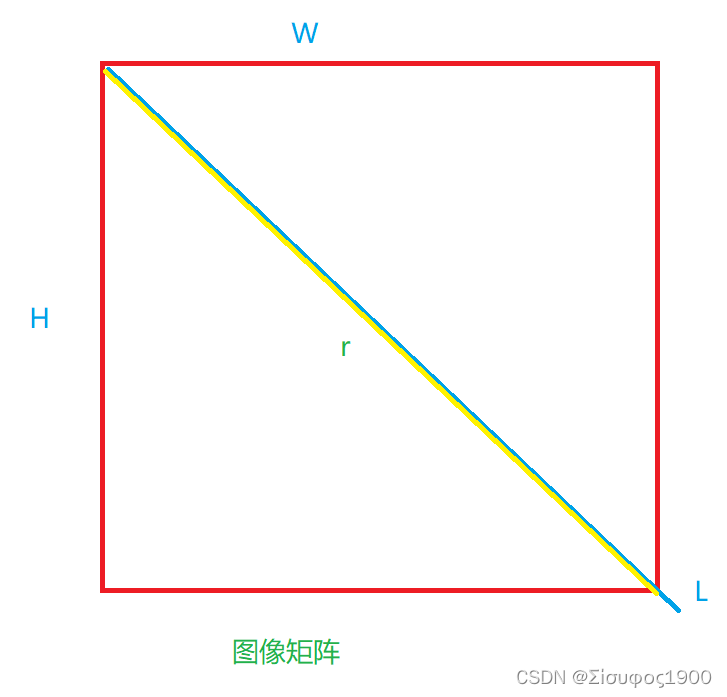
?若图像宽度为10、高度为10,所以L=r+1=15,四个前景像素点的坐标分别为(6,4)、(5,5)、(3,7)、(2,8),那么所有霍夫 空间中的点坐标一共有4×180个(步长=1),(45°,round(6 cos 45°+4 sin 45°))=(45°, 7),(45°,round(5 cos 45°+5 sin 45°))=(45°,7),(45°,round(3 cos 45°+7 sin 45°))=(45°,7),(45°,round(2 cos 45°+8 sin 45°))=(45°,7)等,投票计数器中,在计数器(45°,7)这个位置的计数是4,这里的(45°,7)出现了4次,表明有四个像素点是共线的。
?实现步骤
1)读取一幅带处理二值图像,最好背景为黑色;
2)获取图像空间的源像素数据;
3)通过量化霍夫参数空间为有限个值间隔等分或者累加格子,即r,θ;
4)霍夫变换算法开始,每个像素坐标点P(x, y)被转换到(r, θ)的曲线点上面,并累加到对应的格子数据点;
5)寻找最大霍夫值,设置阈值,反变换到图像空间
霍夫直线算子
//void HoughLinesP(
// InputArray image, //输入图像,即源图像,需为8位的单通道二进制图像
// OutputArray lines,//OutputArray类型的lines ,经过调用HoughLinesP函数后后存储了检测到的线条的输出矢量,每一条线由具有四个元素的矢量(x_1,y_1, x_2, y_2) 表示,其中,(x_1, y_1)和(x_2, y_2) 是是每个检测到的线段的结束点
// double rho, // 角度步长
// double theta, // 以弧度为单位的角度精度的
// int threshold, //累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。大于阈值threshold的线段才可以被检测通过并返回到结果中
// double minLineLength = 0,//有默认值0,表示最低线段的长度,比这个设定参数短的线段就不能被显现出来。
// double maxLineGap = 0)//有默认值0,允许将同一行点与点之间连接起效果如下
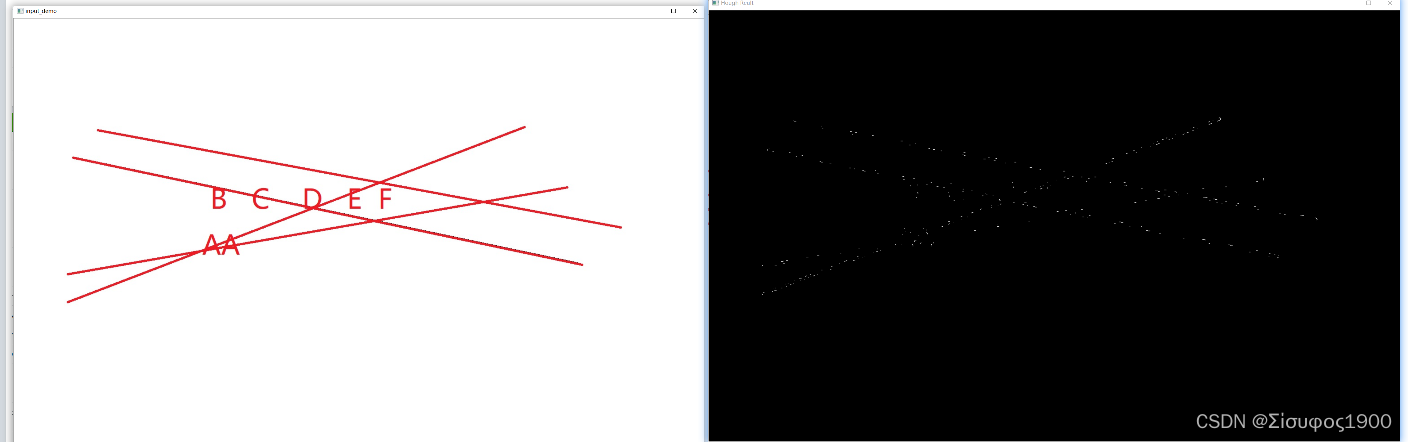
?HoughLinesP算子实现
待续。。。。。