《OTFS 技术研究现状与展望 》
背景:
正交频分复用(orthogonal frequency division multiplexing,OFDM)技术由于其高频谱效率及抗多径干扰能力,在 4G 和 5G 系统中广泛应用,但是其在时频双选(高时延、高多普勒频移)信道下性能不佳。高速移动和高频段带来的高多普勒频移会严重破坏 OFDM 子载波之间的正交性。虽然 5G 系统中的OFDM 采用了更大、更灵活的子载波间隔设计,但是子载波间隔的增大会导致循环前缀(cyclic prefix,CP)变短,抗多径能力下降,不能同时满足时频双选信道下的需求。
原理:
正交时频空(orthogonal time and frequency space,OTFS)技术,以在时频双选信道下实现高可靠和高速率的数据传 输 。 OTFS 技 术 直 接 在 时 延 — 多 普 勒(delay-Doppler, DD)域进行数据调制并且在整个时频域上扩展。当使用合适的接收机时,OTFS能够获得时间和频率上的全部信道分集。OTFS技术将时变多径信道变换到 DD 域上,使得传输单元中的所有符号都经历几乎相同且变化缓慢的
稀疏信道。此外,由于所有调制符号在时频域上均匀扩展,OTFS 信号的峰均比(peak-to averagepower ratio,PAPR)比 OFDM 更低。

如图 1 所示,OTFS 技术中数据调制符号产生于 DD 域:
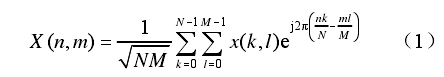
从式(1)中可以看出,每一个调制符号都由一个二维正交基函数扩展到时频域上,即 OTFS 可看
作一种时频二维扩展技术式(1)中还可以看出,ISFFT 可以通过对 DD 域信号矩阵的列和行分别
进行 M 点离散傅里叶变换(discrete Fourier transform,DFT)和 N 点逆离散傅里叶变换(inverse
DFT,IDFT)实现。
在接收端使用发送端的逆操作,首先通过魏格纳(Wigner)变换将接收信号从时域转换到时
频域,再通过 SFFT 变换从时频域变换到 DD 域:
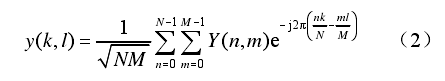
OTFS 可以与已有的多载波调制技术兼容,将图 1 中的海森堡变换特化为 IFFT,魏格纳变换
特化为 FFT,内侧虚线框中就是一个 OFDM 系统。因此,在 OFDM 系统的发送端增加 ISFFT 预处理
模 块 , 在 接 收 端 增 加 SFFT 模 块 即 可 实 现OTFS。
海森堡变换:
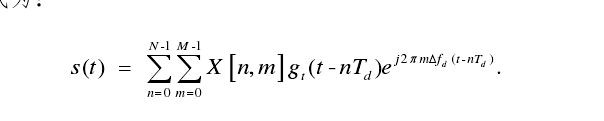
当公式中的成型滤波函数是个理想的矩型窗函数时,Heisenberg 变换则退化为传统的 IDFT 变换。
研究方向:
基于 OTFS 的多址接入
由于 DD 域上发送信号和信道是二维循环卷积的关系,在多径信道下,发送端 DD 域上正交的信号在接收端并不正交,因此 OTFS 下的多址接入方式是一个值得深入研究的方向。
OTFS 多址接入技术可以分为正交多址接入和非正交多址接入,也可以分为 DD 域多址接入和时频域多址接入。在 DD 域上分配资源共有 3 种方式,即沿时延轴分配、沿多普勒轴分配和块状分配。在 DD 域分配连续的资源会导致多用户干扰,虽然可以采用保护间隔来避免,但会影响到频谱效率。
OTFS 导频设计和信道估计
在 OTFS 系统中,如果时延和多普勒分辨力足够,信道在 DD 域上呈现若干个稀疏的冲激的形式。因此,目前常见的 DD 域导频周围有多个保护间隔符号的冲激信号,如图 3 所示。在无分数多普勒时,DD 域上的信道不会产生弥散,信道冲激响应的范围会局限在最大多普勒偏移和最大时延内。此方案可进一步推广到多输入多输出(multi-input and multi-output,MIMO)和多用户的导频设计,可以利用信道在 DD 域上的稀疏性以增强信道估计和跟踪的精度。基于图3 中的导频设计,文献[27]中提出了简单的基于阈值的信道估计。

OTFS 中的信道估计在现实应用中面临的一个重要问题是分数多普勒弥散。若帧长足够长,
多普勒频移的分辨率足够高,则不存在分数多普勒弥散问题。此时每个调制符号具有相同且慢变
的信道增益。然而,在实际应用中,帧长有限,分数多普勒频移不可忽略,多普勒分辨率的不足导致信道在多普勒域上弥散。文献[28]提出,当分数多普勒频移存在时,需要对导频设计方案进行调整,使得保护间隔包括最大时延范围内的全部多普勒域。此外,采用非双正交波形时,载波间干扰在 DD 域上表现为时延域符号信道的相位差,该相位差的大小与多普勒频移有关。根据导频信号进行信道估计后,还需要对该相位差进行补偿。
OTFS 接收机研究:
OTFS 系统中在 DD 域产生信号,接收信号由发送信号和 DD 域信道二维卷积而得,这区别于传统 OFDM 子载波内平坦的信道。因此,接收机算法是 OTFS 技术中极其重要的研究内容。**OTFS接收机可以分为线性接收机和非线性接收机。**非线性接收机具有接近最大似然的性能但复杂度较高且灵活性较差,而线性接收机虽然复杂度低但性能有损失。
非线性接收机
目前常见的非线性接收机是消息传递(message passing,MP)接收机。在无分数多普勒频移时,DD 域信道表现出稀疏性。即使存在分数多普勒 弥 散 , 通 过 适 当 方 式 补 偿 多 普 勒 间 干 扰(inter-Doppler interference)后,信道矩阵仍具备稀疏性。此时,每个输入(发送)符号仅作用于少数输出(接收)符号,而每个输出符号也仅与少数输入符号相关。如图 5 所示,基于迭代的置信传播结构中,输入符号向输出符号传递概率消息,而输出符号向输入符号传递干扰和噪声的均值和方差,干扰项近似为高斯噪声以降低复杂度。MP 接收机的改进,主要有降低复杂度和优化性能两个方向。目前也有其他非线性接收机的研究,如基于最大比合并的 Rake 迭代接收机和变分贝叶斯接收机等。

线性接收机
TFS 中的线性接收机可分为 DD 域线性接收机和时频域线性接收机两类。DD 域接收机的性能 相 比 于 时 频 域 更 好 , 但 复 杂 度 更 高 。基于 DD 域信道矩阵的特殊结构,文献[31]中研究了低复杂度线性接收机。时频域接收机的复杂度很低,为O(MN) ,但缺点是性能有所损失。时频域接收机的增强,可以通过 DD 域的均衡器来消除多普勒扩展所带来的影响,或者是在时频域通过软符号反馈输出进行并行干扰消等,但代价是复杂度的增加。