[人工智能]吴恩达深度学习 5.1 序列模型-循环神经网络

1. 知识点：

• 序列模型的应用：

? ? ? ? 语音识别：输入的语音和输出的文本，都是序列数据 。

? ? ? ? 音乐生成：生成的音乐乐谱是序列数据。

? ? ? ? 情感分类：将输入的评论转换为相应的评价等级。输入是序列。

? ? ? ? 机器翻译：两种不同语言之间的转换。输入和输出都是序列。

? ? ? ? 视频行为识别：识别输入的视频帧序列中的人物行为。

? ? ? ? 命名实体识别：从输入的句子中识别实体的名字。

• 符号定义：

? ? ? ? 输入x：输入序列，如，“A snow year,a rich year”。表示输入序列x中的第t个符号。

? ? ? ? 输出y：输出序列，如，“10001010”。?表示输出序列y中的第t个符号。

? ? ? ? Tx表示输入x的长度。

? ? ? ? Ty表示输出y的长度。

? ? ? ??表示第i个输入样本的第t个符号。

? ? ? ? 用每个单词的编码（如one-hot编码）表示第一个输入符号：可以 实现输入x到输出y的转换。

• 传统神经网络：将输入序列X进行编码（比如one-hot编码），输入到多层神经网络中，得出输出Y

? ? ? ? 存在的问题：

? ? ? ? 1)对于不同的例子输入序列编码的长度不同

? ? ? ? 2)不能共享从文本不同位置学习到的特征（没咋看明白？？？）

• 循环神经网络：

? ? ? ? 每个单元有两个输出：1个输入序列元素，和1个激活值。

? ? ? ? 每个单元共享参数：，，。

? ? ? ? 激活值实现输出序列元素使用了从开始到当前的所有输入序列元素。

• 循环神经网络的前向传播：?

?

• 循环神经网络的后向传播和损失函数：

? ? ? ? 损失函数：,

? ? ? ? 反向传播：按照前向传播相反的方向进行导数计算

• 不同类型的RNN：

? ? ? ? 输入和输出长度相等：

? ? ? ? 多个输入元素和一个输出元素：比如，情感分类

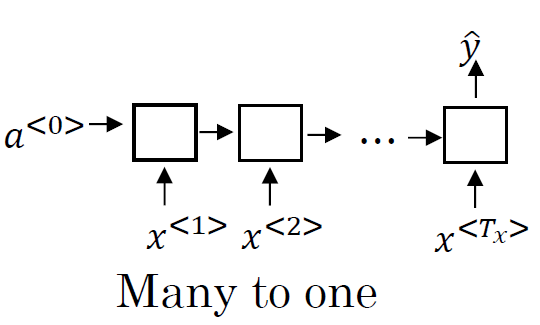
? ? ? ? 一个输入元素和多个输出元素：比如，音乐生成，输入一个音乐类型，生成音乐序列

? ? ? ? 多个输入元素和多个输出元素，输入和输出长度不等：比如，机器翻译

• 语言模型：评估句子中各个单词出现的可能性，进而评估整个句子出现的可能性。

• RNN语言模型：?

? ? ? ? 向量化：将句子中的单词使用字典进行向量化

? ? ? ? 输入：零向量+样本输入序列

? ? ? ? 标签：样本输入序列+结束元素

? ? ? ? 第一步：用零向量，对输出进行预测，即预测第一个单词

? ? ? ? 后面步骤：用前面的隐藏输入a和当前输入x，预测后面一个单词是某个单词的概率

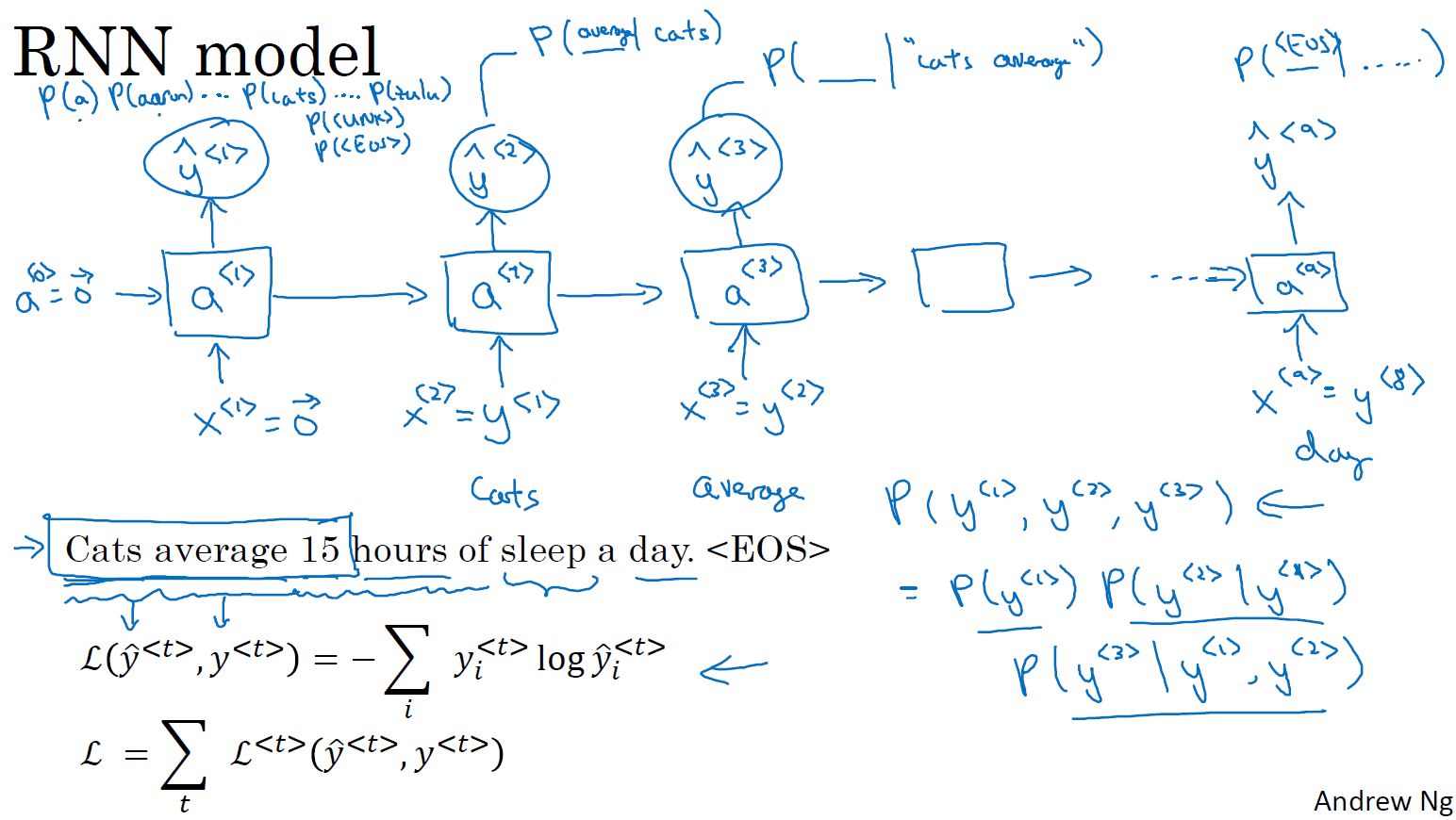
• 新序列采样：简单测试一个模型的学习效果

? ? ? ? 第一步：，计算第一个输出单词。

? ? ? ? 后面步骤：将作为下一个时间步的输入，预测下一个输出。

?

????????也有基于字符的语言模型：?

?

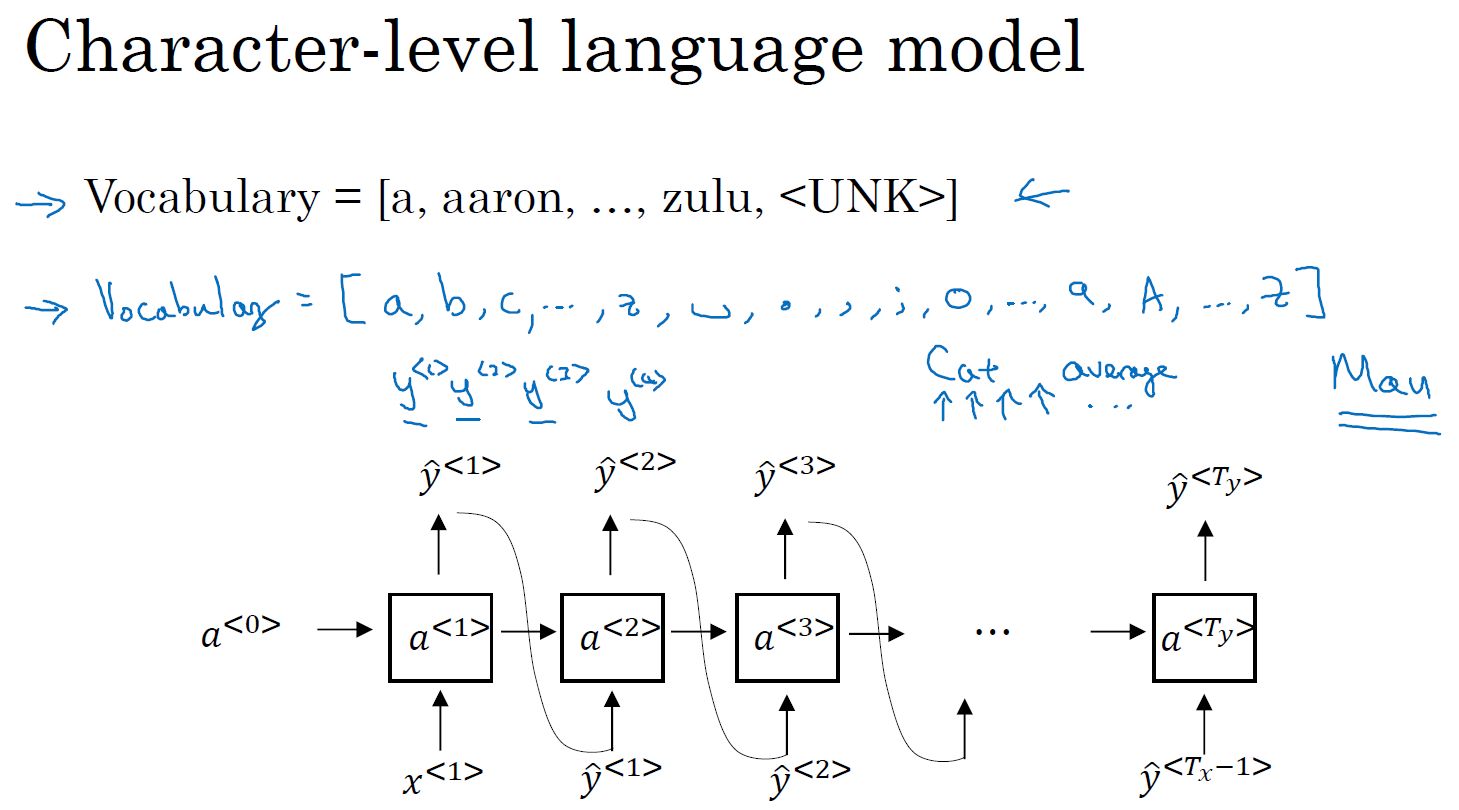
• RNN模型中不擅长捕获长期依赖总是：很难捕获前面的单词对后面远距离单词产生的影响

?

• RNN的GRU单元：

? ? ? ? 记忆单元候选当前值由记忆单元前一个值和输入当前值计算得出。

? ? ? ? 更新门由记忆单元前一个值和输入当前值计算得出，经sigmoid()运算，值在0~1之间。

? ? ? ? 记忆单元当前值由更新门、记忆单元候选值、记忆单元前一个值运算得出。这样可以通过更新门的作用给输入较大的权重。

?

• LSTM：? 在RNN的基础上增加了遗忘门和输出门，用更新门和遗忘门计算记忆单元，用输出门计算输出

?

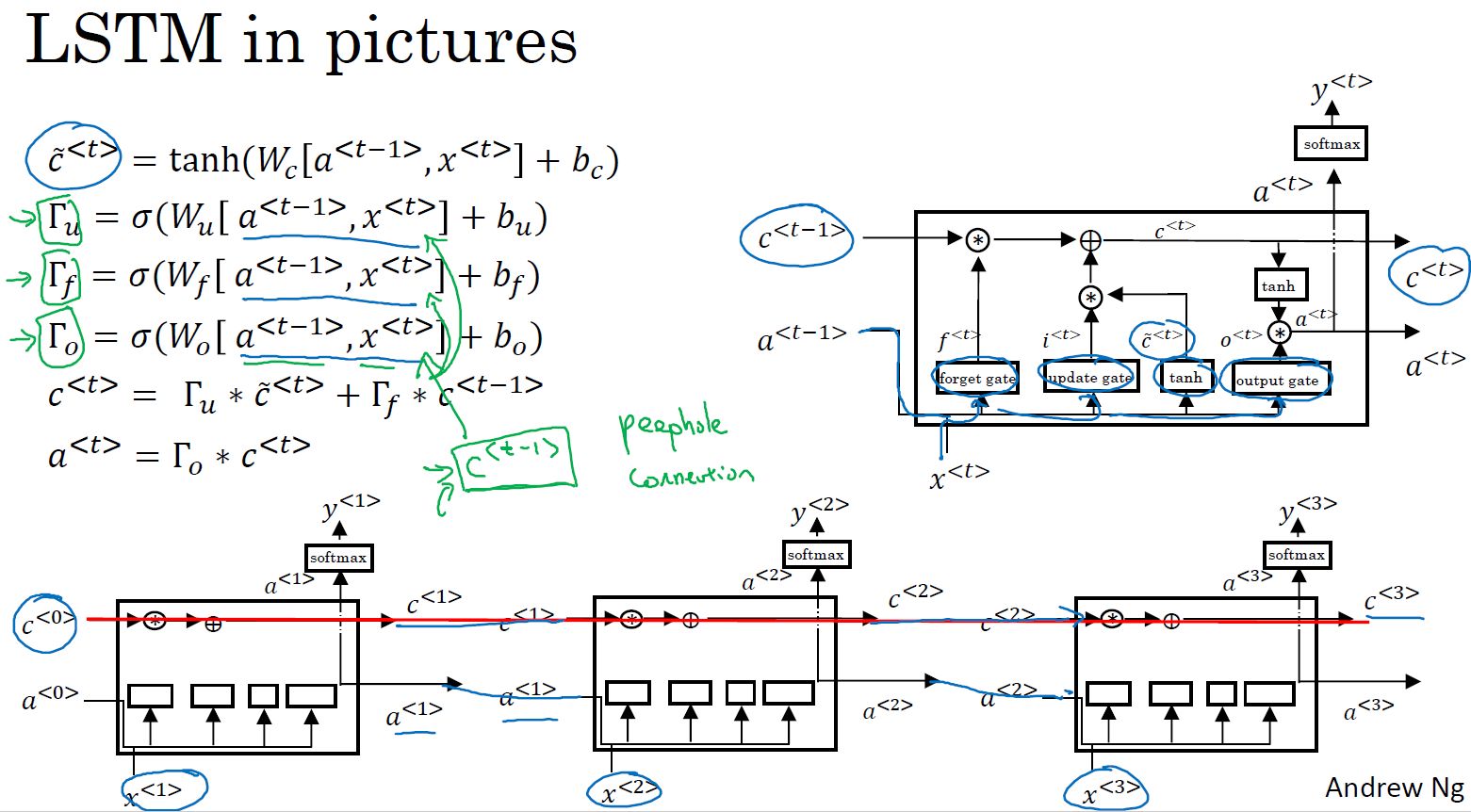
• 双向RNN：

? ? ? ? 单向RNN不能利用未来信息对当前信息进行预测

?

? ? ? ? 双向RNN：有前向连接层和反向连接层

? ? ? ? ? ? ? ? ? ? ? ?

• 深层RNN：对于RNN来说，三层神经网络已经很多了?

?

2. 应用实例：

import numpy as np
import rnn_utils

def rnn_cell_forward(xt, a_prev, parameters):
    """
    根据图2实现RNN单元的单步前向传播
    
    参数：
        xt -- 时间步“t”输入的数据，维度为（n_x, m）
        a_prev -- 时间步“t - 1”的隐藏隐藏状态，维度为（n_a, m）
        parameters -- 字典，包含了以下内容:
                        Wax -- 矩阵，输入乘以权重，维度为（n_a, n_x）
                        Waa -- 矩阵，隐藏状态乘以权重，维度为（n_a, n_a）
                        Wya -- 矩阵，隐藏状态与输出相关的权重矩阵，维度为（n_y, n_a）
                        ba  -- 偏置，维度为（n_a, 1）
                        by  -- 偏置，隐藏状态与输出相关的偏置，维度为（n_y, 1）
    
    返回：
        a_next -- 下一个隐藏状态，维度为（n_a， m）
        yt_pred -- 在时间步“t”的预测，维度为（n_y， m）
        cache -- 反向传播需要的元组，包含了(a_next, a_prev, xt, parameters)
    """
    
    # 从“parameters”获取参数
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]
    
    # 使用上面的公式计算下一个激活值
    a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
    
    # 使用上面的公式计算当前单元的输出
    yt_pred = rnn_utils.softmax(np.dot(Wya, a_next) + by)
    
    # 保存反向传播需要的值
    cache = (a_next, a_prev, xt, parameters)
    
    return a_next, yt_pred, cache
    

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}

a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape)

a_next[4] =  [ 0.59584544  0.18141802  0.61311866  0.99808218  0.85016201  0.99980978
 -0.18887155  0.99815551  0.6531151   0.82872037]
a_next.shape =  (5, 10)
yt_pred[1] = [0.9888161  0.01682021 0.21140899 0.36817467 0.98988387 0.88945212
 0.36920224 0.9966312  0.9982559  0.17746526]
yt_pred.shape =  (2, 10)

def rnn_forward(x, a0, parameters):
    """
    根据图3来实现循环神经网络的前向传播
    
    参数：
        x -- 输入的全部数据，维度为(n_x, m, T_x)
        a0 -- 初始化隐藏状态，维度为 (n_a, m)
        parameters -- 字典，包含了以下内容:
                        Wax -- 矩阵，输入乘以权重，维度为（n_a, n_x）
                        Waa -- 矩阵，隐藏状态乘以权重，维度为（n_a, n_a）
                        Wya -- 矩阵，隐藏状态与输出相关的权重矩阵，维度为（n_y, n_a）
                        ba  -- 偏置，维度为（n_a, 1）
                        by  -- 偏置，隐藏状态与输出相关的偏置，维度为（n_y, 1）
    
    返回：
        a -- 所有时间步的隐藏状态，维度为(n_a, m, T_x)
        y_pred -- 所有时间步的预测，维度为(n_y, m, T_x)
        caches -- 为反向传播的保存的元组，维度为（【列表类型】cache, x)）
    """
    
    # 初始化“caches”，它将以列表类型包含所有的cache
    caches = []
    
    # 获取 x 与 Wya 的维度信息
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wya"].shape
    
    # 使用0来初始化“a” 与“y”
    a = np.zeros([n_a, m, T_x])
    y_pred = np.zeros([n_y, m, T_x])
    
    # 初始化“next”
    a_next = a0
    
    # 遍历所有时间步
    for t in range(T_x):
        ## 1.使用rnn_cell_forward函数来更新“next”隐藏状态与cache。
        a_next, yt_pred, cache = rnn_cell_forward(x[:, :, t], a_next, parameters)
        
        ## 2.使用 a 来保存“next”隐藏状态（第 t ）个位置。
        a[:, :, t] = a_next
        
        ## 3.使用 y 来保存预测值。
        y_pred[:, :, t] = yt_pred
        
        ## 4.把cache保存到“caches”列表中。
        caches.append(cache)
    
    # 保存反向传播所需要的参数
    caches = (caches, x)
    
    return a, y_pred, caches

np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}

a, y_pred, caches = rnn_forward(x, a0, parameters)
print("a[4][1] = ", a[4][1])
print("a.shape = ", a.shape)
print("y_pred[1][3] =", y_pred[1][3])
print("y_pred.shape = ", y_pred.shape)
print("caches[1][1][3] =", caches[1][1][3])
print("len(caches) = ", len(caches))

a[4][1] =  [-0.99999375  0.77911235 -0.99861469 -0.99833267]
a.shape =  (5, 10, 4)
y_pred[1][3] = [0.79560373 0.86224861 0.11118257 0.81515947]
y_pred.shape =  (2, 10, 4)
caches[1][1][3] = [-1.1425182  -0.34934272 -0.20889423  0.58662319]
len(caches) =  2

def lstm_cell_forward(xt, a_prev, c_prev, parameters):
    """
    根据图4实现一个LSTM单元的前向传播。
    
    参数：
        xt -- 在时间步“t”输入的数据，维度为(n_x, m)
        a_prev -- 上一个时间步“t-1”的隐藏状态，维度为(n_a, m)
        c_prev -- 上一个时间步“t-1”的记忆状态，维度为(n_a, m)
        parameters -- 字典类型的变量，包含了：
                        Wf -- 遗忘门的权值，维度为(n_a, n_a + n_x)
                        bf -- 遗忘门的偏置，维度为(n_a, 1)
                        Wi -- 更新门的权值，维度为(n_a, n_a + n_x)
                        bi -- 更新门的偏置，维度为(n_a, 1)
                        Wc -- 第一个“tanh”的权值，维度为(n_a, n_a + n_x)
                        bc -- 第一个“tanh”的偏置，维度为(n_a, n_a + n_x)
                        Wo -- 输出门的权值，维度为(n_a, n_a + n_x)
                        bo -- 输出门的偏置，维度为(n_a, 1)
                        Wy -- 隐藏状态与输出相关的权值，维度为(n_y, n_a)
                        by -- 隐藏状态与输出相关的偏置，维度为(n_y, 1)
    返回：
        a_next -- 下一个隐藏状态，维度为(n_a, m)
        c_next -- 下一个记忆状态，维度为(n_a, m)
        yt_pred -- 在时间步“t”的预测，维度为(n_y, m)
        cache -- 包含了反向传播所需要的参数，包含了(a_next, c_next, a_prev, c_prev, xt, parameters)
        
    注意：
        ft/it/ot表示遗忘/更新/输出门，cct表示候选值(c tilda)，c表示记忆值。
    """
    
    # 从“parameters”中获取相关值
    Wf = parameters["Wf"]
    bf = parameters["bf"]
    Wi = parameters["Wi"]
    bi = parameters["bi"]
    Wc = parameters["Wc"]
    bc = parameters["bc"]
    Wo = parameters["Wo"]
    bo = parameters["bo"]
    Wy = parameters["Wy"]
    by = parameters["by"]
    
    # 获取 xt 与 Wy 的维度信息
    n_x, m = xt.shape
    n_y, n_a = Wy.shape
    
    # 1.连接 a_prev 与 xt
    contact = np.zeros([n_a + n_x, m])
    contact[: n_a, :] = a_prev
    contact[n_a :, :] = xt
    
    # 2.根据公式计算ft、it、cct、c_next、ot、a_next
    
    ## 遗忘门，公式1
    ft = rnn_utils.sigmoid(np.dot(Wf, contact) + bf)
    
    ## 更新门，公式2
    it = rnn_utils.sigmoid(np.dot(Wi, contact) + bi)
    
    ## 更新单元，公式3
    cct = np.tanh(np.dot(Wc, contact) + bc)
    
    ## 更新单元，公式4
    #c_next = np.multiply(ft, c_prev) + np.multiply(it, cct)
    c_next = ft * c_prev + it * cct
    ## 输出门，公式5
    ot = rnn_utils.sigmoid(np.dot(Wo, contact) + bo)
    
    ## 输出门，公式6
    #a_next = np.multiply(ot, np.tan(c_next))
    a_next = ot * np.tanh(c_next)
    # 3.计算LSTM单元的预测值
    yt_pred = rnn_utils.softmax(np.dot(Wy, a_next) + by)
    
    # 保存包含了反向传播所需要的参数
    cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
    
    return a_next, c_next, yt_pred, cache

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
print("cache[1][3] =", cache[1][3])
print("len(cache) = ", len(cache))

a_next[4] =  [-0.66408471  0.0036921   0.02088357  0.22834167 -0.85575339  0.00138482
  0.76566531  0.34631421 -0.00215674  0.43827275]
a_next.shape =  (5, 10)
c_next[2] =  [ 0.63267805  1.00570849  0.35504474  0.20690913 -1.64566718  0.11832942
  0.76449811 -0.0981561  -0.74348425 -0.26810932]
c_next.shape =  (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
 0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape =  (2, 10)
cache[1][3] = [-0.16263996  1.03729328  0.72938082 -0.54101719  0.02752074 -0.30821874
  0.07651101 -1.03752894  1.41219977 -0.37647422]
len(cache) =  10

def lstm_forward(x, a0, parameters):
    """
    根据图5来实现LSTM单元组成的的循环神经网络
    
    参数：
        x -- 所有时间步的输入数据，维度为(n_x, m, T_x)
        a0 -- 初始化隐藏状态，维度为(n_a, m)
        parameters -- python字典，包含了以下参数：
                        Wf -- 遗忘门的权值，维度为(n_a, n_a + n_x)
                        bf -- 遗忘门的偏置，维度为(n_a, 1)
                        Wi -- 更新门的权值，维度为(n_a, n_a + n_x)
                        bi -- 更新门的偏置，维度为(n_a, 1)
                        Wc -- 第一个“tanh”的权值，维度为(n_a, n_a + n_x)
                        bc -- 第一个“tanh”的偏置，维度为(n_a, n_a + n_x)
                        Wo -- 输出门的权值，维度为(n_a, n_a + n_x)
                        bo -- 输出门的偏置，维度为(n_a, 1)
                        Wy -- 隐藏状态与输出相关的权值，维度为(n_y, n_a)
                        by -- 隐藏状态与输出相关的偏置，维度为(n_y, 1)
        
    返回：
        a -- 所有时间步的隐藏状态，维度为(n_a, m, T_x)
        y -- 所有时间步的预测值，维度为(n_y, m, T_x)
        caches -- 为反向传播的保存的元组，维度为（【列表类型】cache, x)）
    """
    
    # 初始化“caches”
    caches = []
    
    # 获取 xt 与 Wy 的维度信息
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wy"].shape
    
    # 使用0来初始化“a”、“c”、“y”
    a = np.zeros([n_a, m, T_x])
    c = np.zeros([n_a, m, T_x])
    y = np.zeros([n_y, m, T_x])
    
    # 初始化“a_next”、“c_next”
    a_next = a0
    c_next = np.zeros([n_a, m])
    
    # 遍历所有的时间步
    for t in range(T_x):
        # 更新下一个隐藏状态，下一个记忆状态，计算预测值，获取cache
        a_next, c_next, yt_pred, cache = lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
        
        # 保存新的下一个隐藏状态到变量a中
        a[:, :, t] = a_next
        
        # 保存预测值到变量y中
        y[:, :, t] = yt_pred
        
        # 保存下一个单元状态到变量c中
        c[:, :, t] = c_next
        
        # 把cache添加到caches中
        caches.append(cache)
    
    # 保存反向传播需要的参数
    caches = (caches, x)
    
    return a, y, c, caches

np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a, y, c, caches = lstm_forward(x, a0, parameters)
print("a[4][3][6] = ", a[4][3][6])
print("a.shape = ", a.shape)
print("y[1][4][3] =", y[1][4][3])
print("y.shape = ", y.shape)
print("caches[1][1[1]] =", caches[1][1][1])
print("c[1][2][1]", c[1][2][1])
print("len(caches) = ", len(caches))

a[4][3][6] =  0.17211776753291672
a.shape =  (5, 10, 7)
y[1][4][3] = 0.9508734618501101
y.shape =  (2, 10, 7)
caches[1][1[1]] = [ 0.82797464  0.23009474  0.76201118 -0.22232814 -0.20075807  0.18656139
  0.41005165]
c[1][2][1] -0.8555449167181982
len(caches) =  2

def rnn_cell_backward(da_next, cache):
    """
    实现基本的RNN单元的单步反向传播
    
    参数：
        da_next -- 关于下一个隐藏状态的损失的梯度。
        cache -- 字典类型，rnn_step_forward()的输出
        
    返回：
        gradients -- 字典，包含了以下参数：
                        dx -- 输入数据的梯度，维度为(n_x, m)
                        da_prev -- 上一隐藏层的隐藏状态，维度为(n_a, m)
                        dWax -- 输入到隐藏状态的权重的梯度，维度为(n_a, n_x)
                        dWaa -- 隐藏状态到隐藏状态的权重的梯度，维度为(n_a, n_a)
                        dba -- 偏置向量的梯度，维度为(n_a, 1)
    """
    # 获取cache 的值
    a_next, a_prev, xt, parameters = cache
    
    # 从 parameters 中获取参数
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]
    
    # 计算tanh相对于a_next的梯度.
    dtanh = (1 - np.square(a_next)) * da_next
    
    # 计算关于Wax损失的梯度
    dxt = np.dot(Wax.T,dtanh)
    dWax = np.dot(dtanh, xt.T)
    
    # 计算关于Waa损失的梯度
    da_prev = np.dot(Waa.T,dtanh)
    dWaa = np.dot(dtanh, a_prev.T)
    
    # 计算关于b损失的梯度
    dba = np.sum(dtanh, keepdims=True, axis=-1)
    
    # 保存这些梯度到字典内
    gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
    
    return gradients

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
b = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}

a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)

da_next = np.random.randn(5,10)
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)

gradients["dxt"][1][2] = -0.4605641030588796
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = 0.08429686538067718
gradients["da_prev"].shape = (5, 10)
gradients["dWax"][3][1] = 0.3930818739219304
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = -0.2848395578696067
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [0.80517166]
gradients["dba"].shape = (5, 1)

def rnn_backward(da, caches):
    """
    在整个输入数据序列上实现RNN的反向传播
    
    参数：
        da -- 所有隐藏状态的梯度，维度为(n_a, m, T_x)
        caches -- 包含向前传播的信息的元组
    
    返回：    
        gradients -- 包含了梯度的字典：
                        dx -- 关于输入数据的梯度，维度为(n_x, m, T_x)
                        da0 -- 关于初始化隐藏状态的梯度，维度为(n_a, m)
                        dWax -- 关于输入权重的梯度，维度为(n_a, n_x)
                        dWaa -- 关于隐藏状态的权值的梯度，维度为(n_a, n_a)
                        dba -- 关于偏置的梯度，维度为(n_a, 1)
    """
    # 从caches中获取第一个cache（t=1）的值
    caches, x = caches
    a1, a0, x1, parameters = caches[0]
    
    # 获取da与x1的维度信息
    n_a, m, T_x = da.shape
    n_x, m = x1.shape
    
    # 初始化梯度
    dx = np.zeros([n_x, m, T_x])
    dWax = np.zeros([n_a, n_x])
    dWaa = np.zeros([n_a, n_a])
    dba = np.zeros([n_a, 1])
    da0 = np.zeros([n_a, m])
    da_prevt = np.zeros([n_a, m])
    
    # 处理所有时间步
    for t in reversed(range(T_x)):
        # 计算时间步“t”时的梯度
        gradients = rnn_cell_backward(da[:, :, t] + da_prevt, caches[t])
        
        #从梯度中获取导数
        dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
        
        # 通过在时间步t添加它们的导数来增加关于全局导数的参数
        dx[:, :, t] = dxt
        dWax += dWaxt
        dWaa += dWaat
        dba += dbat
        
    #将 da0设置为a的梯度，该梯度已通过所有时间步骤进行反向传播
    da0 = da_prevt
    
    #保存这些梯度到字典内
    gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
    
    return gradients

np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)

print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)

gradients["dx"][1][2] = [-2.07101689 -0.59255627  0.02466855  0.01483317]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.31494237512664996
gradients["da0"].shape = (5, 10)
gradients["dWax"][3][1] = 11.264104496527777
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = 2.303333126579893
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [-0.74747722]
gradients["dba"].shape = (5, 1)

def lstm_cell_backward(da_next, dc_next, cache):
    """
    实现LSTM的单步反向传播
    
    参数：
        da_next -- 下一个隐藏状态的梯度，维度为(n_a, m)
        dc_next -- 下一个单元状态的梯度，维度为(n_a, m)
        cache -- 来自前向传播的一些参数
        
    返回：
        gradients -- 包含了梯度信息的字典：
                        dxt -- 输入数据的梯度，维度为(n_x, m)
                        da_prev -- 先前的隐藏状态的梯度，维度为(n_a, m)
                        dc_prev -- 前的记忆状态的梯度，维度为(n_a, m, T_x)
                        dWf -- 遗忘门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbf -- 遗忘门的偏置的梯度，维度为(n_a, 1)
                        dWi -- 更新门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbi -- 更新门的偏置的梯度，维度为(n_a, 1)
                        dWc -- 第一个“tanh”的权值的梯度，维度为(n_a, n_a + n_x)
                        dbc -- 第一个“tanh”的偏置的梯度，维度为(n_a, n_a + n_x)
                        dWo -- 输出门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbo -- 输出门的偏置的梯度，维度为(n_a, 1)
    """
    # 从cache中获取信息
    (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
    
    # 获取xt与a_next的维度信息
    n_x, m = xt.shape
    n_a, m = a_next.shape
    
    # 根据公式7-10来计算门的导数
    dot = da_next * np.tanh(c_next) * ot * (1 - ot)
    dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
    dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
    dft = (dc_next * c_prev + ot * (1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)
    
    # 根据公式11-14计算参数的导数
    concat = np.concatenate((a_prev, xt), axis=0).T
    dWf = np.dot(dft, concat)
    dWi = np.dot(dit, concat)
    dWc = np.dot(dcct, concat)
    dWo = np.dot(dot, concat)
    dbf = np.sum(dft,axis=1,keepdims=True)
    dbi = np.sum(dit,axis=1,keepdims=True)
    dbc = np.sum(dcct,axis=1,keepdims=True)
    dbo = np.sum(dot,axis=1,keepdims=True)
    
    
    # 使用公式15-17计算洗起来了隐藏状态、先前记忆状态、输入的导数。
    da_prev = np.dot(parameters["Wf"][:, :n_a].T, dft) + np.dot(parameters["Wc"][:, :n_a].T, dcct) +  np.dot(parameters["Wi"][:, :n_a].T, dit) + np.dot(parameters["Wo"][:, :n_a].T, dot)
        
    dc_prev = dc_next * ft + ot * (1 - np.square(np.tanh(c_next))) * ft * da_next
    
    dxt = np.dot(parameters["Wf"][:, n_a:].T, dft) + np.dot(parameters["Wc"][:, n_a:].T, dcct) +  np.dot(parameters["Wi"][:, n_a:].T, dit) + np.dot(parameters["Wo"][:, n_a:].T, dot)
    
    # 保存梯度信息到字典
    gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
                "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
    
    return gradients

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)

da_next = np.random.randn(5,10)
dc_next = np.random.randn(5,10)
gradients = lstm_cell_backward(da_next, dc_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)

gradients["dxt"][1][2] = 3.230559115109188
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = -0.06396214197109236
gradients["da_prev"].shape = (5, 10)
gradients["dc_prev"][2][3] = 0.7975220387970015
gradients["dc_prev"].shape = (5, 10)
gradients["dWf"][3][1] = -0.1479548381644968
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 1.0574980552259903
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = 2.3045621636876668
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.3313115952892109
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [0.18864637]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.40142491]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [0.25587763]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [0.13893342]
gradients["dbo"].shape = (5, 1)

def lstm_backward(da, caches):
    
    """
    实现LSTM网络的反向传播
    
    参数：
        da -- 关于隐藏状态的梯度，维度为(n_a, m, T_x)
        cachses -- 前向传播保存的信息
    
    返回：
        gradients -- 包含了梯度信息的字典：
                        dx -- 输入数据的梯度，维度为(n_x, m，T_x)
                        da0 -- 先前的隐藏状态的梯度，维度为(n_a, m)
                        dWf -- 遗忘门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbf -- 遗忘门的偏置的梯度，维度为(n_a, 1)
                        dWi -- 更新门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbi -- 更新门的偏置的梯度，维度为(n_a, 1)
                        dWc -- 第一个“tanh”的权值的梯度，维度为(n_a, n_a + n_x)
                        dbc -- 第一个“tanh”的偏置的梯度，维度为(n_a, n_a + n_x)
                        dWo -- 输出门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbo -- 输出门的偏置的梯度，维度为(n_a, 1)
        
    """

    # 从caches中获取第一个cache（t=1）的值
    caches, x = caches
    (a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
    
    # 获取da与x1的维度信息
    n_a, m, T_x = da.shape
    n_x, m = x1.shape
    
    # 初始化梯度
    dx = np.zeros([n_x, m, T_x])
    da0 = np.zeros([n_a, m])
    da_prevt = np.zeros([n_a, m])
    dc_prevt = np.zeros([n_a, m])
    dWf = np.zeros([n_a, n_a + n_x])
    dWi = np.zeros([n_a, n_a + n_x])
    dWc = np.zeros([n_a, n_a + n_x])
    dWo = np.zeros([n_a, n_a + n_x])
    dbf = np.zeros([n_a, 1])
    dbi = np.zeros([n_a, 1])
    dbc = np.zeros([n_a, 1])
    dbo = np.zeros([n_a, 1])
    
    # 处理所有时间步
    for t in reversed(range(T_x)):
        # 使用lstm_cell_backward函数计算所有梯度
        gradients = lstm_cell_backward(da[:,:,t],dc_prevt,caches[t])
        # 保存相关参数
        dx[:,:,t] = gradients['dxt']
        dWf = dWf+gradients['dWf']
        dWi = dWi+gradients['dWi']
        dWc = dWc+gradients['dWc']
        dWo = dWo+gradients['dWo']
        dbf = dbf+gradients['dbf']
        dbi = dbi+gradients['dbi']
        dbc = dbc+gradients['dbc']
        dbo = dbo+gradients['dbo']
    # 将第一个激活的梯度设置为反向传播的梯度da_prev。
    da0 = gradients['da_prev']

    # 保存所有梯度到字典变量内
    gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
                "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
    
    return gradients

np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a, y, c, caches = lstm_forward(x, a0, parameters)

da = np.random.randn(5, 10, 4)
gradients = lstm_backward(da, caches)

print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)

gradients["dx"][1][2] = [-0.00173313  0.08287442 -0.30545663 -0.43281115]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.09591150195400468
gradients["da0"].shape = (5, 10)
gradients["dWf"][3][1] = -0.0698198561274401
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 0.10237182024854774
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = -0.062498379492745226
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.04843891314443013
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [-0.0565788]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.15399065]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [-0.29691142]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [-0.29798344]
gradients["dbo"].shape = (5, 1)

import numpy as np
import random
import time
import cllm_utils

# 获取名称
data = open("dinos.txt", "r").read()

# 转化为小写字符
data = data.lower()

# 转化为无序且不重复的元素列表
chars = list(set(data))

# 获取大小信息
data_size, vocab_size = len(data), len(chars)

print(chars)
print("共计有%d个字符，唯一字符有%d个"%(data_size,vocab_size))

['w', 'l', 't', 'q', 'a', 'd', 'b', 'f', 'm', 'o', 'n', '\n', 'y', 'e', 'i', 'j', 'v', 's', 'h', 'u', 'r', 'x', 'c', 'g', 'p', 'z', 'k']
共计有19909个字符，唯一字符有27个

char_to_ix = {ch:i for i, ch in enumerate(sorted(chars))}
ix_to_char = {i:ch for i, ch in enumerate(sorted(chars))}

print(char_to_ix)
print(ix_to_char)

{'\n': 0, 'a': 1, 'b': 2, 'c': 3, 'd': 4, 'e': 5, 'f': 6, 'g': 7, 'h': 8, 'i': 9, 'j': 10, 'k': 11, 'l': 12, 'm': 13, 'n': 14, 'o': 15, 'p': 16, 'q': 17, 'r': 18, 's': 19, 't': 20, 'u': 21, 'v': 22, 'w': 23, 'x': 24, 'y': 25, 'z': 26}
{0: '\n', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}

def clip(gradients, maxValue):
    """
    使用maxValue来修剪梯度
    
    参数：
        gradients -- 字典类型，包含了以下参数："dWaa", "dWax", "dWya", "db", "dby"
        maxValue -- 阈值，把梯度值限制在[-maxValue, maxValue]内
        
    返回：
        gradients -- 修剪后的梯度
    """
    # 获取参数
    dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients['dby']
    
    # 梯度修剪
    for gradient in [dWaa, dWax, dWya, db, dby]:
        np.clip(gradient, -maxValue, maxValue, out=gradient)

    gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}
    
    return gradients

np.random.seed(3)
dWax = np.random.randn(5,3)*10
dWaa = np.random.randn(5,5)*10
dWya = np.random.randn(2,5)*10
db = np.random.randn(5,1)*10
dby = np.random.randn(2,1)*10
gradients = {"dWax": dWax, "dWaa": dWaa, "dWya": dWya, "db": db, "dby": dby}
gradients = clip(gradients, 10)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])

gradients["dWaa"][1][2] = 10.0
gradients["dWax"][3][1] = -10.0
gradients["dWya"][1][2] = 0.2971381536101662
gradients["db"][4] = [10.]
gradients["dby"][1] = [8.45833407]

np.random.seed(0)
p = np.array([0.1, 0.0, 0.7, 0.2])
index = np.random.choice([0, 1, 2, 3], p = p.ravel())

def sample(parameters, char_to_is, seed):
    """
    根据RNN输出的概率分布序列对字符序列进行采样
    
    参数：
        parameters -- 包含了Waa, Wax, Wya, by, b的字典
        char_to_ix -- 字符映射到索引的字典
        seed -- 随机种子
        
    返回：
        indices -- 包含采样字符索引的长度为n的列表。
    """
    
    # 从parameters 中获取参数
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    vocab_size = by.shape[0]
    n_a = Waa.shape[1]
    
    # 步骤1 
    ## 创建独热向量x
    x = np.zeros((vocab_size,1))
    
    ## 使用0初始化a_prev
    a_prev = np.zeros((n_a,1))
    
    # 创建索引的空列表，这是包含要生成的字符的索引的列表。
    indices = []
    
    # IDX是检测换行符的标志，我们将其初始化为-1。
    idx = -1
    
    # 循环遍历时间步骤t。在每个时间步中，从概率分布中抽取一个字符，
    # 并将其索引附加到“indices”上，如果我们达到50个字符，
    #（我们应该不太可能有一个训练好的模型），我们将停止循环，这有助于调试并防止进入无限循环
    counter = 0
    newline_character = char_to_ix["\n"]
    
    while (idx != newline_character and counter < 50):
        # 步骤2：使用公式1、2、3进行前向传播
        a = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b)
        z = np.dot(Wya, a) + by
        y = cllm_utils.softmax(z)
        
        # 设定随机种子
        np.random.seed(counter + seed)
        
        # 步骤3：从概率分布y中抽取词汇表中字符的索引
        idx = np.random.choice(list(range(vocab_size)), p=y.ravel())
        
        # 添加到索引中
        indices.append(idx)
        
        # 步骤4:将输入字符重写为与采样索引对应的字符。
        x = np.zeros((vocab_size,1))
        x[idx] = 1
        
        # 更新a_prev为a
        a_prev = a 
        
        # 累加器
        seed += 1
        counter +=1
    
    if(counter == 50):
        indices.append(char_to_ix["\n"])
    
    return indices
        

np.random.seed(2)
_, n_a = 20, 100
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}


indices = sample(parameters, char_to_ix, 0)
print("Sampling:")
print("list of sampled indices:", indices)
print("list of sampled characters:", [ix_to_char[i] for i in indices])

Sampling:
list of sampled indices: [12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 0]
list of sampled characters: ['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', '\n']

def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):
    """
    执行训练模型的单步优化。
    
    参数：
        X -- 整数列表，其中每个整数映射到词汇表中的字符。
        Y -- 整数列表，与X完全相同，但向左移动了一个索引。
        a_prev -- 上一个隐藏状态
        parameters -- 字典，包含了以下参数：
                        Wax -- 权重矩阵乘以输入，维度为(n_a, n_x)
                        Waa -- 权重矩阵乘以隐藏状态，维度为(n_a, n_a)
                        Wya -- 隐藏状态与输出相关的权重矩阵，维度为(n_y, n_a)
                        b -- 偏置，维度为(n_a, 1)
                        by -- 隐藏状态与输出相关的权重偏置，维度为(n_y, 1)
        learning_rate -- 模型学习的速率
    
    返回：
        loss -- 损失函数的值（交叉熵损失）
        gradients -- 字典，包含了以下参数：
                        dWax -- 输入到隐藏的权值的梯度，维度为(n_a, n_x)
                        dWaa -- 隐藏到隐藏的权值的梯度，维度为(n_a, n_a)
                        dWya -- 隐藏到输出的权值的梯度，维度为(n_y, n_a)
                        db -- 偏置的梯度，维度为(n_a, 1)
                        dby -- 输出偏置向量的梯度，维度为(n_y, 1)
        a[len(X)-1] -- 最后的隐藏状态，维度为(n_a, 1)
    """
    
    # 前向传播
    loss, cache = cllm_utils.rnn_forward(X, Y, a_prev, parameters)
    
    # 反向传播
    gradients, a = cllm_utils.rnn_backward(X, Y, parameters, cache)
    
    # 梯度修剪，[-5 , 5]
    gradients = clip(gradients,5)
    
    # 更新参数
    parameters = cllm_utils.update_parameters(parameters,gradients,learning_rate)
    
    return loss, gradients, a[len(X)-1]
    

np.random.seed(1)
vocab_size, n_a = 27, 100
a_prev = np.random.randn(n_a, 1)
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
X = [12,3,5,11,22,3]
Y = [4,14,11,22,25, 26]

loss, gradients, a_last = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)
print("Loss =", loss)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("np.argmax(gradients[\"dWax\"]) =", np.argmax(gradients["dWax"]))
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
print("a_last[4] =", a_last[4])

Loss = 126.50397572165359
gradients["dWaa"][1][2] = 0.19470931534721306
np.argmax(gradients["dWax"]) = 93
gradients["dWya"][1][2] = -0.007773876032003657
gradients["db"][4] = [-0.06809825]
gradients["dby"][1] = [0.01538192]
a_last[4] = [-1.]

def model(data, ix_to_char, char_to_ix, num_iterations=3500, 
          n_a=50, dino_names=7,vocab_size=27):
    """
    训练模型并生成恐龙名字
    
    参数：
        data -- 语料库
        ix_to_char -- 索引映射字符字典
        char_to_ix -- 字符映射索引字典
        num_iterations -- 迭代次数
        n_a -- RNN单元数量
        dino_names -- 每次迭代中采样的数量
        vocab_size -- 在文本中的唯一字符的数量
    
    返回：
        parameters -- 学习后了的参数
    """
    
    # 从vocab_size中获取n_x、n_y
    n_x, n_y = vocab_size, vocab_size
    
    # 初始化参数
    parameters = cllm_utils.initialize_parameters(n_a, n_x, n_y)
    
    # 初始化损失
    loss = cllm_utils.get_initial_loss(vocab_size, dino_names)
    
    # 构建恐龙名称列表
    with open("dinos.txt") as f:
        examples = f.readlines()
    examples = [x.lower().strip() for x in examples]
    
    # 打乱全部的恐龙名称
    np.random.seed(0)
    np.random.shuffle(examples)
    
    # 初始化LSTM隐藏状态
    a_prev = np.zeros((n_a,1))
    
    # 循环
    for j in range(num_iterations):
        # 定义一个训练样本
        index = j % len(examples)
        X = [None] + [char_to_ix[ch] for ch in examples[index]] 
        Y = X[1:] + [char_to_ix["\n"]]
        
        # 执行单步优化：前向传播 -> 反向传播 -> 梯度修剪 -> 更新参数
        # 选择学习率为0.01
        curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters)
        
        # 使用延迟来保持损失平滑,这是为了加速训练。
        loss = cllm_utils.smooth(loss, curr_loss)
        
        # 每2000次迭代，通过sample()生成“\n”字符，检查模型是否学习正确
        if j % 2000 == 0:
            print("第" + str(j+1) + "次迭代，损失值为：" + str(loss))
            
            seed = 0
            for name in range(dino_names):
                # 采样
                sampled_indices = sample(parameters, char_to_ix, seed)
                cllm_utils.print_sample(sampled_indices, ix_to_char)
                
                # 为了得到相同的效果，随机种子+1
                seed += 1
            
            print("\n")
    return parameters

#开始时间
start_time = time.clock()

#开始训练
parameters = model(data, ix_to_char, char_to_ix, num_iterations=3500)

#结束时间
end_time = time.clock()

#计算时差
minium = end_time - start_time

print("执行了：" + str(int(minium / 60)) + "分" + str(int(minium%60)) + "秒")

/usr/local/lib/python3.7/site-packages/ipykernel_launcher.py:2: DeprecationWarning: time.clock has been deprecated in Python 3.3 and will be removed from Python 3.8: use time.perf_counter or time.process_time instead
  

第1次迭代，损失值为：23.087336085484605
Nkzxwtdmfqoeyhsqwasjkjvu
Kneb
Kzxwtdmfqoeyhsqwasjkjvu
Neb
Zxwtdmfqoeyhsqwasjkjvu
Eb
Xwtdmfqoeyhsqwasjkjvu


第2001次迭代，损失值为：27.884160491415773
Liusskeomnolxeros
Hmdaairus
Hytroligoraurus
Lecalosapaus
Xusicikoraurus
Abalpsamantisaurus
Tpraneronxeros


执行了：0分4秒

/usr/local/lib/python3.7/site-packages/ipykernel_launcher.py:8: DeprecationWarning: time.clock has been deprecated in Python 3.3 and will be removed from Python 3.8: use time.perf_counter or time.process_time instead
  

#开始时间
start_time = time.clock()

from keras.callbacks import LambdaCallback
from keras.models import Model, load_model, Sequential
from keras.layers import Dense, Activation, Dropout, Input, Masking
from keras.layers import LSTM
from keras.utils.data_utils import get_file
from keras.preprocessing.sequence import pad_sequences
from shakespeare_utils import *
import sys
import io

#结束时间
end_time = time.clock()

#计算时差
minium = end_time - start_time

print("执行了：" + str(int(minium / 60)) + "分" + str(int(minium%60)) + "秒")

执行了：0分0秒

/usr/local/lib/python3.7/site-packages/ipykernel_launcher.py:2: DeprecationWarning: time.clock has been deprecated in Python 3.3 and will be removed from Python 3.8: use time.perf_counter or time.process_time instead
  
/usr/local/lib/python3.7/site-packages/ipykernel_launcher.py:15: DeprecationWarning: time.clock has been deprecated in Python 3.3 and will be removed from Python 3.8: use time.perf_counter or time.process_time instead
  from ipykernel import kernelapp as app

print_callback = LambdaCallback(on_epoch_end=on_epoch_end)

model.fit(x, y, batch_size=128, epochs=1, callbacks=[print_callback])

Epoch 1/1
31412/31412 [==============================] - 55s 2ms/step - loss: 1.9529

Out[181]:

<keras.callbacks.callbacks.History at 0x1839d0ad0>

# 运行此代码尝试不同的输入，而不必重新训练模型。
generate_output() #博主在这里输入hello

Write the beginning of your poem, the Shakespeare machine will complete it. Your input is: hello


Here is your poem: 

helloto sweet,
which swich to reabustude thing,, the is betorncy thee,
loiky flumswringre wiste wyoing grows thee,
who be whete, or you dedires to innains asos,
and doll me which fartore ang pane.



twan be thou sin the whech beour whoul tame:
for the pose the dodfre me deloveds grear.

i amsind (nout in ay pruise, and hit tind drestill cills,
i sack which the grint of real part'st bants thise is dowd

#------------用于绘制模型细节，可选--------------#
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model

%matplotlib inline
plot_model(model, to_file='shakespeare.png')
SVG(model_to_dot(model).create(prog='dot', format='svg'))
#------------------------------------------------#

input_3: InputLayer

lstm_5: LSTM

dropout_3: Dropout

lstm_6: LSTM

dropout_4: Dropout

dense_3: Dense

activation_3: Activation

from keras.models import load_model, Model
from keras.layers import Dense, Activation, Dropout, Input, LSTM, Reshape, Lambda, RepeatVector
from keras.initializers import glorot_uniform
from keras.utils import to_categorical
from keras.optimizers import Adam
from keras import backend as K
import numpy as np
import IPython

from music21 import *
from grammar import *
from qa import *
from preprocess import * 
from music_utils import *
from data_utils import *

X, Y, n_values, indices_values = load_music_utils()
print('shape of X:', X.shape)
print('number of training examples:', X.shape[0])
print('Tx (length of sequence):', X.shape[1])
print('total # of unique values:', n_values)
print('Shape of Y:', Y.shape)

shape of X: (60, 30, 90)
number of training examples: 60
Tx (length of sequence): 30
total # of unique values: 90
Shape of Y: (30, 60, 90)

n_a = 64

#reshapor = Reshape((1, 78))                        #2.B
reshapor = Reshape((1, 90))    
LSTM_cell = LSTM(n_a, return_state = True, input_shape=(3, ))        #2.C
densor = Dense(n_values, activation='softmax')    #2.D

def djmodel(Tx, n_a, n_values):
    """
    实现这个模型
    
    参数：
        Tx -- 语料库的长度
        n_a -- 激活值的数量
        n_values -- 音乐数据中唯一数据的数量
        
    返回：
        model -- Keras模型实体
    """
    # 定义输入数据的维度
    X = Input((Tx, n_values))
    
    # 定义a0, 初始化隐藏状态
    a0 = Input(shape=(n_a,),name="a0")
    c0 = Input(shape=(n_a,),name="c0")
    a = a0
    c = c0
    
    # 第一步：创建一个空的outputs列表来保存LSTM的所有时间步的输出。
    outputs = []
    
    # 第二步：循环
    for t in range(Tx):
        ## 2.A：从X中选择第“t”个时间步向量
        x = Lambda(lambda x:X[:, t, :])(X)
        
        ## 2.B：使用reshapor来对x进行重构为(1, n_values)
        x = reshapor(x)
        
        ## 2.C：单步传播
        a, _, c = LSTM_cell(x, initial_state=[a, c])
        
        ## 2.D：使用densor()应用于LSTM_Cell的隐藏状态输出
        out = densor(a)
        
        ## 2.E：把预测值添加到"outputs"列表中
        outputs.append(out)
        
    # 第三步：创建模型实体
    model = Model(inputs=[X, a0, c0], outputs=outputs)
    
    return model

# 获取模型，这里Tx=30, n_a=64，n_values=78
#model = djmodel(Tx = 30 , n_a = 64, n_values = 78)
model = djmodel(Tx = 30 , n_a = 64, n_values = 90)

# 编译模型，我们使用Adam优化器与分类熵损失。
opt = Adam(lr=0.01, beta_1=0.9, beta_2=0.999, decay=0.01)
model.compile(optimizer=opt, loss='categorical_crossentropy', metrics=['accuracy'])

# 初始化a0和c0，使LSTM的初始状态为零。
m = 60
a0 = np.zeros((m, n_a))
c0 = np.zeros((m, n_a))

import time

#开始时间
start_time = time.clock()

#开始拟合
model.fit([X, a0, c0], list(Y), epochs=100)

#结束时间
end_time = time.clock()

#计算时差
minium = end_time - start_time

print("执行了：" + str(int(minium / 60)) + "分" + str(int(minium%60)) + "秒")

#def music_inference_model(LSTM_cell, densor, n_values = 78, n_a = 64, Ty = 100):
def music_inference_model(LSTM_cell, densor, n_values = 90, n_a = 64, Ty = 100):
    """
    参数：
        LSTM_cell -- 来自model()的训练过后的LSTM单元，是keras层对象。
        densor -- 来自model()的训练过后的"densor"，是keras层对象
        n_values -- 整数，唯一值的数量
        n_a -- LSTM单元的数量
        Ty -- 整数，生成的是时间步的数量
        
    返回：
        inference_model -- Kears模型实体
    """
    
    # 定义模型输入的维度
    x0 = Input(shape=(1,n_values))
    
    # 定义s0，初始化隐藏状态
    a0 = Input(shape=(n_a,),name="a0")
    c0 = Input(shape=(n_a,),name="c0")
    a = a0
    c = c0
    x = x0
    
    # 步骤1：创建一个空的outputs列表来保存预测值。
    outputs = []
    
    # 步骤2：遍历Ty，生成所有时间步的输出
    for t in range(Ty):
        
        # 步骤2.A：在LSTM中单步传播
        a, _, c = LSTM_cell(x, initial_state=[a, c])
        
        # 步骤2.B：使用densor()应用于LSTM_Cell的隐藏状态输出
        out = densor(a)
        
        # 步骤2.C：预测值添加到"outputs"列表中
        outputs.append(out)
        
        # 根据“out”选择下一个值，并将“x”设置为所选值的一个独热编码，
        # 该值将在下一步作为输入传递给LSTM_cell。我们已经提供了执行此操作所需的代码
        x = Lambda(one_hot)(out)
        
    # 创建模型实体
    inference_model = Model(inputs=[x0, a0, c0], outputs=outputs)
    
    return inference_model

# 获取模型实体，模型被硬编码以产生50个值
#inference_model = music_inference_model(LSTM_cell, densor, n_values = 78, n_a = 64, Ty = 50)
inference_model = music_inference_model(LSTM_cell, densor, n_values = 78, n_a = 64, Ty = 50)

#创建用于初始化x和LSTM状态变量a和c的零向量。
#x_initializer = np.zeros((1, 1, 78))
x_initializer = np.zeros((1, 1, 78))
a_initializer = np.zeros((1, n_a))
c_initializer = np.zeros((1, n_a))

Predicting new values for different set of chords.
Generated 51 sounds using the predicted values for the set of chords ("1") and after pruning
Generated 50 sounds using the predicted values for the set of chords ("2") and after pruning
Generated 51 sounds using the predicted values for the set of chords ("3") and after pruning
Generated 51 sounds using the predicted values for the set of chords ("4") and after pruning
Generated 50 sounds using the predicted values for the set of chords ("5") and after pruning
Your generated music is saved in output/my_music.midi

results, indices = predict_and_sample(inference_model, x_initializer, a_initializer, c_initializer)
print("np.argmax(results[12]) =", np.argmax(results[12]))
print("np.argmax(results[17]) =", np.argmax(results[17]))
print("list(indices[12:18]) =", list(indices[12:18]))

np.argmax(results[12]) = 71
np.argmax(results[17]) = 54
list(indices[12:18]) = [array([71], dtype=int64), array([12], dtype=int64), array([24], dtype=int64), array([57], dtype=int64), array([64], dtype=int64), array([54], dtype=int64)]

out_stream = generate_music(inference_model)

Predicting new values for different set of chords.
Generated 51 sounds using the predicted values for the set of chords ("1") and after pruning
Generated 50 sounds using the predicted values for the set of chords ("2") and after pruning
Generated 51 sounds using the predicted values for the set of chords ("3") and after pruning
Generated 51 sounds using the predicted values for the set of chords ("4") and after pruning
Generated 50 sounds using the predicted values for the set of chords ("5") and after pruning
Your generated music is saved in output/my_music.midi

IPython.display.Audio('./data/30s_trained_model.mp3')