题目如下:?
advertising.csv文件是某商品的广告推广费用(单位为元)和销售额数据(单位为千元),其中每行代表每一周的广告推广费用(包含微信、微博和其他类型三种广告费用)和销售额。若在未来的某两周,将各种广告投放金额按如下分配,请预测对应的商品销售额:
(1)微信:100,微博:100,其他类型:100
(2)微信:200,微博:100,其他类型:50
一、线性回归概念
对于因变量y:
如果它和自变量x呈现y=ax+b关系 称为一元线性。
如果y与多个因素有关。即 y=a1*x1+a2*x2+...? 称为多元线性。
回归要做的就是根据已有x和y 找到a和b,拟合出这一条直线,预测新x所对应的y。
二、题目分析?
首先得到数据(使用pandas),然后画散点图(使用plt)观察三个因素对销量的影响。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression as lr
adv=pd.read_csv("advertising.csv")
#print(adv)
x=np.array(adv.wechat)
#x1=np.array(adv.weibo)
#x2=np.array(adv.others)
y=np.array(adv.sales)
plt.scatter(x,y)
plt.show()#得到wechat和sales的散点图
#发现只有wechat和sales有线性关系,所以是一元线性回归
? 画出三个要素对应的散点图。发现只有微信部分和销售额有明显线性关系。
??
?参考文章机器学习基础线性回归——预测网店的销售额_sjjsaaaa的博客-CSDN博客_线性回归法预测销售额
(上文使用了seaborn库,可以一下子呈现三个坐标轴)
所以本题采用一元线性回归处理(简化了处理)
三、最简单代码
?对于预测问题,我们可以直接调用sklearn.linear库,直接使用fit和predict函数。
具体学习如下(其中重点注意fit函数的参数):【机器学习】(一) 线性模型之Linear Regression_walk_power的博客-CSDN博客_linearregression函数
所以写出了非常简答的代码:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression as lr
adv=pd.read_csv("advertising.csv")#读取文档
#print(adv)
x=np.array(adv.wechat)获得x
#x1=np.array(adv.weibo)
#x2=np.array(adv.others)
y=np.array(adv.sales)获得销量y
plt.scatter(x,y)
plt.show()#得到wechat和sales的散点图
#发现只有wechat和sales有线性关系,所以是一元线性回归
x_train=x.reshape(-1,1)#reshape的作用是改变数据的类型
y_train=y.reshape(-1,1)#fit的参数要求是二维矩阵。
x_test=np.array([100])#测试数据直接使用wechat部分。
x_test=x_test.reshape(-1,1)
model=lr()#直接调用库,创建了model
model.fit(x_train,y_train)
y_pred=model.predict(x_test)
print(y_pred)
运行结果如下:
 ?
?
四、线性回归建模
只是调用库来建模的话意义不大,下面我们自己来创建这个模型,即自己找到适合的a和b。
在机器学习中,y=ax+b可以专业的写成y=w*x+b。体现权重weight和bias偏置这两个概念。
首先了解一些基本知识:
1.误差函数:
在最小二乘法中,均方误差函数的数学表达式,刻画的是每个点的y和拟合出来的直线y撇的差距:
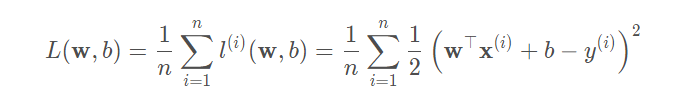 ?
?
均方误差函数(MSE)代码如下
def loss_function(X,y,weight,bias)
y_hat=weight*X+bias
loss=y_hat-y
cost=np.sum(loss**2)/2*len(X)
return cost2.梯度下降
对于上面这个loss_function函数,它可以表现成与w,b有关的一个三维图像,如下图:
 ?
?
我们的目的是找到图像的最低点,在该情况下的w和b拟合出的直线最为贴近。
一个朴素的处理思想是:先任意确定w和b得到loss,然后不断移动w,b,根据loss的高低来决定移动方向。
这个思想的具体计算方式是依靠导数。
理解梯度:在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率。梯度下降算法原理讲解——机器学习_Arrow and Bullet-CSDN博客_梯度下降法
对目前的X求导:
- 如果求导后梯度为正值,则说明L正在随着w增大而增大,应该减小w,以得到更小的损失。
- 如果求导后梯度为负值,则说明L正在随着w增大而减小,应该增大w,以得到更小的损失。
具体的求导方式:
y_hat = w*X + b # 这个是向量化运行实现的假设函数
loss = y_hat-y # 这是中间过程,求得的是假设函数预测的y和真正的y值间的差值
derivative_w = X.T.dot(loss)/len(X) # 对权重求导, len(X)是样本总数
derivative_b = sum(loss)*1/len(X) # 对偏置求导
知道了w该向哪个方向移动,下面就是怎么移动到最低点的问题。引入概念learnrate 学习率。
以w为例分析。已知当前的x导数为正,在w,y面 则应当向右移动,每次移动lr的长度,
如果lr较小,则得到x1对应y1为肯定比x对应的y更接近最低点。
如果lr较大,有可能越过了最低点,越过情况下y1有可能大于y,此时lr就太大了。
确定lr是这个程序模型拟合的重要一步。
在迭代多次(移动多次lr)以后,我们得到了最接近的w和b
def gradient(X,y,w,b):
for i in range(iter):#迭代iter次,每次移动lr步让w和b更接近拟合直线。
print(i)
print("现在损失是:",loss_function(X,y,w,b))
loss_history.append(loss_function(X,y,w,b))
loss=w*X+b-y
derivative_w=X.T.dot(loss)/len(X)#对权重求导
derivative_b=sum(loss)*1/len(X)#对偏置求导
print("权重导数:",derivative_w)
print("偏置导数:",derivative_b)
w=w-lr*derivative_w #改变w,将原来w-lr*der
print("现在w:",w)
b=b-lr*derivative_b #改变b,将原来w-lr*der
print("现在b:",b)
#plt.plot(X,w*X+b)#可以每次绘制一下直线拟合状况,直观一些。
return w,b整个程序的运行思路:先任意规定w,b,确定好iter,lr(这个可能有问题)
然后调用梯度下降函数。全部代码如下
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def loss_function(X,y,w,b):
loss=w*X+b-y
cost=np.sum(loss**2)/(2*len(X))
return cost
def gradient(X,y,w,b):
for i in range(iter):
print(i)
print("现在损失是:",loss_function(X,y,w,b))
loss_history.append(loss_function(X,y,w,b))
loss=w*X+b-y
derivative_w=X.T.dot(loss)/len(X)#对权重求导
derivative_b=sum(loss)*1/len(X)#对偏置求导
print("权重导数:",derivative_w)
print("偏置导数:",derivative_b)
w=w-lr*derivative_w #改变w,将原来w-lr*der
print("现在w:",w)
b=b-lr*derivative_b #改变b,将原来w-lr*der
print("现在b:",b)
#plt.plot(X,w*X+b)
return w,b
adv=pd.read_csv("advertising.csv")
X=np.array(adv.wechat)
y=np.array(adv.sales)
X_train=X.reshape(-1,1)
y_train=y.reshape(-1,1)#有了训练集的x和y
X_test=100
w=0.1
b=1
iter=100
lr=0.000002
loss_history=[]
plt.scatter(X_train,y_train)#绘制散点图
w1,b1=gradient(X,y,w,b)#最终得到w,b
plt.plot(X,w1*X+b1)
print("最后w,b 是:",w1,b1)
print(w1*X_test+b1)
plt.show()
如果发现在迭代过程中有Loss越来愈大的情况,说明选择的lr有问题,尝试调小步长。
选择的iter和lr不同,则最终的w和b有误差。
可以将迭代过程中的loss_history, weight_history, bias_history记录下来,最后查看一下。
运行结果:
 ?
?
"""下面是检验损失的
plt.plot(loss_history,'g--',label='Loss Curve')
plt.xlabel('Iterations') # x轴Label
plt.ylabel('Loss') # y轴Label
plt.legend() # 显示图例
plt.show() # 显示损失曲线
"""
将迭代中的损失记录下来,以图标形式呈现,体现下降趋势。

?
3.梯度下降的另一种处理
西瓜书上 对于线性回归有向量的表示方法,其中涉及X矩阵和w,b的运算,我们可以将wb看成一个新的变量theta,在拟合的时候变成对theta的处理。
 ?
?
?横坐标theta,纵坐标L。更加直观。具体参照上面的提到的博客。
五、其他完善
1.运用多元回归
基本思路是 将一元中的乘法变成点 乘W的T,修改部分如下
问题1.不知道三元的X怎么样和四元的W[w1,w2,w3,w4]点乘,所以舍去了b
? ? ? ?2.由于本例中第三个元素干扰实在太大,导致多元回归无法得到一个恰当的数值。
def loss_function(X, y, W): # 手工定义一个MSE均方误差函数
y_hat = X.dot(W.T) # 点积运算
loss = y_hat.reshape((len(y_hat),1))-y # 中间过程,求出当前W和真值的差值
cost = np.sum(loss**2)/(2*len(X)) # 这是均方误差函数的代码实现
return cost # 返回当前模型的均方误差值
def gradient_descent(X, y, W, lr, iter): # 定义一个实现梯度下降的函数
for i in range(iter): # 进行梯度下降的迭代,就是下多少级台阶
print(i)
print("现在损失是:",loss_function(X,y,W))
y_hat=X.dot(W.T)
#print("y_hat",y_hat)
loss=y_hat-y
#print("loss",loss)
derivate_W=X.T.dot(loss)/(2*len(W))
derivate_W=derivate_W.reshape(len(W))
#print("W导数是",derivate_W)
W=W-lr*derivate_W
print("现在W是",W)
return W2.数据的归一化。用来突出数据的特征,本次没有使用,这部分将在以后学习。
六、总结和反思
1.上面的三种处理方式,最后得到的预测值还是有较大差异,需要研究学习率和循环次数的一个更适合的数值。可以考虑用while循环将误差值控制到一个范围。
2.思考更简便的建立回归模型,思考后面两个元素是否真的没办法用到。
3.再深入了解一下梯度下降的相关内容。