[人工智能]深入理解交叉熵损失函数

前言

本文参照torch.nn.CrossEntropyLoss()说明文档¹，从原理和实现细节上对交叉熵损失进行深入理解。

一、交叉熵

1.1 交叉熵的定义

假设X是离散型随机变量，$p(x)、q(x)$为X的两个概率分布，交叉熵的定义如下：
$$H(q,p)=?\sum _{x}q(x)logp(x)$$
交叉熵可以用来衡量两分布之间的相似程度。 交叉熵越小，$p、q$两分布越相似，当$p=q$时，$H(p,q)$达到最小。

1.2 交叉熵损失

在分类问题中，交叉熵损失(Cross Entropy Loss)的定义为：
$$l(y,\hat{y})=?\sum _{j=1}^q{y}_{j}log\hat{y}$$
式中，$y$为样本的类别标签（长度为$q$的one-hot编码向量；$\hat{y}$为模型预测的输出概率。

二、最大似然估计

似然性：已知总体的分布函数的形式，根据已观察事件发生的概率估计模型分布函数的参数。²
概率：在已知总体分布函数的情况下，预测接下来某事件发生的概率。

2.1 似然函数

若总体X属于离散型，其分布律为 P { X = x } = p ( x ; θ ) , θ ∈ Θ P\{X=x\}=p(x;\theta),\theta\in \Theta P{X=x}=p(x;θ),θ∈Θ的形式已知，$\theta$为待估计参数，$\Theta$为$\theta$可能的取值范围。
假设$x_1,x_2,x_3,...,x_n$是对应于样本$X_1,X_2,X_3,...,X_n$的样本值，事件$X_1=x_1,X_2=x_2,X_3=x_3,...,X_n=x_n$发生的概率为：
$$L(\theta )=L(x_1,x_2,x_3,...,x_n;\theta )=\prod _{i=1}^{n}p(x_i;\theta )$$
式中，$p(x_i;\theta )$为事件$X_i=x_i$发生的概率。 $L(\theta )$随$\theta$的取值变化，称为样本的似然函数。

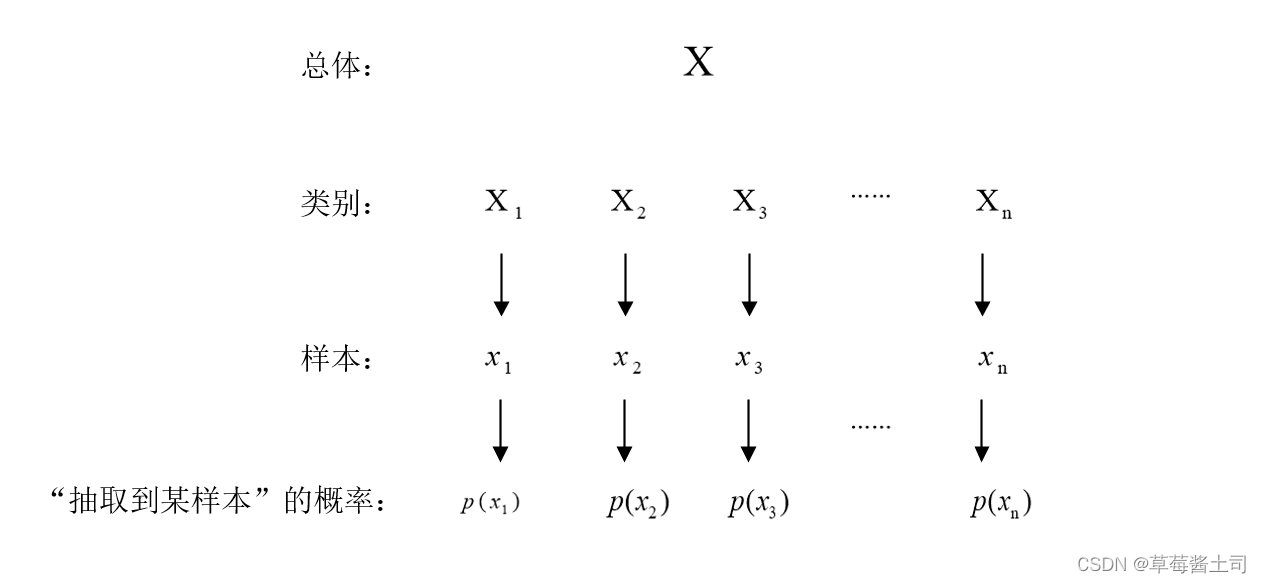
给出示意图方便理解：似然函数$L(\theta )$为事件 { X 1 = x 1 , X 2 = x 2 , X 3 = x 3 , . . . , X n = x n } \{X_1=x_1, X_2=x_2, X_3=x_3,...,X_n=x_n\} {X1?=x1?,X2?=x2?,X3?=x3?,...,Xn?=xn?}发生的概率。

2.2 最大似然估计

基本思想：固定样本观察值$x_1,x_2,x_3,...,x_n$，在$\theta$取值的可能范围内挑选使似然函数取得最大值的估计$\hat{\theta }$，即：
$$L(x_1,x_2,...,x_n;\hat{\theta })=\underset{\theta \in \Theta }{\max }L(x_1,x_2,...,x_n;\theta )$$
得到的参数估计$\hat{\theta }$与样本值$x_1,x_2,...,x_n$有关，记为$\hat{\theta }(x_1,x_2,...,x_n)$，称为参数$\theta$的最大似然估计值。

2.3 分类问题中的最大似然估计

假设为$K$分类问题，已知$n$个样本，对模型参数$p(x^{(i)},y^{(i)})$进行估计，则似然函数为：
$$L((x^{(i)},y^{(i)};p)=\prod _{i=1}^n\prod _{k=1}^K{p}^{y(k)}$$
通常优化问题为取最小值而非最大值，因此最大化似然函数可以转化为最小化负对数似然函数，负对数似然(negative likelihood)函数为：
$$?logL((x^{(i)},y^{(i)};p)=?\sum _{i=1}^n\sum _{k=1}^{K}y(k)log{p}_k$$
对照1.2节交叉熵损失函数的定义可知：最小化交叉熵损失函数和最小化负对数似然函数在公式上是等价的。
所以，可以从最大化样本似然的角度理解分类模型选用交叉熵作为损失函数。

三、交叉熵损失函数的实现

torch.nn.CrossEntropyLoss()说明文档中提到：

Note that this case is equivalent to the combination of LogSoftmax and NLLLoss.

Pytorch中log_softmax的实现已在博客³中详细讲述。
这里，主要通过代码理解负对数似然与交叉熵之间的联系（参考⁴)。

3.1 负对数似然损失函数(Negative Log Likelihood Loss)

负对数似然损失函数的定义：
$$nllloss=?\frac{1}{N}\sum _{i=1}^N{y}_{i}log\hat{y}=?\frac{1}{N}\sum _{i=1}^N{y}_i(logsoftmax)$$
式中，$N$为样本数量，$y_i$为one-hot编码后的真实样本标签，$\hat{y}$为模型的输出概率向量。

>>> import torch
>>> import torch.nn.functional as F
>>> import torch.nn as nn 
>>> X = torch.randn(5, 5)  # 创建5*5的样本（样本数量=5，5分类问题）
>>> label = torch.tensor([0, 2, 3, 4, 1])  # 5个样本的真实标签
>>> label_one_hot = F.one_hot(label).float()
>>> P = F.log_softmax(X, dim=1)  # 将输出转化为概率（这里做了防溢出处理）
'''自行实现nll loss'''
>>> nllloss = -torch.sum(label_one_hot * P) / label.shape[0] 
tensor(1.9052)
'''调用pytorch API 求负对数似然损失'''
>>> nllloss_1 = F.nll_loss(P, label) # 不需要对标签作one-hot编码处理
tensor(1.9052)
'''调用pytorch API 求交叉熵损失'''
>>> cross_entropy_loss = F.cross_entropy(X, label)
tensor(1.9052)

最终的执行结果是一致的。

3.2 自行实现CrossEntropyLoss函数

最后给出自行实现的代码：

'''自定义log-softmax函数，对模型输出作规范化校准并防止溢出'''
def log_softmax(X):
	c, _ = torch.max(X, dim=1, keepdim=True)
	log_sum_exp = c + torch.log(torch.sum(torch.exp(X - c), dim=1, keepdim=True))
	return X - log_sum_exp

'''自定义负对数似然函数'''
def nll_loss(P_k, label):
	label_one_hot = F.one_hot(label)
	return -torch.sum(label_one_hot * P_k) / label.shape[0] # 这里对所有样本取均值（因为cross_entropy默认'reduction=mean')
>>> X = torch.randn(5, 5)
>>> label = torch.tensor([0,2,3,4,1])
>>> nll_loss(log_softmax(X), label) == F.cross_entropy(X, label)
tensor(True)

最终的输出结果为True，说明torch.nn.CrossEntropy()的实现过程与自定义的实现是一致的。