[人工智能] 一起动手学数据分析 task05 模型搭建和评估

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 一起动手学数据分析 task05 模型搭建和评估 -> 正文阅读

[人工智能]一起动手学数据分析 task05 模型搭建和评估

载入数据

我们在前几个次学习中，学习了对数据本身的一系列处理。这一章的主要内容是使用数据，进行建模和评估。
我们这里使用的是泰坦尼克号的数据集，那么我们这次的目的就是，完成泰坦尼克号存活预测这个任务。

引入所需数据包

其他包都在以前的学习中讲解过什么用途。from IPython.display import Image是用来显示图像的包。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import Image

#图表直接显示在行运行块内
%matplotlib inline

 # 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
 # 用来正常显示负号
plt.rcParams['axes.unicode_minus'] = False 
 # 设置输出图像大小
plt.rcParams['figure.figsize'] = (10, 6)

载入训练数据集：

train = pd.read_csv('train.csv')
train.head()

在这里插入图片描述

数据清洗和处理

缺失值填充:
将所有缺失的Cabin填为NA
将所有缺失的Embarked填为S

# 对分类变量进行填充
train['Cabin'] = train['Cabin'].fillna('NA')
train['Embarked'] = train['Embarked'].fillna('S')

将所有缺失的Age填为其平均值

# 对连续变量进行填充
train['Age'] = train['Age'].fillna(train['Age'].mean())

# 检查缺失值比例
train.isnull().sum().sort_values(ascending=False)

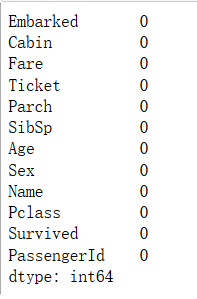
在这里插入图片描述
从图中可知，全部缺失均填充完毕。

编码分类变量:

# 取出所有的输入特征
data = train[['Pclass','Sex','Age','SibSp','Parch','Fare', 'Embarked']]

# 进行虚拟变量转换
data = pd.get_dummies(data)
data.head()

在这里插入图片描述
我们可以看到所需自变量数据全部提取出来，并清洗完毕了。

【扩展】

get_dummies ：用于one-hot编码。

保存：

data.to_csv('clear_data.csv')

读取清洗过的数据集：

#读取清洗过的数据集
data = pd.read_csv('clear_data.csv')
data.head()

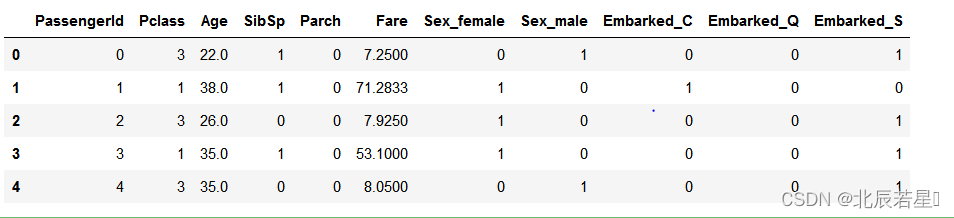
在这里插入图片描述
这两个数据集中的区别是，第二个数据进行了数据清洗和处理提取出了我们所要分析的特征，且缺少了Survied特征。

3.1 模型搭建

· 处理完前面的数据我们就得到建模数据，下一步是选择合适模型
· 在进行模型选择之前我们需要先知道数据集最终是进行监督学习还是无监督学习（主要区别是数据有无标签，监督学习有标签，无监督学习无标签），在这里是无监督学习，因为我们的清洗过后的数据集并没有加上存活的列。
· 除了根据我们任务来选择模型外，还可以根据数据样本量以及特征的稀疏性来决定
· 刚开始我们一般先尝试使用一个基本的模型来作为其baseline，进而再训练其他模型做对比，最终选择泛化能力或性能比较好的模型

建模一般不是自己从零开始搭建，而是借助了sklearn库来进行辅助的搭建。
下面是课程提供的sklearn模型算法选择路径图。
在这里插入图片描述

【思考】

数据拟合：即曲线拟合，把数据透过数学方法带入一条数式的表示方式。需要避免数据过拟合，导致异常值影响模型训练。

任务一：切割训练集和测试集

这里使用留出法划分数据集。将数据集分为自变量和因变量，并按比例切割训练集和测试集(一般测试集的比例有30%、25%、20%、15%和10%)，之后使用分层抽样和设置随机种子以便结果能复现。

【思考】

划分数据集的方法：
1.留出法是直接将数据集 D 划分为两个互斥的集合，其中一个集合作为训练集 S，另一个作为测试集 T。我们需要注意的是在划分的时候要尽可能保证数据分布的一致性，即避免因数据划分过程引入额外的偏差而对最终结果产生影响。
2.交叉验证法 k折交叉验证：通常将数据集 D 分为 k 份，其中的 k-1 份作为训练集，剩余的那一份作为测试集，这样就可以获得 k 组训练/测试集，可以进行 k 次训练与测试，最终返回的是 k 个测试结果的均值。这里数据集的划分依然是依据分层采样的方式来进行。对于交叉验证法，其 k 值的选取往往决定了评估结果的稳定性和保真性，通常 k 值选取 10。
3.自助法我们每次从数据集D中取一个样本作为训练集中的元素，然后把该样本放回，重复该行为 m 次，这样我们就可以得到大小为m的训练集，在这里面有的样本重复出现，有的样本则没有出现过，我们把那些没有出现过的样本作为测试集。

分层抽样好处：
1、如果层内的测量具有较低的标准偏差（与总体中的总体标准偏差相比），则分层会产生较小的估计误差。
2、对于许多数据集来说，当被分组到层中时，测量变得更易于管理和/或更便宜。
3、当需要对总体中的组进行总体参数估计时，分层抽样保证我们从感兴趣的层中获得了足够的样本。

在这个任务中，切割数据集是为了后续能评估模型泛化能力。 sklearn中切割数据集的方法为train_test_split，查看函数文档可以在jupyter notebook里面使用train_test_split后回车即可看到，分层和随机种子在参数里寻找。

引入切割函数的库：

from sklearn.model_selection import train_test_split

设置自变量x和因变量y：

# x是清洗好的数据，y是我们要预测的存活数据'Survived'
x = data
y = train['Survived']

切割数据集：

# 对数据集进行切割
x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y, random_state=0)

其中，x_train,x_test, y_train, y_test =train_test_split(train_data,train_target,test_size=0.4, random_state=0,stratify=y_train)

train_data：所要划分的样本特征集

train_target：所要划分的样本结果

test_size：样本占比，如果是整数的话就是样本的数量

random_state：是随机数的种子。其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。

stratify：按某一列进行分层采样，使数据分布均匀。
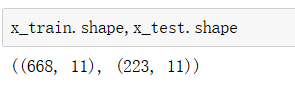
在这里插入图片描述
进行查看，我们可以得知分层之后的训练集有668行，测试集有223行，即是默认的取其中的25%。

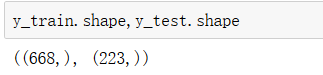
y同样如此划分的。

【拓展】

将random_state设置数值的原因是可以使结果进行复现，如果用0，则无法进复现。

【思考】

切割数据集的时候不用进行随机选取情况：在数据集本身已经是随机处理之后的情况下，或者说数据集非常大，使得内部已经足够随机了。

任务二：模型创建

创建基于线性模型的分类模型（逻辑回归）
创建基于树的分类模型（决策树、随机森林）
分别使用这些模型进行训练，分别的到训练集和测试集的得分
查看模型的参数，并更改参数值，观察模型变化

提示

逻辑回归不是回归模型而是分类模型，不要与LinearRegression混淆
随机森林其实是决策树集成为了降低决策树过拟合的情况
线性模型所在的模块为sklearn.linear_model
树模型所在的模块为sklearn.ensemble

我们可以先对结果进行观察：
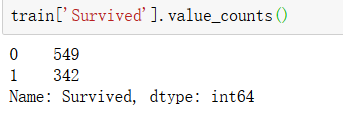
在这里插入图片描述

【扩展】

我们会发现存活人数和死亡人数不算非常失衡，我们可以不利用sample_weight来进行平衡建模，采用默认值。

导入所需函数：

from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier

逻辑回归：

# 逻辑回归模型
lr = LogisticRegression().fit(X_train, y_train)

其中，LogisticRegression()是建立模型，fit(X_train, y_train)是用X_train, y_train训练模型。

进行得分评判：

# 查看训练集和测试集score值
print("训练集得分: {:.2f}".format(lr.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(lr.score(X_test, y_test)))

.2f是指两位浮点数。
在这里插入图片描述

LogisticRegression()中，penalty参数用来正则化，防止过拟合；C参数越小正则化越强，模型越简单，C默认为1
进行C参数的尝试：

# 调整参数C后的逻辑回归模型
lr1 = LogisticRegression(C=0.01).fit(X_train, y_train)
print("训练集得分: {:.2f}".format(lr1.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(lr1.score(X_test, y_test)))

在这里插入图片描述
我们从评分可知，由于C过小，模型过于简单，开始欠拟合了。
我们设置大一点试试：

# 调整参数C后的逻辑回归模型
lr1 = LogisticRegression(C=1000).fit(X_train, y_train)
print("训练集得分: {:.2f}".format(lr1.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(lr1.score(X_test, y_test)))

在这里插入图片描述
模型复杂度加大后，我们可以看到，分数提高了。

我们再来试试平衡参数，即之前提到的weight。

# 调整参数C后的逻辑回归模型
lr2 = LogisticRegression(class_weight = 'balanced').fit(X_train, y_train)
print("训练集得分: {:.2f}".format(lr2.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(lr2.score(X_test, y_test)))

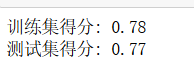
在这里插入图片描述
我们可以看到，分数反而下降了，说明这里不用平衡数据，数据较为均衡，再平衡反而影响得分。

建立随机森林分类模型并打分（减少噪声，提高模型稳定性）：

# 默认参数的随机森林分类模型
rfc = RandomForestClassifier().fit(X_train, y_train)
print("训练集得分: {:.2f}".format(rfc.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(rfc.score(X_test, y_test)))

在这里插入图片描述
接下来我们也进行一下调参，观察分数会发生什么样的变化：

【扩展】

1.数据不能过多，会产生欠拟合。
2.数据过多应设置树的深度。

首先，尝试n_estimators参数，即设置数据量。

# 改n_estimators参数的随机森林分类模型
rfc1 = RandomForestClassifier(n_estimators=100).fit(X_train, y_train)
print("训练集得分: {:.2f}".format(rfc1.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(rfc1.score(X_test, y_test)))

在这里插入图片描述
我们可以看到进行训练的数据的个数会影响模型的评分。

我们再来看看max_depth，即设置决策树最大深度。

# 改max_depth参数的随机森林分类模型
rfc2 = RandomForestClassifier(max_depth=5).fit(X_train, y_train)
print("训练集得分: {:.2f}".format(rfc2.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(rfc2.score(X_test, y_test)))

在这里插入图片描述
我们可以看到分数降低了，说明树的深度也不能太浅。

再看看bootstrap参数，即是否放回抽样。

# 改bootstrap参数的随机森林分类模型
rfc3 = RandomForestClassifier(bootstrap='false').fit(X_train, y_train)
print("训练集得分: {:.2f}".format(rfc3.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(rfc3.score(X_test, y_test)))

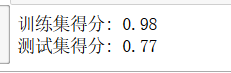
在这里插入图片描述

我们可以看到分数测试集有所提高。

oob_score参数（是否运用袋外数据）：

# 改oob_score参数的随机森林分类模型
rfc4 = RandomForestClassifier(oob_score='true').fit(X_train, y_train)
print("训练集得分: {:.2f}".format(rfc4.score(X_train, y_train)))
print("测试集得分: {:.2f}".format(rfc4.score(X_test, y_test)))

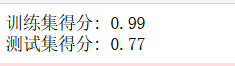
在这里插入图片描述
我们可以看到这个参数下，更改默认，可以将分数进行提高。

【思考】

线性模型可以进行分类任务，背后是怎么的数学关系：在这里插入图片描述
通过权重的不同可以进行相应的分类。
对于多分类问题，线性模型是怎么进行分类的：
本质还是二维分类，我们可以进行一步一步的二维分类，最后实现多分类的结果。

任务三：输出模型预测结果

我们这里使用逻辑回归模型进行输出：

#用逻辑回归进行预测标签
pred = lr.predict(X_train)

在这里插入图片描述
1代表存活，0代表死亡。

# 预测标签概率
pred_proba = lr.predict_proba(X_train)

在这里插入图片描述
图中，每一组第一个是预测死亡概率为0.1，存活概率为0.89，所以，最后预测标签为1，即判断为存活，以此类推。

【思考】

预测标签的概率对我们有什么帮助：可以让我们更直观的看到预测标签是如何得到的，概率是多少，有助于后期调参。

3.2 模型评估

模型评估是为了知道模型的泛化能力。
交叉验证（cross-validation）是一种评估泛化性能的统计学方法，它比单次划分训练集和测试集的方法更加稳定、全面。
在交叉验证中，数据被多次划分，并且需要训练多个模型。
最常用的交叉验证是 k 折交叉验证（k-fold cross-validation），其中 k 是由用户指定的数字，通常取 5 或 10。
准确率（precision）度量的是被预测为正例的样本中有多少是真正的正例。
召回率（recall）度量的是正类样本中有多少被预测为正类。
f-分数是准确率与召回率的调和平均。

任务一：交叉验证

用10折交叉验证来评估之前的逻辑回归模型
计算交叉验证精度的平均值

交叉验证在sklearn中的模块为sklearn.model_selection

from sklearn.model_selection import cross_val_score

cv 设置几折

lr = LogisticRegression()
scores = cross_val_score(lr, X_train, y_train, cv=10)

在这里插入图片描述
我们就在这里得到了10次交叉验证的评分。

求平均交叉验证分数：

# 平均交叉验证分数
print("平均交叉验证分数: {:.2f}".format(scores.mean()))

在这里插入图片描述
我们可得此次评估得分大约是0.8。

【思考】

k折越多的情况下会带来什么样的影响？
k折越多，评分越多，评估次数也越多，但相应的每一折的数据会减少，所以也不是折数越多越好。

任务二：混淆矩阵

计算二分类问题的混淆矩阵
计算精确率、召回率以及f-分数

混淆矩阵： 混淆矩阵也称误差矩阵，是表示精度评价的一种标准格式，用n行n列的矩阵形式来表示。混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。混淆矩阵中，永远是真实值在前，预测值在后。
二分类混淆矩阵如图所示：
在这里插入图片描述

如图是准确率 (Accuracy),精确度（Precision）,Recall,f-分数计算方法：
在这里插入图片描述

混淆矩阵的方法在sklearn中的sklearn.metrics模块
混淆矩阵需要输入真实标签和预测标签
精确率、召回率以及f-分数可使用classification_report模块

引入所需函数:

from sklearn.metrics import confusion_matrix

混淆矩阵(pred是前面输出的预测标签结果):

confusion_matrix(y_train, pred)

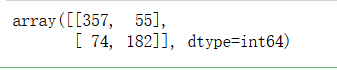
在这里插入图片描述
我们可以看到真的负类（预测正确死亡人数）有357个，真的正类（预测正确存活人数）有182个，其余预测错误。
引入所需函数，输出准确率 (Accuracy),精确度（Precision）,Recall,f-分数 （精确率和召回率的调和平均数，防止有时候它们有冲突的时候，也就是说需要设置权重来进行调整数据来判断是否准确） ：

from sklearn.metrics import classification_report
print(classification_report(y_train, pred))

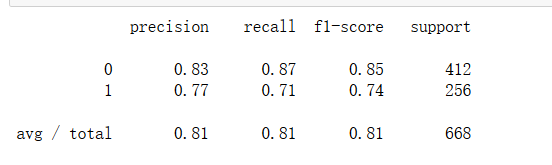
在这里插入图片描述
我们从图中可以看到调和平均数与召回率和精确度相差不大，说明两个之间没有太大冲突，没有极端情况。

任务三：ROC曲线

ROC曲线 ROC 曲线是根据一系列不同的二分类方式（分界值或决定阈），以真阳性率（灵敏度召回率）为纵坐标，假阳性率（1-特异度 FPR）为横坐标绘制的曲线。
在这里插入图片描述

【扩展】

在ROC曲线上，最接近于0的点是预测最好的点。
pos_label指定正类标签是哪一个。
decision_function：回归分类函数。

ROC曲线在sklearn中的模块为sklearn.metrics
ROC曲线下面所包围的面积越大越好

from sklearn.metrics import roc_curve
lrt = LogisticRegression().fit(X_test, y_test)
fpr,tpr,thresholds=roc_curve(y_test,lrt.decision_function(X_test))
fpr,tpr,thresholds

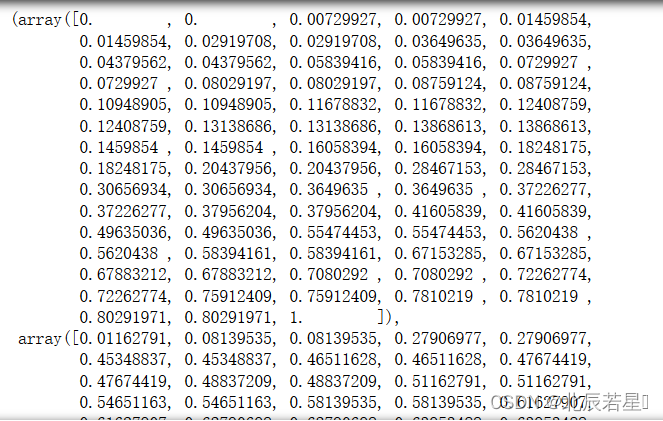
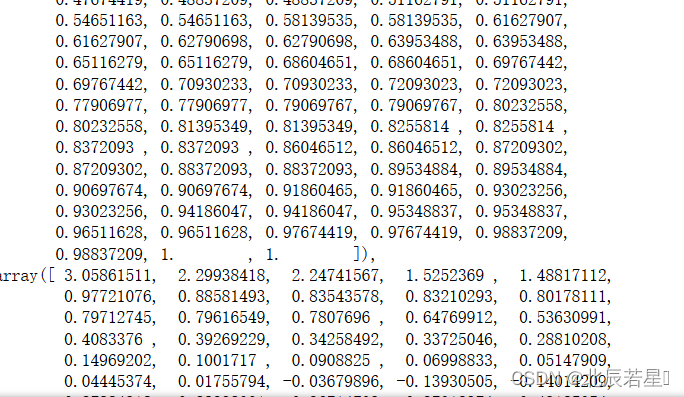
在这里插入图片描述

如图所示，分别返回了fpr（真阳性）,tpr（阈值）,thresholds（阈值）的值。

用plot画图：

plt.plot(fpr, tpr)
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")

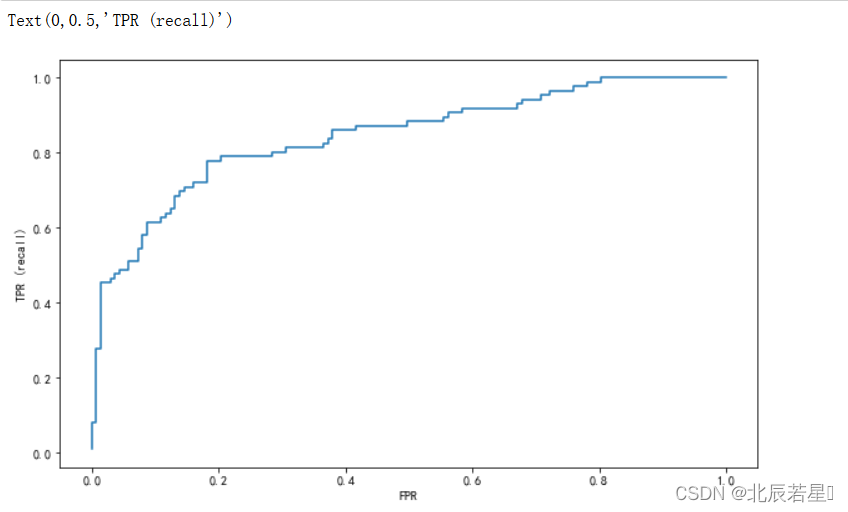
在这里插入图片描述

接下来，我们寻找最优点：
首先从阈值中求绝对值；然后用np.argmin函数找到最靠近0的点；然后进行保存。
下面我们用x来标出最优点：

plt.plot(fpr, tpr)
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'x')

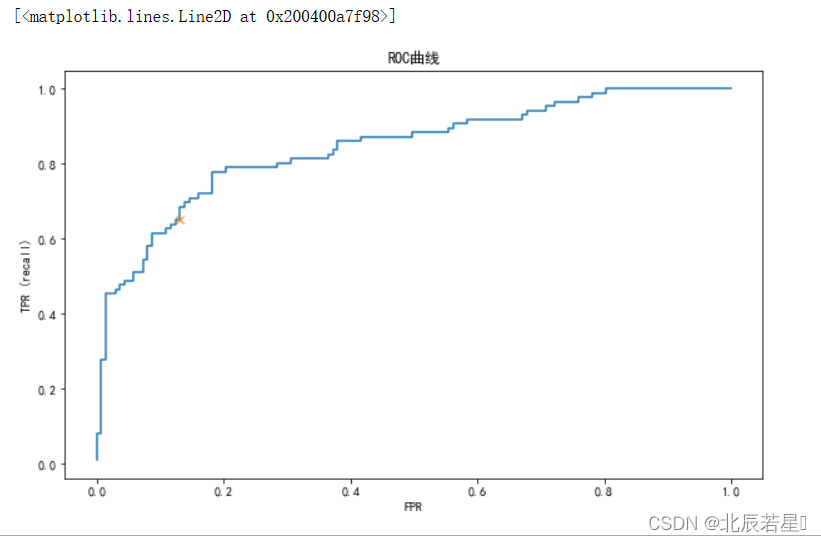
在这里插入图片描述

【扩展】

ROC曲线的主要作用：

(1)ROC曲线可以
便捷地查出一个分类器在某个阈值时对样本的识别能力。
(2)可以借助ROC曲线选择出某一模型最佳的预测界限值。ROC曲线越是靠近左上角，试验的FPR越高和FPR越低，即灵敏度越高，误判率越低，则预测模型的性能越好。可知ROC曲线上最靠近左上角的ROC曲线上的点其灵敏度和特异度之和最大，这个点被称为最佳临界点。
(3)ROC曲线可以用于比较两种或两种以上不同模型评估。在对同一数据集的两种或是两种模型进行比较时，可将各个模型的ROC曲线画到同一个ROC空间中(同一个坐标系中)，这样就可以直观的鉴别各种模型的优劣了。越靠近左上角的ROC曲线所代表的模型性能越好。