7 Introduction
underactuated robotics的第4,5,6章节是足式机器人建模和如何处理模型不确定性,因为对足式机器人的接触很少,先将这三个章节跳过去。先继续关注控制,规划和模型辨识。

7.1 Formulating control design as an optimization
最优控制是非常通用的框架,适用于各种机器人系统,通过构建goal 和constraints, 描述非常复杂的目标行为。
最基础的想法是:控制的goal 是long-term scalar cost function的优化问题。

构建一个最简单的二阶系统,
q
¨
=
u
,
∣
u
∣
≤
1
\ddot{q}=u, |u| \le 1
q¨?=u,∣u∣≤1
针对这个简单的二阶系统,一般步骤如下:
1)为每步设置policy,
π
(
x
,
t
)
\pi(x,t)
π(x,t)
2) 常见的optimal control formulation 如下:
2.1)时间最优
m
i
n
π
t
f
s
u
b
j
e
c
t
x
(
t
0
)
=
x
0
,
x
(
t
f
)
=
0
\begin{aligned} min_{\pi} & \quad t_f \\ subject & \quad x(t_0)=x_0, x(t_f)=0 \end{aligned}
minπ?subject?tf?x(t0?)=x0?,x(tf?)=0?
2.2)效率最优
m
i
n
π
∫
t
0
∞
[
x
(
t
)
T
Q
x
(
t
)
]
,
Q
>
0
min_{\pi} \quad \int_{t_0}^{\infin} [x(t)^TQx(t)], Q>0
minπ?∫t0?∞?[x(t)TQx(t)],Q>0
2.3) 限制输入
m
i
n
π
∫
t
0
∞
[
x
(
t
)
T
Q
x
(
t
)
+
u
T
R
u
]
,
Q
>
0
min_{\pi} \quad \int_{t_0}^{\infin} [x(t)^TQx(t)+u^TRu], Q>0
minπ?∫t0?∞?[x(t)TQx(t)+uTRu],Q>0
机器人系统中的pick-and-place的最优时间问题,控制系统中的LQR方法已经流行很长时间。随着计算机越来越强大,数值最优控制变得异常流行。现在开始构建滑块最短时间控制问题。
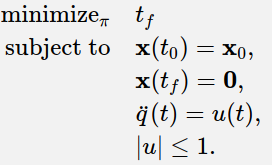
在学习数值方法找出最优策略前,人为的找出控制方法,直觉采用bangbang控制,能最快到达目标状态(先最大加速,到了某点一直减速,最终刚好停在了目标状态上)。
先看一下
u
=
?
1
u=-1
u=?1,减速时段的phase portrait 的轨道。
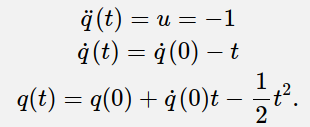
将公式中的t进行替换
t
=
q
˙
(
0
)
?
q
˙
t=\dot{q}(0)-\dot{q}
t=q˙?(0)?q˙?,得到
q
=
?
1
2
q
˙
2
+
c
?
,
c
?
=
q
(
0
)
+
1
2
q
˙
2
(
0
)
q=-\frac{1}{2}\dot{q}^2+c_{-}, \quad c_{-}=q(0)+\frac{1}{2}\dot{q}^2(0)
q=?21?q˙?2+c??,c??=q(0)+21?q˙?2(0)
绘制出phase portrait 如下图。

同样,再看
u
=
1
u=1
u=1,加速时段的phase portrait对应的轨道。
q
=
1
2
q
˙
2
+
c
+
,
c
+
=
q
(
0
)
?
1
2
q
2
(
0
)
q=\frac{1}{2}\dot{q}^2+c_{+}, \quad c_{+}=q(0)-\frac{1}{2}q^2(0)
q=21?q˙?2+c+?,c+?=q(0)?21?q2(0)
总结控制方法如下图,公式为:
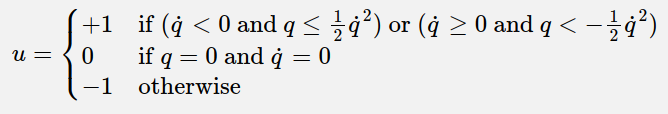
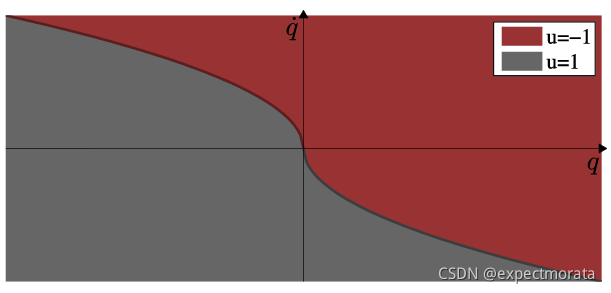
采用上面的控制策略,各种不同的初始状态的phase portrait如下图。

再计算一下,任意的初始状态到达零点的时间,以上图红色区域
u
=
?
1
u=-1
u=?1为例。
1)分析phase portrait的轨道变化:先沿着u=-1的轨道运动直到到了u=1的回归轨道,然后到达零点;
2)计算两个轨道的交点:
1
2
q
˙
t
2
=
?
1
2
q
˙
t
2
+
q
(
0
)
+
1
2
q
˙
2
(
0
)
q
˙
t
=
?
1
2
q
˙
2
(
0
)
+
q
(
0
)
\begin{aligned} \frac{1}{2}\dot{q}_t^2 &=-\frac{1}{2}\dot{q}_t^2+q(0)+\frac{1}{2}\dot{q}^2(0) \\ \dot{q}_t &= -\sqrt{\frac{1}{2}\dot{q}^2(0)+q(0)} \end{aligned}
21?q˙?t2?q˙?t??=?21?q˙?t2?+q(0)+21?q˙?2(0)=?21?q˙?2(0)+q(0)??
3 ) 计算总时间t,需要得到一个通用公式,
用
q
˙
表
示
q
˙
(
0
)
用\dot{q} 表示\dot{q}(0)
用q˙?表示q˙?(0):
t
=
q
˙
(
0
)
?
2
q
˙
t
=
q
˙
+
2
1
2
q
˙
2
+
q
\begin{aligned} t& = \dot{q}(0)-2\dot{q}_t \\ & = \dot{q}+2\sqrt{\frac{1}{2}\dot{q}^2+q} \end{aligned}
t?=q˙?(0)?2q˙?t?=q˙?+221?q˙?2+q??
4)总结公式和图像
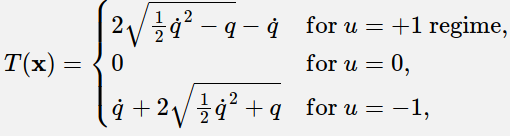

我们先通过直觉的方法找到了brick的控制策略,接下来看一下如何通过数值方法,搭建一套框架自动找出最优的控制策略。
7.1.1 additive cost
先定义一个抽象程序很高的一般性框架,用additive cost 构建目标函数,long-term 的得分如下:
∫
0
T
l
(
x
(
t
)
,
u
(
t
)
)
d
t
\int_0^T l(x(t),u(t))dt
∫0T?l(x(t),u(t))dt
其中,
l
(
)
l()
l()是瞬时的cost (running cost), 如果
T
=
∞
T=\infin
T=∞,则是一个infinite-horizon的问题。
接下来,就是通过构建数值优化的方法替代通过直觉的方法找到最优控制策略的过程,对于instantaneous cost,通常有两种方法:min_time_cost和quadratic_regulator_cost。
function cost = min_time_cost(x,u)
x(1) = x(1) - pi;
if dot(x, x) < .05
cost = 0.;
else
cost = 1.;
end
end
function cost = quadratic_regulator_cost(x,u)
x(1) = x(1) - pi;
cost = 2 * dot(x, x) + dot(u, u);
end
7.2 optimal control as graph search
dynamic programming 对于连续变量是围绕additive cost的最优控制问题;
dynamic programming 对于离散系统则是一系列带反馈控制器的数值解法。
对于一个典型的图搜索问题,可以用表示成下面的关系。
t
r
a
n
s
i
t
i
o
n
?
"
d
y
n
a
m
i
c
"
s
[
n
]
=
f
(
s
[
n
?
1
]
,
a
[
n
]
)
c
o
s
t
?
t
o
?
g
o
J
?
=
min
?
a
∈
A
[
l
(
s
i
,
a
i
)
+
J
?
(
s
i
,
a
i
)
]
p
o
l
i
c
y
P
i
(
s
i
)
=
arg?min
?
a
[
l
(
s
i
,
a
i
)
+
J
?
(
s
i
,
a
i
)
]
\begin{aligned} transition \, "dynamic" & \quad s[n] = f(s[n-1], a[n]) \\ cost \, to \, go & \quad J^* = \min \limits_{a\in A} [{l(s_i,a_i)}+J^*(s_i,a_i)] \\ policy & \quad Pi(s_i)=\argmin \limits_{a}[l(s_i,a_i)+J^*(s_i,a_i)] \end{aligned}
transition"dynamic"costtogopolicy?s[n]=f(s[n?1],a[n])J?=a∈Amin?[l(si?,ai?)+J?(si?,ai?)]Pi(si?)=aargmin?[l(si?,ai?)+J?(si?,ai?)]?
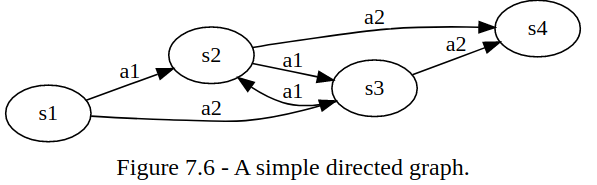
对于transition “dynamic”, 是由于action,引起的状态转换,可以用状态转移矩阵表示;
对于cost to go
for state = 1:num_state
for action = 1:nun_action
Q = instaneous_cost(state, action);
next_state = transition(state, action);
Q = Q + J(next_state);
end
end
对于policy,通过不停的迭代,直到所有状态的cost都达到了稳定状态。
max_diff = inf;
J = 0;
while max_diff < options
Jnext = cost_to_go();
max_diff = norm(J-Jnext, inf);
J = Jnext;
end
- example1: grid world
绘制cost function和phase portrait,phase portrait可以帮助进行debug,以及反映控制器是否合理。

- example2: double itegrator
在7.1部分,通过观察总结出了最优的控制策略,在这里通过值迭代的动态规划方法找到控制律。
对于连续系统,因为 s n + 1 = f ( s n , a n ) s_{n+1}=f(s_n,a_n) sn+1?=f(sn?,an?),得出的新状态不在离散状态点上,需要做权重插值。
绘制cost function和phase portrait, 通过dynamic programming得到的控制律和人为总结得出的控制律相同。
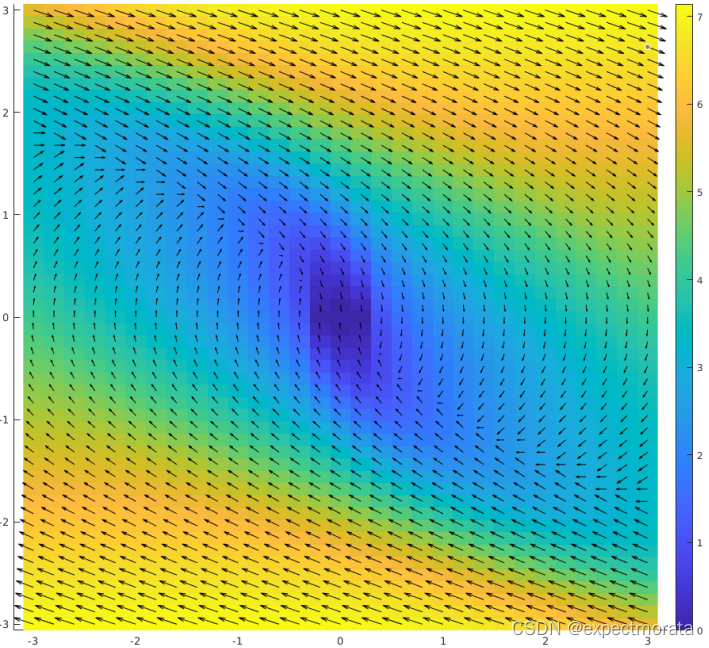
调试这类值迭代问题,关注三个问题
1)状态转移是否正确;
2)计算cost function是否正确,尤其是状态的权重插值是否正确;
3)观察max_diff的收敛速度;
7.3 Continuous dynamic programming
7.3.1 The Hamilton-Jacobi-Bellman Equation
推导过程抄至[1],公式推导的基础公式如下:
x
˙
(
t
)
=
f
(
x
(
t
)
,
u
(
t
)
)
x
(
t
)
=
x
(
0
)
+
∫
0
t
f
(
x
(
τ
)
,
u
(
τ
)
)
d
τ
J
(
x
0
,
u
)
=
∫
0
∞
g
(
x
(
t
)
,
u
(
t
)
)
d
t
u
(
t
,
x
0
)
=
arg?min
?
a
J
(
x
0
,
u
)
\begin{aligned} \dot{x}(t) & =f(x(t),u(t)) \\ x(t) &= x(0)+\int_0^t f(x(\tau),u(\tau))d\tau \\ J(x_0,u) &=\int_0^{\infin} g(x(t),u(t))dt \\ u(t, x0) & = \argmin \limits_{a} J(x_0,u) \end{aligned}
x˙(t)x(t)J(x0?,u)u(t,x0)?=f(x(t),u(t))=x(0)+∫0t?f(x(τ),u(τ))dτ=∫0∞?g(x(t),u(t))dt=aargmin?J(x0?,u)?
因为HJB公式中有差分项,用泰勒展开构建。
J
(
x
0
,
u
)
=
∫
0
Δ
t
g
(
x
(
t
)
,
u
(
t
)
)
d
t
+
∫
Δ
t
∞
g
(
x
(
t
)
,
u
(
t
)
)
d
t
≈
g
(
x
(
0
)
,
u
(
0
)
)
Δ
t
+
J
(
x
(
Δ
t
)
,
u
)
J
(
x
(
Δ
t
)
,
u
)
=
J
(
x
0
,
u
)
+
?
J
?
x
(
x
(
Δ
t
)
?
x
0
)
=
J
(
x
0
,
u
)
+
J
x
0
′
f
(
x
0
,
u
)
Δ
t
\begin{aligned} J(x_0,u) &=\int_0^{\Delta t} g(x(t),u(t))dt+\int_{\Delta t}^{\infin} g(x(t),u(t))dt \\ & \approx g(x(0),u(0)) \Delta t+J(x(\Delta t), u) \\ J(x(\Delta t), u) & = J(x_0, u)+ \frac{\partial J}{\partial x}(x(\Delta t)-x_0) \\ & = J(x_0, u)+J'_{x0}f(x_0,u)\Delta t \end{aligned}
J(x0?,u)J(x(Δt),u)?=∫0Δt?g(x(t),u(t))dt+∫Δt∞?g(x(t),u(t))dt≈g(x(0),u(0))Δt+J(x(Δt),u)=J(x0?,u)+?x?J?(x(Δt)?x0?)=J(x0?,u)+Jx0′?f(x0?,u)Δt?
得到化简后的公式为:
g
(
x
(
0
)
,
u
(
0
)
)
+
J
x
?
(
x
0
)
f
(
x
0
,
u
)
=
0
g(x(0),u(0)) + J^*_{x}(x_0)f(x_0,u)=0
g(x(0),u(0))+Jx??(x0?)f(x0?,u)=0
目
前
对
H
J
B
公
式
的
理
解
不
太
深
,
尤
其
J
x
?
(
x
0
)
的
理
解
。
\color{red}{目前对HJB公式的理解不太深,尤其J^*_x(x_0)的理解。}
目前对HJB公式的理解不太深,尤其Jx??(x0?)的理解。
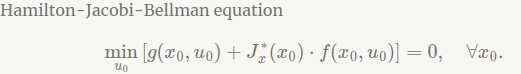
References
- http://boris-belousov.net/2017/11/23/hjb/