转眼又是打卡的截点,只好金戈铁甲,重新上阵。
首先,无论是前面的线性模型还是这一章的决策树,都是希望从给定数据集中学得一个模型可以用来对新样本做出预测,也就是说,都是一种机器学习方法。
那决策树是什么?有什么特点呢?怎么工作的呢?这种方法会遇到什么问题呢?
回想一下前面的线性模型有什么特点?
嗯,线性模型的特点在于通过它本质上是一种线性变换的函数(广义的线性模型也是在这个线性变换wx+b的基础上进行一层非线性的)
ok,什么是决策树?一种机器学习方法,一种对已有数据集建立决策模型的算法,一种结构为树形的算法。
then,如何决策?决策的关键点在于什么?
首先搞清楚三个关键的数据:数据集中样本数D,数据的数据集中的属性类别,属性值(连续or离散)。
以及决策的目标(无论做什么算法,都是奔着某种目的功能去的):决策树的分支结点所包含的样本尽可能属于同一类别。也即结点的纯度越来越高。
那如何定量地衡量纯度这一概念呢?ok,信息熵来了。
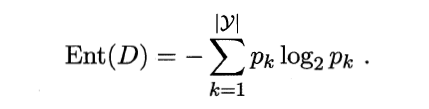
Pk指类别k的样本占总样本的比例。Pk越大,Ent(D)的值越小,D的纯度越高。(看公式左边的变量,D,可以知道信息熵的主语是D,也就是一群样本才有信息熵!)
那划分的时候应该选择哪个属性作为划分依据呢?
ok,对于某个属性a,它应该有很多不同的可能的取值,把可能的取值(a1,a2…aV)个数记为V。
那如果用这个属性来对数据集D进行划分,就会产生V个分支结点,其中属性值为av的样本为Dv。无论是D还是Dv(都是一群样本),都可以计算它们的信息熵。
你看,当我们利用这个属性a来划分之后,会得到V个分支结点,每个节点有一小群样本Dv,Dv有它的信息熵,自然而然地,我们会想到用∑Ent(Dv)来代表这个属性划分的好坏,因为所有结点的信息熵之和最小不就最好吗?
确实是这样,但还要考虑一下不同结点它样本大小不一样,在最后的信息熵总和中占的权重也应该有所不同,按照这种朴素的想法,就可以得到一个新的名词——信息增益:
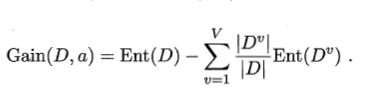
同样地,注意看等式左边括号里的变量,就可以知道信息增益的主人是谁了,没错,样本集D用属性a进行划分的信息增益。
显然,等式右边减号后面的式子的值越小,就代表属性a的划分结果越好,也就是说G越大,属性a的划分越如意。
ok,讲了这么多,只解决了一件事。
可以通过定量求解每个属性a的信息增益来决定选取哪一个属性进行划分。
但这个思路可是一劳永逸哦。你想想,决策树,它不就是一直分叉吗,选哪个属性来开叉已经胸有成竹了,不就可以完成这颗决策树的构造吗。
下面考虑更细致的一些算法准则:
比如说,信息增益准则对于可取值较多的属性有天然的侧重,也就是说有点不公平,为了更加公平,C4.5决策树算法使用“增益率”来进行属性选取。
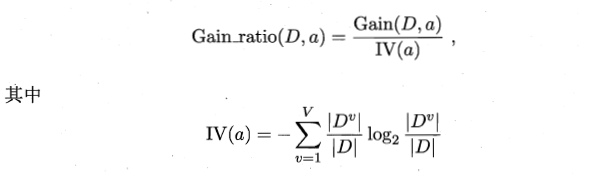
其中IV是属性a的固有值,可以抵消一点因为某种属性取值较多而造成的影响。
基尼指数:
