?每一种算法都带有一种归纳偏好,归纳偏好,可以理解为算法对于某种假设的偏好,这种偏好可以体现为线性回归模型对于模型线性的假设偏好等。
奥卡姆剃刀原理
关于归纳偏好,对于一个数据,模型有许多的归纳偏好,也就是有许多的假设,那么如何进行归纳假设的选择呢,一般性的原则就是:最简单原则-奥卡姆剃刀原理,也就是使模型的结构尽量简单,这也是《统计学习》中提到的结构风险最小化。
简单有什么好处呢,其中之一就是具有良好的泛化性,如果结构过于复杂,会产生过拟合的现象。
NFL(没有免费的午餐)
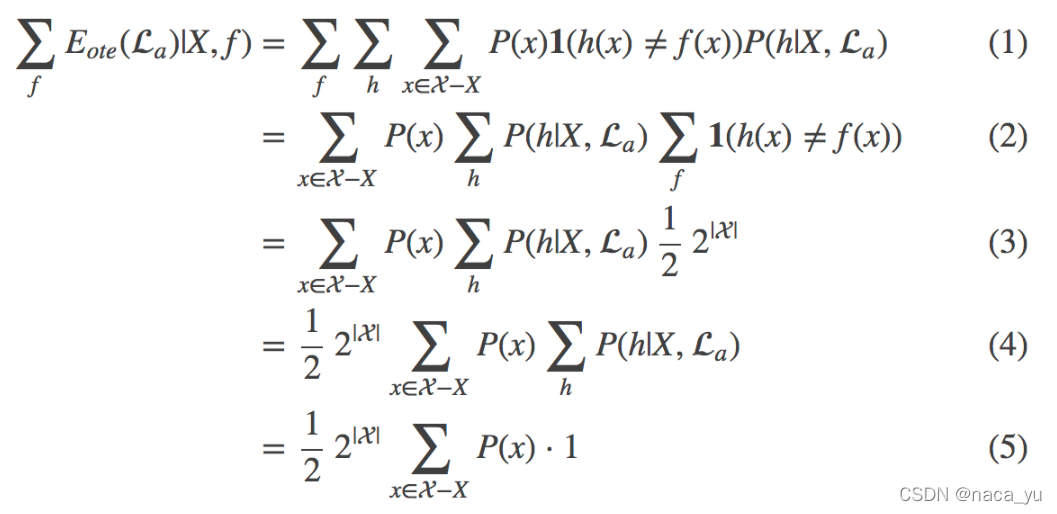
如图,见详情可见机器学习p9,这个式子作以下说明:
- 假设:P(f i)几率相等,也就是说每个目标函数的概率相等(f 就是各类问题所对应的目标函数,而La就是带有归纳偏好的选择算法)
- 公式解释:E代表使用La算法(某种归纳偏好),对所有的问题求解所产生的总误差(注意,是对所有问题)
- 公式的证明目的:证明使用某种算法(带有某种归纳偏好)求解所有问题,所产生的误差只与数据本身有关,与学习算法无关,这里也就是说:如果你想用一种招式打遍天下,输赢的局数,和你的招式是无关的,也就是 “天下没有免费的午餐”。
?这里周教授并不是说选择什么算法都没有用了,我们不要忽略这样的前提:所有问题出现的概率相等,举个例子:两种瓜让我们分辨是否是好瓜,一种是带有特征A, 一种是特征B,我们有两种推理规则f1(判断A类型为好瓜,B为坏瓜), f2(判断原则相反),那么如果假设两种瓜出现的概率相等(问题出现的几率相等),那么我们应用f1或者f2 去判断两种问题 都是相同的误差,此时算法就失效了,但是,A特征的瓜世界有200个,但是B特征的瓜有1个,那么我们针对A类型的瓜挑取,当然选择f1作为依据,而不是整体考虑所有类型的瓜。
总结
?这就要告诉我们:算法本身就是一种归纳偏好,如果所有的问题出现概率相等,那么解决所有问题产生的总误差,与你选择的算法无关,某个算法只在某个问题上才有意义。我们要具体问题,具体分析!