[人工智能]基于Pytorch对凸函数采用SGD算法优化实例（附源码）

实例说明

基于Pytorch，手动编写SGD（随机梯度下降）方法，求-sin²(x)-sin²(y)的最小值，x∈[-2.5 , 2.5] , y∈[-2.5 , 2.5]。

画一下要拟合的函数图像

代码

import matplotlib.pyplot
from mpl_toolkits.mplot3d import Axes3D
import numpy
import os  #这句要加，要不画图会报错
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE' #这句要加，要不画图会报错

def fix_fun(x,y):  #构建函数fix_fun = (x^2+y+10)^4+(x+y^2-5)^4
    return -numpy.sin(x)**2 - numpy.sin(y)**2

#画一下函数图像
x = numpy.arange(-2.5,2.5,0.1)
y = numpy.arange(-2.5,2.5,0.1)
x, y = numpy.meshgrid(x, y)
z = fix_fun(x,y)
fig = matplotlib.pyplot.figure()
ax = Axes3D(fig)
ax.plot_surface(x,y,z, cmap='rainbow')
matplotlib.pyplot.show()

画出来后，曲面长下面的样子↓

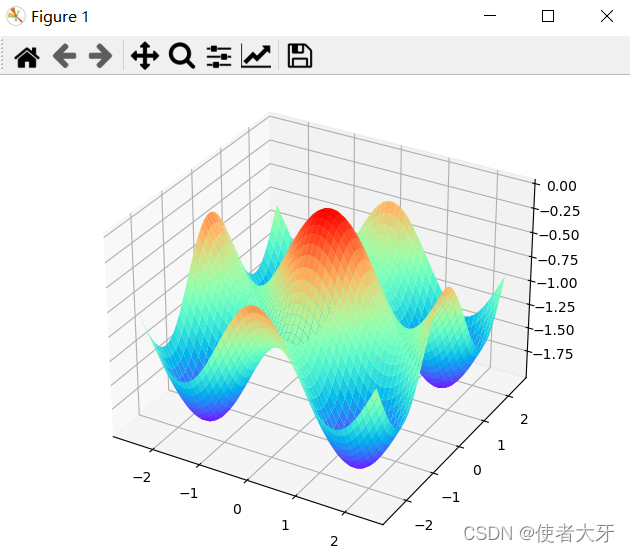
SGD算法构建思路

非常简单：用.backward()方法求出要优化的函数的梯度，按照SGD的定义找出最优解。
即：
θ=θ-η·▽J(θ)

运行结果

看看随机生成的几个优化的结果

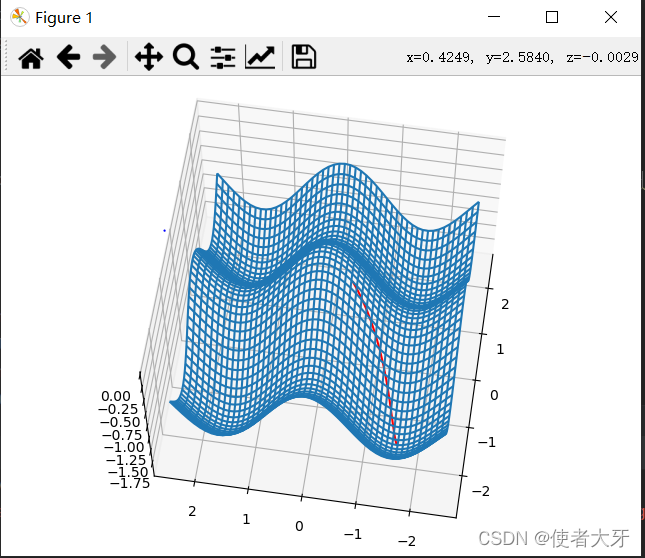
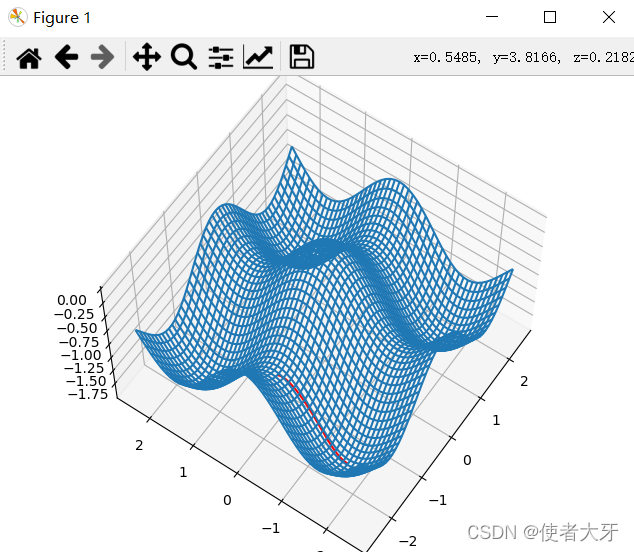
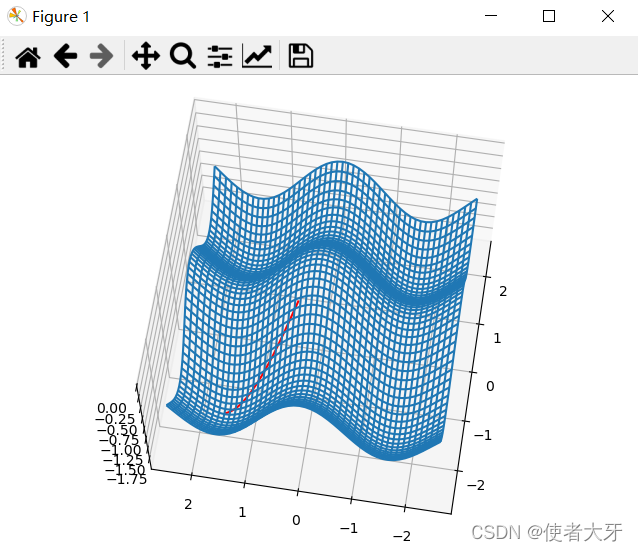
源码

老规矩，细节的备注仍然写在代码里面。

import torch
from torch.autograd import Variable
import matplotlib.pyplot
from mpl_toolkits.mplot3d import Axes3D
import numpy
import os  #这句要加，要不画图会报错
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE' #这句要加，要不画图会报错

def fix_fun_numpy(x,y):  #构建函数fix_fun（因为tensor数据类型和numpy画图不能混用，构建两个函数）
    return -numpy.sin(x)**2 - numpy.sin(y)**2
def fix_fun_tensor(x,y):  #构建函数fix_fun
    return -torch.sin(x)**2 - torch.sin(y)**2

#画一下函数图像
x = numpy.arange(-2.5,2.5,0.1)
y = numpy.arange(-2.5,2.5,0.1)
x, y = numpy.meshgrid(x, y)
z = fix_fun_numpy(x,y)
fig = matplotlib.pyplot.figure()
ax = Axes3D(fig)



#构建SGD算法
X = (torch.rand(2,dtype=float)-0.5)*5 #0~1分布改成-2.5~2.5分布，生成随机初始点（所以叫‘随机’梯度下降）
X_dots = []
Y_dots = []
Z_dots = []

for iter in range(50):
    X = Variable(X, requires_grad = True)  #需要求导的时候要加这一句
    Z = fix_fun_tensor(X[0],X[1])  #这一句一定要写在Variable后面
    Z.backward()  #求导（梯度）
    X = X - 0.1*X.grad #learning rate=0.1
    X_dots.append(X[0].detach().numpy())  #记录下每个学习过程点（为了后面画出学习的路径）
    Y_dots.append(X[1].detach().numpy())
    Z_dots.append(Z.detach().numpy())

ax.plot_wireframe(x, y, z)  #换成wireframe，因为用surface会和曲线重合，看不出来
ax.plot(X_dots,Y_dots,Z_dots,color='red')

matplotlib.pyplot.show()

后记

喜欢探索的同学还可以把上面的源码改一改，并试试Adagrad, Adam, Momentum这些方法，也对比下各自的优劣。