哈喽,大家好。
之前写了几篇 Python 基础的文章,效果不错。为感谢大家的支持,月底搞一波抽奖送书活动。
闲话少叙,今天来详解一个 Python 库 ——?NumPy。
NumPy是 Python 科学计算的基本包,几乎所有用 Python 工作的科学家都利用了NumPy的强大功能。此外,它也广泛应用在开源的项目中,如:Pandas、Seaborn、Matplotlib、scikit-learn等。

Numpy应用的领域
举个栗子,直观感下NumPy的强大。
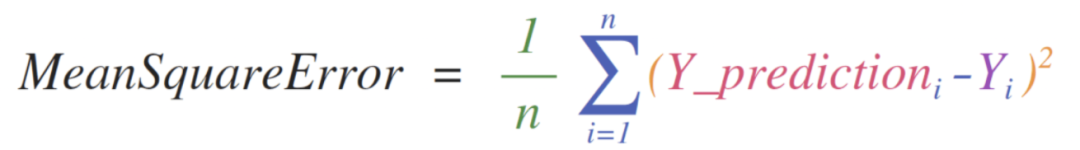
均方差公式
上图是计算均方差的公式,其中Y_prediction和Y是数组。
下面是用NumPy代码,一行便可完成。

NumPy计算均方差
NumPy结合可视化库,可以用几行代码,绘制出下面的数学函数图
记得学高中学数学的时候,画函数图都要自己在本上描点,而现在用NumPy,几行代码就搞定,既快又准确。
简单认识NumPy后,下面进入详解
1. 与list的区别
NumPy和list都是数组结构,那它们之间有什么区别呢?
-
NumPy数组中所有元素的数据类型是相同的。 -
NumPy底层经过充分优化的 C 语言代码,计算性能比list高。 -
NumPy提供了全面的数学函数可以直接应用在NumPy数组上。
2. 创建数组
NumPy中定义的数组叫ndarray,n-dimensions-array 即:n维数组。
用np.array()函数可以创建NumPy数组
>>>?import?numpy?as?np
>>>?a?=?np.array([1,?2,?3])?#创建ndarray数组
>>>?a
array([1,?2,?3])
>>>?type(a)
<class?'numpy.ndarray'>
a就是NumPy数组,也是numpy.ndarray类对象,该类定义了几个常用的属性
-
ndarray.ndim:维度的数量,二位数组ndim是 2 -
ndarray.shape:元组,每位代表该维度上元素个数,元组长度等于ndim -
ndarray.size:数组中元素总数 -
ndarray.dtype:数组中元素的数据类型 -
ndarray.itemsize:数组中元素存储大小(以字节为单位)
>>>?a?=?np.array([[1,2,3],?[4,5,6]])
>>>?a
array([[1,?2,?3],
???????[4,?5,?6]])
>>>?a.ndim
2
>>>?a.shape
(2,?3)
>>>?a.size
6
>>>?a.dtype
dtype('int64')
>>>?a.itemsize
8
除了np.array()创建数组外,还有下面的方式创建数组
>>>?np.zeros((2,3))?#?以0填充的二维数组
array([[0.,?0.,?0.],
???????[0.,?0.,?0.]])
>>>?np.ones((2,3))?#?以1填充的二维数组
array([[1.,?1.,?1.],
???????[1.,?1.,?1.]])
>>>?np.empty((2,3))?#?空的二维数组,内容为当时内存中的值
array([[1.,?1.,?1.],
???????[1.,?1.,?1.]])
>>>?np.arange(6)?#?用法跟range函数一样
array([0,?1,?2,?3,?4,?5])
>>>?np.linspace(0,?10,?num=5)?#?以指定的线性间隔为初值,创建数组
array([?0.?,??2.5,??5.?,??7.5,?10.?])
>>>?rng?=?np.random.default_rng(0)?#?以随机数创建二维数组
>>>?rng.random((2,3))
array([[0.63696169,?0.26978671,?0.04097352],
???????[0.01652764,?0.81327024,?0.91275558]])
3. 访问数组
支持索引和切片。格式为:
arr[i, j, k, ...],i, j, k分别代表数组第0维、第1维、第2维
其中,i, j, k的格式为:
s1:s2:s3,分别代表开始下标,结束下标和步长
步长s3不填时,第二个冒号可省略,步长为1。
以一个3维数组为例
>>>?#?创建?5*4?二维数组(5行4列)
>>>?c?=?np.array([[?0,??1,??2,??3],?[10,?11,?12,?13],?[20,?21,?22,?23],?[30,?31,?32,?33],?[40,?41,?42,?43]])
>>>?c
array([[?0,??1,??2,??3],
???????[10,?11,?12,?13],
???????[20,?21,?22,?23],
???????[30,?31,?32,?33],
???????[40,?41,?42,?43]])
>>>?c.shape
(5,?4)
>>>?#?按照索引取?第1行,第2列的元素
>>>?c[1,?2]
12
>>>?#?切片,取?1~2?行,第2列的元素(数组)
>>>?c[1:3,?2]
array([12,?22])
>>>?#?切片,取?1~2?行,第2~3列元素(数组)
>>>?c[1:3,?2:4]
array([[12,?13],
???????[22,?23]])
>>>?#?步长=2,取到第?1,?3?行,第2~3列元素
>>>?c[1:6:2,?2:4]
array([[12,?13],
???????[32,?33]])
如果取最后一维,下标为2的元素,可以按照下面方式取
>>>?c[:,2]
array([?2,?12,?22,?32,?42])
如果维度比较多,需要写很多:,NumPy提供...可以代表之前或之后的任意维度
>>>?c[...,2]
array([?2,?12,?22,?32,?42])
取第0维的写法也是一样的。
4. 运算(四则运算和函数)
NumPy数组支持四则运算,它会将两个数组相同位置的数值进行加减乘除,生成新的数组。
>>>?data?=?np.array([1,?2])
>>>?ones?=?np.ones(2,?dtype=int)
>>>?data?+?ones
array([2,?3])
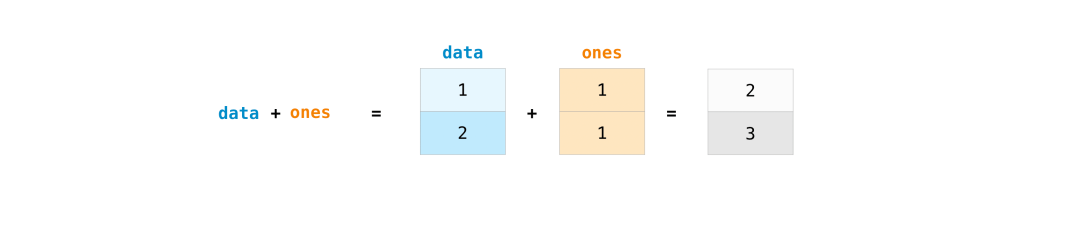
NumPy数组相加
除了基本的四则运算符,还支持+=、-=、*=和/=增量赋值运算符,可修改原数组的值。
除了运算符NumPy中还提供了一些函数用于快速计算数组中的值。如sum、min、max和mean等。
>>>?a?=?np.array([[1,2,3],[4,5,6]])
>>>?np.sum(a)
21
上面例子中np.sum()函数对二维数组中所有元素求和。
这类函数不光可以对所有元素做计算,还支持按照指定维度计算。如:
>>>?#?按照第0维相加(行相加)
>>>?a.sum(axis=0)
array([5,?7,?9])
>>>?#?按照第1维相加(列相加)
>>>?a.sum(axis=1)
array([?6,?15])
参数axis指定对第几维做计算,在NumPy经常会用到这个参数。
很多教程,包括官网文档,直接告诉读者axis=0代表按行计算,axis=1代表按列计算。
我觉得这样说有局限性,一来容易记混,二来如果是三维或者更高维谁是行,谁又是列呢。
所以,我觉得干脆不要记行、列,只要记住axis的取值就是第几维就好了。
比如,在三维数组的各维度运用np.sum()
>>>?a?=?np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
>>>?a
array([[[?1,??2,??3],
????????[?4,??5,??6]],
???????[[?7,??8,??9],
????????[10,?11,?12]]])
>>>?a.shape
(2,?2,?3)
按第0维相加
>>>?a.sum(axis=0)
array([[?8,?10,?12],
???????[14,?16,?18]])
第0维里面有两个元素,每个元素都是二维数组,按照第0维相加就是将这俩二维数组相加,即:[[ 1, 2, 3],[ 4, 5, 6]] + [ 7, 8, 9],[10, 11, 12]]。上面说了,NumPy数组相加,相同位置的数值直接相加即可,得到就是上面的结果。
按第1维相加
>>>?a.sum(axis=1)
array([[?5,??7,??9],
???????[17,?19,?21]])
第1维共有4个一维数组,但由于处在两个第0维元素中,所以要分别计算,即:[ 1, 2, 3] + [ 4, 5, 6]?和?[ 7, 8, 9] + [10, 11, 12],最终返回两个一维数组。
按第2维相加
>>>?a.sum(axis=2)
array([[?6,?15],
???????[24,?33]])
第2维是最内层的数字,直接将数字相加即可。得到 4 个数字。
按照这种方式去推导每一维的计算逻辑才是最容易理解的,而不是教条的去记是行或者列。
5. 广播
上面的运算中,运算符两边的数组都是相同维度的。
而实际中,可能会有不同维度的数组相加减,这时候NumPy会自动将两边的数组维度调整相同后,再做计算,这个过程就叫广播。
>>>?data?=?np.array([1.0,?2.0])
>>>?data?*?1.6
array([1.6,?3.2])
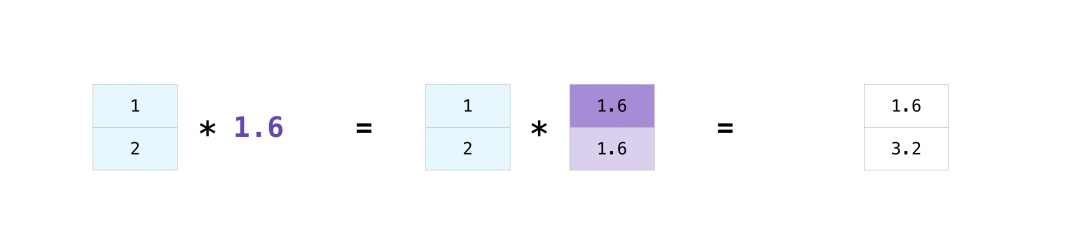
在此,NumPy将数字1.6广播成与data维度相同的一维数组,并用1.6填充,这样就变成了两个一维数组相乘。
当然,并不是任何情况都能广播成功,规则是:从两个数组最右侧维度开始,依次向左判断是否满足以下两个条件:
-
它们是相等的
-
其中一个为1
满足一个条件即可,如果都不满足,则抛ValueError: operands could not be broadcast together错误。
举个栗子:
A??????(4维数组):??8?x?1?x?6?x?1
B??????(3维数组):??????7?x?1?x?5
广播后??(4维数组):??8?x?7?x?6?x?5
从右往左,要么A维度是1,要么B维度是1,满足规则,可以广播。
如果改成
A??????(4维数组):??8?x?1?x?6?x?2
B??????(3维数组):??????7?x?1?x?5
就会报错,最右边两个维度,既不相等,也不是1。
再看一个计算的例子:
x?=?np.array([[1],[2],[3],[4]])
y?=?np.array([1,2,3,4])
>>>?x?+?y
array([[2,?3,?4,?5],
???????[3,?4,?5,?6],
???????[4,?5,?6,?7],
???????[5,?6,?7,?8]])
x会被广播成4*4的数组
[[1,?1,?1,?1],
?[2,?2,?2,?2],
?[3,?3,?3,?4],
?[4,?4,?4,?4]]
y也会被广播成4*4的数组
[[1,?2,?3,?4],
?[1,?2,?3,?4],
?[1,?2,?3,?4],
?[1,?2,?3,?4]]
二者按照数组规则直接相加即可。
6. 重塑数组
NumPy提供了很多函数可以更改数组的形状(维度)。
reshape函数
>>>?a?=?np.arange(10)
>>>?a.reshape(5,2)
array([[0,?1],
???????[2,?3],
???????[4,?5],
???????[6,?7],
???????[8,?9]])
reshape()函数可以修改数组的维度,本例中将一个一维数组修改成5行2列的二维数组。
transpose函数
>>>?a?=?np.array([[1,2],[3,4],?[5,6]])
>>>?a.transpose()
array([[1,?3,?5],
???????[2,?4,?6]])
transpose()函数可以转置数组,实现线性代数里矩阵转置的效果。
![]()
数组转置
该函数也可以用a.T来代替。
反转数组
np.flip()函数可以反转数组。
>>>?a?=?np.array([[1,?2,?3,?4],?[5,?6,?7,?8],?[9,?10,?11,?12]])
>>>?a
array([[?1,??2,??3,??4],
???????[?5,??6,??7,??8],
???????[?9,?10,?11,?12]])
>>>?np.flip(a)
array([[12,?11,?10,??9],
???????[?8,??7,??6,??5],
???????[?4,??3,??2,??1]])
np.flip函数默认将所有元素从左至右、从上至下全部反转。当然,也可以按照某维反转
>>>?#?按行反转
>>>?np.flip(a,?axis=0)
array([[?9,?10,?11,?12],
???????[?5,??6,??7,??8],
???????[?1,??2,??3,??4]])
>>>?#?按列反转
>>>?np.flip(a,?axis=1)
array([[?4,??3,??2,??1],
???????[?8,??7,??6,??5],
???????[12,?11,?10,??9]])
扁平化数组
flatten()和ravel()函数可以将多维数组拉平成一维数组,区别在于前者会返回新的数组,而后者只是创建了原数组的视图。
>>>?a?=?np.array([[1?,?2,?3,?4],?[5,?6,?7,?8]])
>>>?a
array([[1,?2,?3,?4],
???????[5,?6,?7,?8]])?
>>>?b?=?a.flatten()
>>>?b
array([1,?2,?3,?4,?5,?6,?7,?8])
>>>?b[0]?=?10
>>>?b
array([10,??2,??3,??4,??5,??6,??7,??8])
>>>?a
array([[1,?2,?3,?4],
???????[5,?6,?7,?8]])
a是二维数组,经过flatten函数拉平后变成一维数组b,修改b数组的值,不会影响数组a。
>>>?a?=?np.array([[1?,?2,?3,?4],?[5,?6,?7,?8]])
>>>?b?=?a.ravel()
>>>?b
array([1,?2,?3,?4,?5,?6,?7,?8])
>>>?b[0]?=?10
>>>?a
array([[10,??2,??3,??4],
???????[?5,??6,??7,??8]])
数组a经过ravel函数拉平成一维数组b,修改b中值会影响数组a。
这里会发现一个现象,数组a的仍然是二维数组,说明raval只是建立了a的视图,并没有改变a本身的存储结构。
如果想修改b而不影响a,可以调用copy()函数
>>>?c?=?b.copy()
>>>?c
array([10,??2,??3,??4,??5,??6,??7,??8])
>>>?c[0]=100
>>>?a
array([[10,??2,??3,??4],
???????[?5,??6,??7,??8]])
copy()函数会创建一个新数组,并用原数组的值填充,因此修改新数组不会影响原数组。这个过程也叫做深拷贝。
重塑数组的函数还有很多,如:
-
np.sort():排序 -
np.hstack():横向合并数组 -
np.vstack():纵向和并数组 -
np.concatenate():按维合并数组
等等等等。
用法上并不复杂,大家可以参考官方文档学习一下。
7. 高级访问
7.1 索引数组
第3小节讲解访问数组时,都是通过数字来访问。NumPy支持按照数组格式访问数组。
>>>?a?=?np.arange(12)
>>>?i?=?np.array([1,?1,?3,?8,?5])
>>>?a[i]?
array([1,?1,?3,?8,?5])
数组i是一个索引数组,它里面的值都可以当做a的下标来访问。
也可以通过同样的方式访问多维数组。
>>>?a?=?np.array([[0,?0,?0],?[255,?0,?0],?[0,?255,?0],?[0,?0,?255],?[255,?255,?255]])
>>>?a
array([[??0,???0,???0],
???????[255,???0,???0],
???????[??0,?255,???0],
???????[??0,???0,?255],
???????[255,?255,?255]])
>>>?i?=?np.array([[0,?1,?2,?0],?[0,?3,?4,?0]])
>>>?a[i]
array([[[??0,???0,???0],
????????[255,???0,???0],
????????[??0,?255,???0],
????????[??0,???0,???0]],
???????[[??0,???0,???0],
????????[??0,???0,?255],
????????[255,?255,?255],
????????[??0,???0,???0]]])
访问多维数组,索引数组i中的数值,都将作为数组a中的第0维的下标。
当然索引数组并非只能访问第0维,也能支持多个索引数组访问同一个数组多个维度。
>>>?a?=?np.arange(12).reshape(3,?4)
>>>?a
array([[?0,??1,??2,??3],
???????[?4,??5,??6,??7],
???????[?8,??9,?10,?11]])
>>>?i?=?np.array([[0,?1],?[1,?2]])
>>>?j?=?np.array([[2,?1],?[3,?3]])
>>>?a[i,?j]
array([[?2,??5],
???????[?7,?11]])
索引数组的维度必须相同,排在第一位的索引数组i访问第0维,排在第二位的索引数组j访问第1维,以此类推。i和j相同位置的数字正好对应数组a中的某行某列的元素。
7.2 布尔数组
索引数组可以是个布尔类型的数组,True代表保留元素,False代表删除元素。
>>>?a?=?np.arange(12).reshape(3,?4)
>>>?b?=?a?>?4
>>>?a[b]
array([?5,??6,??7,??8,??9,?10,?11])
>>>?a[a?>?4]
array([?5,??6,??7,??8,??9,?10,?11])
因为a和b形状一样,所以返回的结果是一维数组。?
当然也可以指定维度来筛选 滋补小铺?www.zibuxiaopu.com
>>>?a?=?np.arange(12).reshape(3,?4)
>>>?b1?=?np.array([False,?True,?True])
>>>?b2?=?np.array([True,?False,?True,?False])
>>>?a[b1,?:]
array([[?4,??5,??6,??7],
???????[?8,??9,?10,?11]])
>>>?a[:,?b2]
array([[?0,??2],
???????[?4,??6],
???????[?8,?10]])
>>>?a[b1,?b2]
array([?4,?10])
到这里,我们就把NumPy结构、访问和操作都讲解完了,涵盖了NumPy大部分常用的功能。
有了这篇详解,相信大家不管是直接用还是再看官方文档都会很容易。
如果本文对你有用就点个?在看?鼓励一下吧。