目录
一、Moravec算子介绍
1.基本原理
这是一种基于灰度方差的角点检测算子,该算子计算图像中每个像素点沿着水平、垂直、对角线及反对角线的四个方向的灰度方差,其中的最小值选作该像素点的兴趣值 IV,再通过局部非极大值抑制来检测其是否为特征点(角点)。
2.算法步骤
(1)计算各像元的兴趣值IV(Interest Value) 。以像素*(c,r)* 为中心的 w x w的影像窗口(如 5x5 的窗口),计算下图中所示四个方向相邻像素灰度差的平方和:
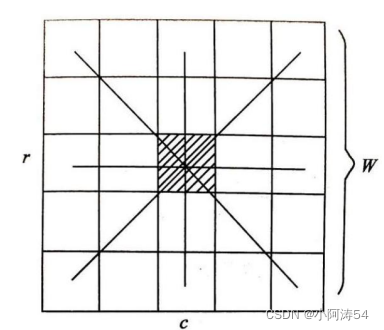
其计算公式为:
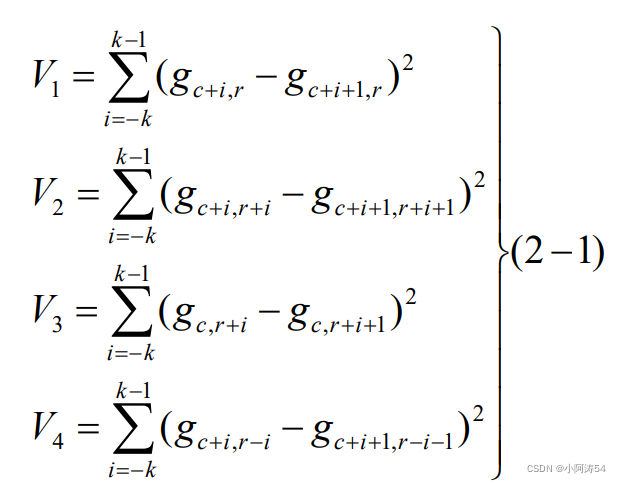
其中k =INT (w/ 2),即窗口的一半取整。取其中最小者作为该像素(c,r)的兴趣值。
(2)给定一经验阈值,将兴趣值大于该阈值的点作为候选点。阈值的原则应以候选点中包括的所需要的特征点而又不含过多的非特征点为原则。
(3)选取候选点中的极值点作为特征点。在一定大小的窗口内,将候选点中兴趣值不是最大者均去掉,仅留下一个兴趣值最大者,该像素即为一个特征点(抑制局部非最大)。
二、基于C语言的算法描述
1.影像数据介绍
已知同一地点的左右两张 bmp 格式的影像,其中左影像的大小为 1023x942px,右影像的大小为 805x887 px,如下图所示:

2.编程思路
- 使用 OpenCV 以灰度图的方式读取目标影像(左);
- 定义一个指定大小的兴趣值窗口wxw,其一半大小为k = int(w/ 2);
- 定义与目标图像相同大小的单通道兴趣值矩阵valueMat ,用来存储每个像素的兴趣值(外围像素由于无法计算则默认为 0);
- 以图像左上角为原点,从图像的第(k, k) 个元素开始,滑动此窗口,同时计算每个窗口中心像素四个方向相邻像素的灰度差平方和,并选取最小值作为中心像素的兴趣值,接着将其存入valueMat ,这样就把兴趣值及其坐标关联起来;
- 定义一个抑制窗口m x m ,其一半大小为n = int(m / 2) ;
- 定从valueMat 矩阵的第(n, n) 像素开始,以其为中心滑动抑制窗口,选出窗口内兴趣值最大的像素点,若其兴趣值大于给定阈值,则其作为特征点。为了避免特征点的重叠,该抑制窗口的大小可以设置得稍大一些。这样就得到了特征点的坐标(x, y),将其存入 vector 数组;
- 以 RGB 方式重新读取目标影像(为了标记效果明显),遍历 vector 特征点数组,将其标记在新的目标影像中即得到目标影像特征点提取结果。
3.特征点提取算法阈值设定分析
- 首先,统计每个抑制窗口内最大兴趣值,并进行可视化:
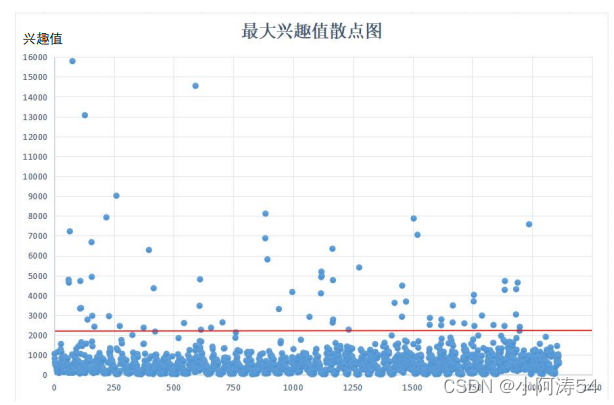
- 进一步,对其进行细化得到如下图:
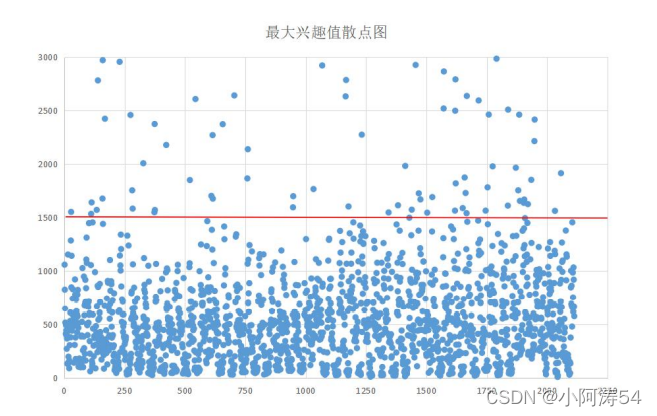
设置兴趣值窗口为7,已知窗口为21,调节阈值得到如下结果: - 阈值threshold=1000:

- 阈值threshold=1500,2000:

结论:最后分析以上三图,可知当阈值为 1000 时的非明显特征点较多,因此应当提高阈值,结合散点图,阈值应该大于 1500,当阈值等于 1500 时,图像仍存在一些非特征点;当阈值提到到 2000 时,虽然非明显特征点被舍去,但是一些明显特征点也被舍去(如图九,图十中红圈所示),因此阈值应该介于 1500-2000。最终结合视觉效果,阈值选为 1700:

4.窗口大小对特征点提取结果的影响
1.兴趣值窗口:
- 兴趣值窗口直接影响 Moravec 算子提取的特征点的个数,兴趣值窗口直接影响 Moravec 算子提取的特征点的个数:
| 兴趣值窗口 | 特征点个数 |
|---|---|
| 5*5 | 62 |
| 7*7 | 88 |
| 9*9 | 133 |
2.抑制窗口:
- 影响特征点的密度,密度越低,特征点的个数越少。
三、代码实现
1.OpenCV的配置
- OpenCV的配置见文章:VS2015OpenCV的配置.
- 提取码:howo
2.C语言代码
#include"stdafx.h"
#include<stdlib.h>
#include <opencv2/core.hpp>
#include <opencv2/imgcodecs.hpp>
#include<opencv2/highgui/highgui.hpp>
#include<opencv2/imgproc/imgproc.hpp>
#include<iostream>
#include<Windows.h>
#include<time.h>
using namespace std;
using namespace cv;
//以左影像为主影像进行特征点提取
//莫拉维克函数(参数:影像,兴趣值窗口,经验阈值,抑制窗口,特征点数组)
Mat Moravec(Mat srcImg, int winSize, int threshold, int restrainWinSize, vector <Point3f> &featurePt);
int main()
{
//打开目标影像(左)。PS:图片放在相同目录中
string image_path= "u0369_panLeft.bmp";
//读入灰度图像
Mat img_source = imread(image_path, IMREAD_GRAYSCALE);
//如果为空的话提示打不开
if (img_source.empty())
{
cout<<"Could not read the imageL"<<endl;
system("pause");
return 1;
}
//定义特征点提取的窗口大小(可以自己尝试改变窗口大小观察对结果的影像)
int winSize = 9;
//定义数组,存储特征点坐标(x,y)
vector <Point3f> featurePt1;//存储特征点的数组
//进行随机特征点的提取。设置原图像,窗口,阈值以及抑制窗口大小
cout<<"正在进行影像特征点随机提取...."<<endl;
//计时
clock_t start1 = clock();
//featureImg是提取后得到的影像
Mat featureImg = Moravec(img_source, winSize, 1700,21,featurePt1);
clock_t finish1 = clock();
cout << "耗时:" << (double)(finish1 - start1) / CLOCKS_PER_SEC << "s" << endl;
//保存特征点图像
imshow("特征点提取影像(左)", featureImg);
waitKey(0);
//另存为
imwrite("featureImg1.jpg", featureImg);
cout << "保存到当前文件目录中" << "featureImg1.jpg" << endl;
return 0;
}
//莫拉维克特征提取函数
Mat Moravec(Mat srcImg, int winSize, int threshold, int restrainWinSize,vector <Point3f> &featurePt)
{
//得到图像大小
int rows = srcImg.rows; //y,注意行row代表y值
int cols = srcImg.cols; //x,注意列col代表x值
//得到特征窗口的一半,记得去int
int k = winSize / 2;
//用来存储像素兴趣值的矩阵
Mat valueMat = Mat::zeros(srcImg.rows, srcImg.cols, CV_32FC1);
//循环,对每个像元(c,r)计算其四个方向的相邻像素灰度差的平方和
//参考以上公式计算
for (int c = k; c < srcImg.rows - k; c++)
{//去掉外围的像素
for (int r = k; r < srcImg.cols - k; r++)
{
//定义灰度差平方和(y,x),注意是(y,x)不是(x,y)
//在使用image.at<TP>(x1, x2)来访问图像中点的值的时候,
//x1并不是图片中对应点的x轴坐标,而是图片中对应点的y坐标(也就是中的rows)
int V1 = 0, V2 = 0, V3 = 0, V4 = 0;
for (int i = -k; i <= k - 1; i++)
{
V1 += (srcImg.at<uchar>(c + i, r) - srcImg.at<uchar>(c + i + 1, r))*(srcImg.at<uchar>(c + i, r) - srcImg.at<uchar>(c + i + 1, r));
V2 += (srcImg.at<uchar>(c + i, r + i) - srcImg.at<uchar>(c + i + 1, r + i + 1))*(srcImg.at<uchar>(c + i, r + i) - srcImg.at<uchar>(c + i + 1, r + i + 1));
V3 += (srcImg.at<uchar>(c, r + i) - srcImg.at<uchar>(c, r + i + 1))*(srcImg.at<uchar>(c, r + i) - srcImg.at<uchar>(c, r + i + 1));
V4 += (srcImg.at<uchar>(c + i, r - i) - srcImg.at<uchar>(c + i + 1, r - i - 1))*(srcImg.at<uchar>(c + i, r - i) - srcImg.at<uchar>(c + i + 1, r - i - 1));
}
//找到最小值作为该点像素的兴趣值
float IV = min(min(V1, V2), min(V3, V4));
//存储(c,r)兴趣值
valueMat.at<float>(c, r) = IV;
}
}
//抑制局部最大且大于经验阈值的点作为候选点作为最终的特征点
//抑制窗口大小
int windowSize = restrainWinSize;
//去一半并int取整
int halfWindow = windowSize / 2;
for (int y = halfWindow; y < valueMat.rows - halfWindow; y += windowSize)
{//注意:要除去边界外围的像素(自己画个图理解一下),找到每个窗口的最大兴趣值的且大于阈值的像素的坐标
for (int x = halfWindow; x < valueMat.cols - halfWindow; x += windowSize)
{
//每个窗口兴趣值的最大值初值
float max = 0;
//判断像素是否被比较
bool Flag = 0;
//定义一个点来存储坐标
Point3f pt;
pt.x = -1;
pt.y = -1;
//使用Z值存贮兴趣值
pt.z = 0;
//计算以(y,x)为中心的windowSize*windowSize大小的窗口内部的局部极大值
for (int i = -halfWindow; i <= halfWindow; i++)
{
for (int j = -halfWindow; j <= halfWindow; j++)
{
float value;
//得到此点的兴趣值
value = valueMat.at<float>(y + i, x + j);
//如果大于最大值
if (value > max)
{
max = value;
pt.x = x + j;
pt.y = y + i;
pt.z = value;
Flag = 1;
}
}
}
//以(y,x)为中心的窗口计算完后
if (Flag == 1 && max >threshold)
{//存储特征点的坐标
featurePt.push_back(pt);
}
}
}
//绘制彩色特征点
string image_path = "u0369_panLeft.bmp";
//以RGB方式加载影像
Mat img_source = imread(image_path, IMREAD_COLOR);
//用圆和十字丝标出特征点
int radius = 4;//设置圆的半径
for (int i = 0; i < featurePt.size(); i++)
{//循环读特征点坐标
int xx = featurePt.at(i).x;
int yy = featurePt.at(i).y;
//画圆。参数CV_AA代表平滑,可以修改大小、粗细、颜色等属性。
circle(img_source, Point(xx, yy), radius, Scalar(0, 255, 255), 1, CV_AA);
//特征点标号
putText(img_source, to_string(i), Point(xx+2, yy-2), FONT_HERSHEY_SIMPLEX, 0.4, CV_RGB(255, 0, 0), 1.8, CV_AA);
//画十字丝
line(img_source, Point(xx - radius - 1, yy), Point(xx + radius + 1, yy), Scalar(0,255 , 255), 1, CV_AA);
line(img_source, Point(xx, yy - radius - 1), Point(xx, yy + radius + 1), Scalar(0,255, 255), 1, CV_AA);
}
//返回标记好的图像
return img_source;
}
- 评价:提取的特征点的在信息丰富的区域很集中,而贫乏区域几乎没有的特点,如最左边几乎没有特征点。
- 特征点提取需要控制特征点的密度,在整幅影像中按一定比例选取特征点,并将极值点周围的其他点去掉,这种方法选取的点集中在信息丰富的区域,而在信息贫乏的区域则没有点或很少点。因此为了控制特征点的密度,就需要调节 Moravec 算子中抑制窗口的大小,来减少极值点周围的其他点。
3.最终提取结果图
左影像:

四、均匀特征点提取
1.保持兴趣值窗口为 7,阈值设为 0,抑制窗口为 100 (很大就行,目的就是抑制完全周围一定范围的点,相当于画了格网一样),这种方法就相当于把整幅图像均匀分割成许多 100*100 的小图像,然后每个小图像里选取一个特征点。这种方法得到的特征点分布均匀,但是有些非特征点也会被提取出来(仅需修改上述代码的窗口、阈值等即可)。
2.结果图如下:

五、影像相关系数匹配
待续:基于Moravec算子的影像相关系数匹配:
匹配结果:

2021.12.25.
