数学基础篇
1 微分中值定理
1.1 罗尔中值定理
罗尔中值定理：如果 R 上的函数 f(x) 满足以下条件：（1）在闭区间 [a,b] 上连续，（2）在开区间 (a,b) 内可导，（3）f(a)=f(b)，则至少存在一个 ξ∈(a,b)，使得 f’(ξ)=0。
证明前:基于一个最大值最小值存在定理：闭区间连续函数一定存在最大值和最小值
证明：
证明：因为函数 f(x) 在闭区间[a,b] 上连续，所以存在最大值与最小值，分别用 M 和 m 表示，分两种情况讨论：
- 若 M=m，则函数 f(x) 在闭区间 [a,b] 上必为常函数，结论显然成立。
- 若 M>m，则因为 f(a)=f(b) 使得最大值 M 与最小值 m 至少有一个在 (a,b) 内某点ξ处取得，从而ξ是f(x)的极值点，又条件 f(x) 在开区间 (a,b) 内可导得，f(x) 在 ξ 处取得极值，由费马引理，可导的极值点一定是驻点，推知：f’(ξ)=0。
另证：若 M>m ，不妨设f(ξ)=M，ξ∈(a,b)，由可导条件知，f’(ξ+)<=0，f’(ξ-)>=0，又由极限存在定理知左右极限均为 0，得证。
通俗理解： 非常数函数情况下，f(a)=f(b) 所以在 (a,b) 内一定有一个波峰或者波谷，这个点的导数就是0；
1.2 拉格朗日中值定理
（1）在闭区间 [a,b] 上连续，（2）在开区间 (a,b) 内可导，（3）则至少存在一个 ξ∈(a,b)，使得f(a)-f(b)= f '(ξ)(b-a)成立。
证明：
ADD 推论：
（1）
（2）
1.3 柯西中值定理
和拉格朗日定理关系在于：
在柯西中值定理中，若取g(x)=x时，则其结论形式和拉格朗日中值定理的结论形式相同。
因此，拉格朗日中值定理为柯西中值定理的一个特例；反之，柯西中值定理可看作是拉格朗日中值定理的推广。
1.4 泰勒公式
当x0=0时，泰勒公式为麦克劳林公式
1.4.1 拉格朗日余项和佩亚诺余项
拉格朗日余项就是n阶泰勒余项
佩亚诺余项的展开如下：
最终可以看到两个余项如下：
1.4.2常见基本函数的泰勒公式—带佩亚诺余项（x–>0）
一些等价无穷小可以从泰勒公式里得出：
如
（1）：（1+x）a和1+ax等价无穷小（见上公式4）
（2）：ln(1+x)和x等价无穷小（见上公式5）
然后：ln(1+x)-x和(-1/2)x2等价无穷小（见上公式5，x左移）
1.4.3 泰勒公式余项的估计(拉格朗日余项)
应用可能性
（1）M很容易找到，或者很容易被估计
（2）x离x0越近，误差越小
（3）n越大，误差越小，所以需要泰勒多项式多展开几项
例子：
1.4.4常见基本函数的泰勒公式—带拉格朗日余项
2 导数的应用
2.1 极值问题
在应用数学，现实的问题很多都要转化为优化的问题，优化问题最终都是最值的问题，广泛进行可以优化的函数都是凸函数，很多问题最终都是归结于求极值问题。
什么是极值？：
2.1.1 费马定理
即：极值点的导数为0！！！
2.1.2 单调性和导数性质
某个导数为0的点的左右导数极性相反，这个点是极值点。
例子：
2.2函数的凹凸性
（1）凸函数的充分必要条件是：区间范围内，一阶导数单调上升
（2）凹函数则是区间范围内，一阶导数单调下降
从而推导出：
2.2.2 调和-几何-算术-平方-均值不等式
通过对数函数的凸性来证明
2.2.3 赫尔德不定式（）
该不等式证明：n维空间中的两个向量夹角余弦之绝对值不超过1。
2.3 渐近线
如何确定渐近线呢？
2、4 怎么绘制函数图像：
Python 数据结构篇（树）
1.树的基本介绍
1.1 定义
树（英语：tree）是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>=1）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
特点：
（1）每个节点有零个或多个子节点；
（2） 没有父节点的节点称为根节点；
（3）每一个非根节点有且只有一个父节点；
（4） 除了根节点外，每个子节点可以分为多个不相交的子树；
1.2 树的术语：
节点的度：一个节点含有的子树的个数称为该节点的度；
树的度：一棵树中，最大的节点的度称为树的度；
叶节点或终端节点：度为零的节点；
父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
兄弟节点：具有相同父节点的节点互称为兄弟节点；
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；
堂兄弟节点：父节点在同一层的节点互为堂兄弟；
节点的祖先：从根到该节点所经分支上的所有节点；
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
森林：由m（m>=0）棵互不相交的树的集合称为森林；
1.3 树的分类：
无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
（1）二叉树：每个节点最多含有两个子树的树称为二叉树；
完全二叉树：对于一颗二叉树，假设其深度为d(d>1)。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树，其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
平衡二叉树（AVL树）：当且仅当任何节点的两棵子树的高度差不大于1的二叉树；
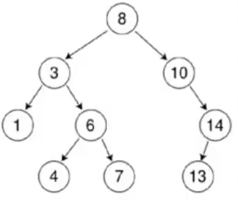
排序二叉树（二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树）；
平衡二叉树：这种左右子树的高度相差不超过 1 的树为平衡二叉树
排序二叉树：左子树和右子树保持恒定排序关系
（2）霍夫曼树（用于信息编码）：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
（3）B树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树。
2 二叉树：
2.1 二叉树定义：
性质1: 在二叉树的第i层上至多有2^(i-1)个结点（i>0）
性质2: 深度为k的二叉树至多有2^k - 1个结点（k>0）
性质3: 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外），如下图所示：
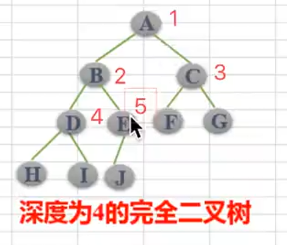
2.1 二叉树的实现（完全二叉树）
用队列的思想去实现广度优先遍历
如何实现：
（1）先入队root
（2) root出队，root.l为空则add,不空则入队，root.r为空则add,不空入队
（3）队内有root.l，root.r,先对root.l进行（2）一样的操作，没有add的话，对root.r进行（2）操作。一层层下去，直到找到空，然后add为止
"""节点类"""
class Node(object):
def __init__(self, elem=-1, lchild=None, rchild=None):
self.elem = elem
self.lchild = lchild
self.rchild = rchild
"""二叉树类--以完全二叉树为例"""
class Tree(object):
def __init__(self, root=None):
# 主根
self.root = root
# 完全二叉树的添加，满了就一层层往下走。从最左子树的度到最右子树的度（即广度优先遍历）
def add(self, elem):
# 从root出发，用队列的思想去处理广度优先遍历
node = Node(elem)
queue = []
if self.root is None:
self.root = node
else:
queue.append(self.root)
# 对已有的节点进行层次遍历
while queue:
cur = queue.pop()
if cur.lchild is None:
cur.lchild = node
return
elif cur.rchild is None:
cur.rchild = node
return
else:
# 如果左右子树都不为空，加入队列继续判断
queue.append(cur.lchild)
queue.append(cur.rchild)
2.2二叉树的遍历
那么树的两种重要的遍历模式是
广度优先遍历：广度优先一般用队列。
深度优先遍历：深度优先一般用递归，一般情况下能用递归实现的算法大部分也能用堆栈来实现。
2.2.1 广度优先遍历
2.2.2 深度优先遍历
链接：一篇关于深度优先遍历几种方法的动图介绍
（1）先序遍历（根节点->左子树->右子树）
（2）后序遍历（左子树->右子树->根节点）
（3）中序遍历（左子树->根节点->右子树）
实现（思路很简单，每一个最小二叉树都以遍历顺序进行操作）：
先序遍历（根节点->左子树->右子树）
# 先序遍历（根节点->左子树->右子树）
def preorder(self, root):
if root is None:
return
print(root.elem, end=" ")
self.preorder(root.lchild)
self.preorder(root.rchild)
中序遍历（左子树->根节点->右子树）
# 中序遍历（左子树->根节点->右子树）
def inorder(self, root):
if root is None:
return
self.inorder(root.lchild)
print(root.elem, end=" ")
self.inorder(root.rchild)
后序（左子树->右子树->根节点）
# 后序遍历（左子树->右子树->根节点）
def postorder(self, root):
if root is None:
return
self.inorder(root.lchild)
self.inorder(root.rchild)
print(root.elem, end=" ")
结果验证：
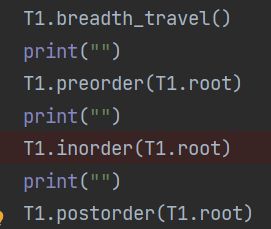得到
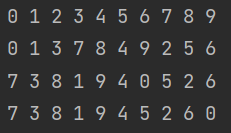对比通过：
2.2.3 反向推导树
（1）先序和中序数列推导树
（2）后序和中序数列推导树
