[人工智能]贝叶斯系列——贝叶斯定理、贝叶斯决策、朴素贝叶斯、贝叶斯网络、贝叶斯滤波器

写一个贝叶斯系列，整理一下贝叶斯定理、贝叶斯决策、朴素贝叶斯、贝叶斯网络、贝叶斯滤波器
众所周知，概率分为两个学派，频率学派（大数定理）和贝叶斯学派（贝叶斯公式），我们不去判断哪个学派说的更对，但是在实际生活中，由于我们获得的数据量实在有限，我们只能贝叶斯主义/经验主义地将采样到数据的频率当作概率（这并不符合大数定理，因为我们没有大数，所以这个我频率当概率并不是频率主义）
比如测试硬币正反的概率，如果我们做五次实验，五次都是正，那么频率学派直接当作正的概率是百分百，当然随着试验次数增加会修正。而贝叶斯学派则预先认为，概率是百分之五十，然后在测试的过程中慢慢修正，避免过大的偏差直接影响结果。

贝叶斯定理（公式）

$P(B|A)=\frac{P(B)P(A|B)}{P(A)}=\frac{P(B)P(A|B)}{{\sum }_{i=1}^{n}P(B_i)P(A|B_i)}$
$P(B_i|A)=\frac{P(B_i)P(A|B_i)}{P(A)}=\frac{P(B_i)P(A|B_i)}{{\sum }_{i=1}^{n}P(B_i)P(A|B_i)}$
这就是贝叶斯公式，分母是全概率公式$P(A)={\sum }_{i=1}^{n}P(B_i)P(A|B_i)$，这个应该懂吧。我坐车概率,走路概率0.5，坐车迟到概率0.1，走路迟到概率0.5，总的迟到概率0.5x0.1+0.5x0.5=0.3，很好理解吧。那么假设我已经迟到了，且知道我迟到的概率、坐车迟到概率与走路迟到概率，该如何推我是坐车来的，还是走路来的呢？这就是贝叶斯公式做的事情，由果推因。
其实不难不是吗，先回忆条件概率公式$P(B|A)=\frac{P(A,B)}{P(A)}$（你可以用这个式子推贝叶斯很好推，不需要记贝叶斯），条件概率公式应该符合直观感受吧，已知发生A的情况下发生B，那肯定分母是A发生的概率，分子是AB同时发生的概率呀。现在$P(A)$就是之前算的0.3，那么$P(A,B)$如何求呢？
把条件概率公式AB反一下，再乘过去就变成了$P(A,B)=P(B)?P(A|B)$了，带到之前分母里面，贝叶斯公式就出来了。
P(乘车|迟到)=P(乘车|迟到)/P(迟到），其实不难理解吧。

应用上的理解：
P(A)是被称为先验概率，这个是我们做实验可以得到的，连续一百天统计我迟到天数，迟到天数/总天数就是先验概率，这个我们每天在校门口等着统计就行了，很简单。我们知道小明离学校多远，一般几点起床，那很容易估算出他坐车迟到和走路迟到的概率。但我们实际上想知道的是他到底是走路来的还是坐车来的，我们不能派人每天监视他，这太麻烦了（对这个问题还算简单，在实际使用贝叶斯公式的时候，我们想采集到的数据可能根本无法直接测量）。所以我们使用贝叶斯公式进行估算，用相对容易获得的概率计算难以采样的数据。

这里其实有一个很大问题，就是我前面加粗的字，这个估算是我们通过生活经验随便给出的。但是对于机器学习来说，他并没有这些经验，所以后面的种种其实都是计算机如何通过数学学习出这个转移概率的过程。

朴素贝叶斯

这是一种最为简单的贝叶斯应用，做了一个假设，假设所有的条件都是独立的。
$P(B|A)=\frac{P(B)P(A|B)}{P(A)}=\frac{P(B){\prod }_{i}P(A_i|B)}{{\prod }_{i}P(A_i|B)}$
P(A)是统计出来的，但是可能有出现训练集中没有的A，朴素贝叶斯做的事情很简单，把所有没有出现的特征可能和出现的证据数量都+1，使得即使没有出现过的证据不会产生太大的影响。
事实上特征之间不可能完全独立，所以朴素贝叶斯是比较低级的模型。

贝叶斯决策

$P(B_i|A)=\frac{P(B_i)P(A|B_i)}{P(A)}$
我们回到基本的贝叶斯公式，我们假设我们现在已经知道了右边的所有信息，那我们就可以算出$P(B_i|A)$，那我们显而易见，我们选择使$P(B_i|A)$最大的$B_i$作为我们的预测结果。但是我们算出来的预测结果一般来说不是一个数字，而是一个分布（如果断言是一个数字的话，那很多没有采集到的样本概率都是0），既然是分布如何直接比较大小呢，概率论学的好的话都知道使用面积，我们希望预测正确的概率最大，也就是希望预测错误的概率最小，两个分布相交部分的面积就是分错的概率，我们希望这个面积最小。

但考虑一个用于分辨患者是否患病的模型，把有病当成没病，比反过来糟糕得多。所以我们给模型一个风险值，对于分类正确的情况，风险肯定是0，针对分错的情况应该有一个风险值乘概率，作为损失函数。我们决策的目标是使得这个值最小。

我的理解中，这个$\theta$既包含了模型的参数，也包含了决策的阈值。对于$\theta$如何求那就是优化算法的问题了比如我们熟知的牛顿法，但是概率中经常使用到一种叫最大期望（EM）的算法作为牛顿法的替代品。

贝叶斯网络

很简单，如下图所所示，相信看看就知道了，就是把各种随即变量之间的条件转移当左边，组成的有向无环图(DAG)，但是要计算出所有的情况，计算复杂程度是指数级的。
1.根据下面贝叶斯网络，表示 x1,…,x7 的完全联合概率分布。

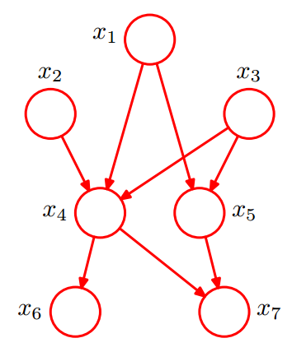
$$\begin{gathered} p(x_1,x_2,x_3,x_4,x_5,x_6,x_7) \\ =p(x_1)p(x_2)p(x_3)p(x_4|x_1,x_2,x_3)p(x_5|x_1,x_3)p(x_6|x_4)p(x_7|x_4,x_5) \end{gathered}$$

2. 基于课堂讲的防盗贝叶斯网络例子，求报警器没响，既没盗贼也没地震，两人都打电话的概率。
   

$$\begin{gathered} P(?B,?E,?A,J,M) \\ =P(?B)P(?E)P(?A|?B\wedge ?E)P(J|?A)P(M|?A) \\ =(1?0.001)(1?0.002)(1?0.001)?0.05?0.01 \\ \approx 4.98?10^{?4} \end{gathered}$$

贝叶斯滤波器

xx