前言
上篇记录了本质矩阵,基础矩阵,单应矩阵的求解。
本篇学习3D-2D点的匹配方法PnP(Perspective-n-Point),DLT,P3P。
PnP
已知某相邻帧之间匹配点的2D和3D坐标(世界坐标),求当前的位姿,称为PnP。
在这里,已知匹配点的3D坐标往往是上一帧的点坐标,2D坐标是当前帧与上一帧匹配到的点坐标。
DLT
直接线性变换(DLT)是直接通过相机运动模型求解。假设P是3D点,P’是2D点对应在归一化坐标平面的3D点
P
′
=
K
?
1
p
s
P
′
=
[
R
,
t
]
P
s
[
u
v
1
]
=
[
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
8
t
9
t
10
t
11
t
12
]
[
X
Y
Z
1
]
s
=
t
9
X
+
t
10
Y
+
t
11
Z
+
t
12
u
=
t
1
X
+
t
2
Y
+
t
3
Z
+
t
4
t
9
X
+
t
10
Y
+
t
11
Z
+
t
12
v
=
t
5
X
+
t
6
Y
+
t
7
Z
+
t
8
t
9
X
+
t
10
Y
+
t
11
Z
+
t
12
t
1
X
+
t
2
Y
+
t
3
Z
+
t
4
?
u
(
t
9
X
+
t
10
Y
+
t
11
Z
+
t
12
)
=
0
t
5
X
+
t
6
Y
+
t
7
Z
+
t
8
?
v
(
t
9
X
+
t
10
Y
+
t
11
Z
+
t
12
)
=
0
P' = K^{-1}p \\ sP'=[R,t]P \\ \quad \\ s\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} t_1 & t_2 & t_3 & t_4 \\ t_5 & t_6 & t_7 & t_8 \\ t_9 & t_{10} & t_{11} & t_{12} \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \\ \end{bmatrix} \\ s = t_9X + t_{10}Y + t_{11}Z + t_{12} \\ \quad \\ u = \frac {t_1X+t_2Y+t_3Z+t_4}{t_9X+t_{10}Y+t_{11}Z+t_{12}} \\ \quad \\ v = \frac {t_5X+t_6Y+t_7Z+t_8}{t_9X+t_{10}Y+t_{11}Z+t_{12}} \\ \quad \\ t_1X+t_2Y+t_3Z+t_4 - u(t_9X+t_{10}Y+t_{11}Z+t_{12}) = 0 \\ t_5X+t_6Y+t_7Z+t_8 - v(t_9X+t_{10}Y+t_{11}Z+t_{12}) = 0 \\
P′=K?1psP′=[R,t]Ps???uv1????=???t1?t5?t9??t2?t6?t10??t3?t7?t11??t4?t8?t12??????????XYZ1??????s=t9?X+t10?Y+t11?Z+t12?u=t9?X+t10?Y+t11?Z+t12?t1?X+t2?Y+t3?Z+t4??v=t9?X+t10?Y+t11?Z+t12?t5?X+t6?Y+t7?Z+t8??t1?X+t2?Y+t3?Z+t4??u(t9?X+t10?Y+t11?Z+t12?)=0t5?X+t6?Y+t7?Z+t8??v(t9?X+t10?Y+t11?Z+t12?)=0
由上面的方程可知,一对匹配点能形成两个方程,而位姿矩阵有12个未知数,因此6对匹配点就能通过矩阵方程
A
x
=
0
Ax=0
Ax=0求算位姿。
如果匹配点数多于6对,则方程编程超定方程组,可以使用线性最小二乘法求解(SVD),也就是把矩阵SVD分解 A = U Σ V T A=U\Sigma V^T A=UΣVT后, V V V的最后一个列向量是方程的解。
需要注意的是, A x = 0 , λ A x = 0 Ax=0,\lambda Ax=0 Ax=0,λAx=0,因此求出的 R , t R,t R,t也是没有尺度的,并且 R R R不一定满足正交矩阵约束。具体处理方法《十四讲》并没有详细说明。OpenCV内置了这个方法,因此这里也不展开。
P3P
P3P通过三对匹配点求位姿,再通过另外一对点验证结果,因此需要四对点,且四点不能共面。
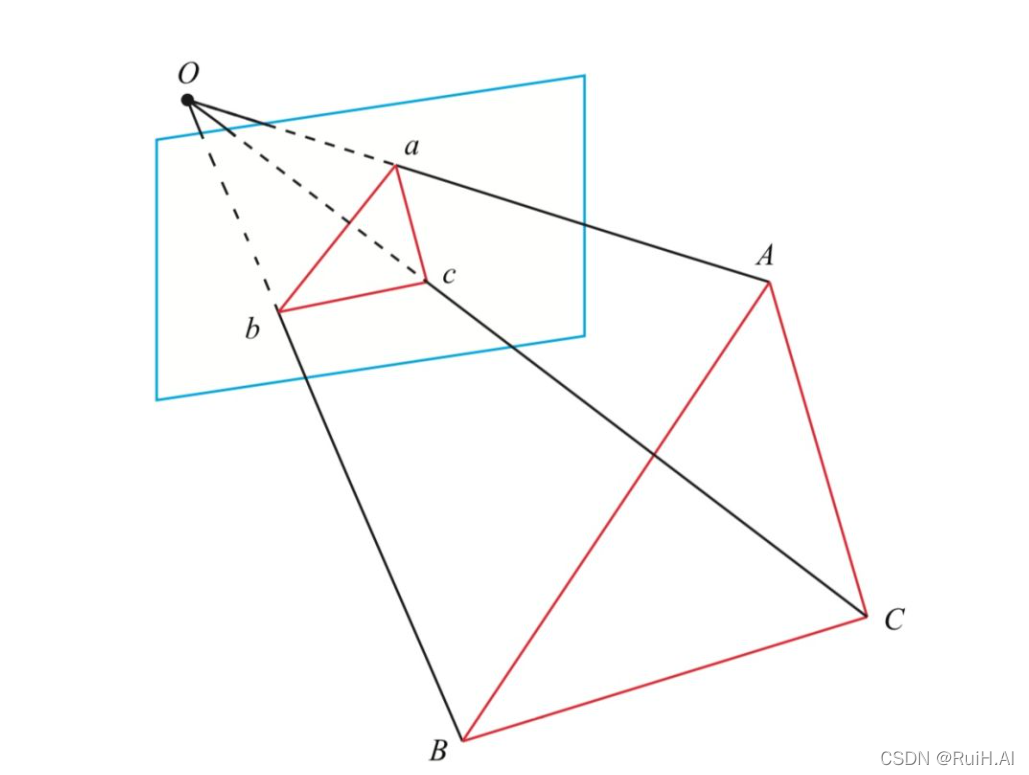
主要就是根据三角形Oab,OAB;Oac,OAC;Obc,OBC之间的相似,以及余弦定理,通过吴消元法计算出OA/OC,OB/OC,然后回代计算出OC。abc是归一化平面上的点。
余弦定理:
O
A
2
+
O
B
2
?
2
O
A
?
O
B
cos
?
A
O
B
=
A
B
2
O
B
2
+
O
C
2
?
2
O
B
?
O
C
cos
?
B
O
C
=
B
C
2
O
A
2
+
O
C
2
?
2
O
A
?
O
C
cos
?
A
O
C
=
A
C
2
OA^2+OB^2-2OA\cdot OB \cos AOB=AB^2 \\ OB^2+OC^2-2OB\cdot OC \cos BOC=BC^2 \\ OA^2+OC^2-2OA\cdot OC \cos AOC=AC^2 \\
OA2+OB2?2OA?OBcosAOB=AB2OB2+OC2?2OB?OCcosBOC=BC2OA2+OC2?2OA?OCcosAOC=AC2
上面的式子中,OA,OB,OC未知,AB,BC,AC已知,cos值都可以通过相似获得:
cos
?
A
O
B
=
cos
?
a
O
b
=
O
a
2
+
O
b
2
?
a
b
2
2
O
a
?
O
b
cos
?
B
O
C
=
cos
?
b
O
c
=
O
b
2
+
O
c
2
?
b
c
2
2
O
b
?
O
c
cos
?
A
O
C
=
cos
?
a
O
c
=
O
a
2
+
O
c
2
?
a
c
2
2
O
a
?
O
c
\cos AOB=\cos aOb=\frac {Oa^2+Ob^2-ab^2}{2Oa\cdot Ob} \\ \quad \\ \cos BOC=\cos bOc=\frac {Ob^2+Oc^2-bc^2}{2Ob\cdot Oc} \\ \quad \\ \cos AOC=\cos aOc=\frac {Oa^2+Oc^2-ac^2}{2Oa\cdot Oc} \\
cosAOB=cosaOb=2Oa?ObOa2+Ob2?ab2?cosBOC=cosbOc=2Ob?OcOb2+Oc2?bc2?cosAOC=cosaOc=2Oa?OcOa2+Oc2?ac2?
然后就能通过消元求出OA,OB,OC,也就得到了3D点的相机坐标,于是变成了3D-3D的问题,通过ICP解决。
P3P只能通过4对点计算位姿,误差比较大。OpenCV也内置了这个方法
后记
下篇记录BA,重头戏。