【1.2.2】版本 optimtool使用文档
版权归属:林景 (MIT Lisence)
pip install optimtool
相较于1.2.1版本的改变:
- 将Lasso问题求解的文件放在了example文件夹中
- 以后最优化的应用解法应该都放在example文件夹下
- unconstrain,constrain与hybrid用于更新底层算法,有好的可以加入,有不好的就删除。
1. 无约束优化算法性能对比
前五个参数完全一致,其中第四个参数是绘图接口,默认绘制单个算法的迭代过程;第五个参数是输出函数迭代值接口,默认为不输出。
method:用于传递线搜索方式
- from optimtool.unconstrain import gradient_descent
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 解方程得到精确解法(solve) | solve(funcs, args, x_0, draw=True, output_f=False, epsilon=1e-10, k=0) | gradient_descent.solve(funcs, args, x_0) |
| 基于Grippo非单调线搜索的梯度下降法 | barzilar_borwein(funcs, args, x_0, draw=True, output_f=False, method="grippo", M=20, c1=0.6, beta=0.6, alpha=1, epsilon=1e-10, k=0) | gradient_descent.barzilar_borwein(funcs, args, x_0, method=“grippo”) |
| 基于ZhangHanger非单调线搜索的梯度下降法 | barzilar_borwein(funcs, args, x_0, draw=True, output_f=False, method="ZhangHanger", M=20, c1=0.6, beta=0.6, alpha=1, epsilon=1e-10, k=0) | gradient_descent.barzilar_borwein(funcs, args, x_0, method=“ZhangHanger”) |
- from optimtool.unconstrain import newton
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 经典牛顿法 | classic(funcs, args, x_0, draw=True, output_f=False, epsilon=1e-10, k=0) | newton.classic(funcs, args, x_0) |
| 基于armijo线搜索方法的修正牛顿法 | modified(funcs, args, x_0, draw=True, output_f=False, method="armijo", m=20, epsilon=1e-10, k=0) | newton.modified(funcs, args, x_0, method=“armijo”) |
| 基于goldstein线搜索方法的修正牛顿法 | modified(funcs, args, x_0, draw=True, output_f=False, method="goldstein", m=20, epsilon=1e-10, k=0) | newton.modified(funcs, args, x_0, method=“goldstein”) |
| 基于wolfe线搜索方法的修正牛顿法 | modified(funcs, args, x_0, draw=True, output_f=False, method="wolfe", m=20, epsilon=1e-10, k=0) | newton.modified(funcs, args, x_0, method=“wolfe”) |
| 基于armijo线搜索方法的非精确牛顿法 | CG(funcs, args, x_0, draw=True, output_f=False, method="armijo", epsilon=1e-6, k=0) | newton.CG(funcs, args, x_0, method=“armijo”) |
| 基于goldstein线搜索方法的非精确牛顿法 | CG(funcs, args, x_0, draw=True, output_f=False, method="goldstein", epsilon=1e-6, k=0) | newton.CG(funcs, args, x_0, method=“goldstein”) |
| 基于wolfe线搜索方法的非精确牛顿法 | CG(funcs, args, x_0, draw=True, output_f=False, method="wolfe", epsilon=1e-6, k=0) | newton.CG(funcs, args, x_0, method=“wolfe”) |
- from optimtool.unconstrain import newton_quasi
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 基于BFGS方法更新海瑟矩阵的拟牛顿法 | bfgs(funcs, args, x_0, draw=True, output_f=False, method="wolfe", m=20, epsilon=1e-10, k=0) | newton_quasi.bfgs(funcs, args, x_0) |
| 基于DFP方法更新海瑟矩阵的拟牛顿法 | dfp(funcs, args, x_0, draw=True, output_f=False, method="wolfe", m=20, epsilon=1e-4, k=0) | newton_quasi.dfp(funcs, args, x_0) |
| 基于有限内存BFGS方法更新海瑟矩阵的拟牛顿法 | L_BFGS(funcs, args, x_0, draw=True, output_f=False, method="wolfe", m=6, epsilon=1e-10, k=0) | newton_quasi.L_BFGS(funcs, args, x_0) |
- from optimtool.unconstrain import trust_region
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 基于截断共轭梯度法的信赖域算法 | steihaug_CG(funcs, args, x_0, draw=True, output_f=False, m=100, r0=1, rmax=2, eta=0.2, p1=0.4, p2=0.6, gamma1=0.5, gamma2=1.5, epsilon=1e-6, k=0) | trust_region.steihaug_CG(funcs, args, x_0) |
import sympy as sp
import matplotlib.pyplot as plt
from optimtool.unconstrain import gradient_descent, newton, newton_quasi, trust_region
f, x1, x2, x3, x4 = sp.symbols("f x1 x2 x3 x4")
f = (x1 - 1)**2 + (x2 - 1)**2 + (x3 - 1)**2 + (x1**2 + x2**2 + x3**2 + x4**2 - 0.25)**2
funcs = sp.Matrix([f])
args = sp.Matrix([x1, x2, x3, x4])
x_0 = (1, 2, 3, 4)
# 无约束优化测试函数性能对比
f_list = []
title = ["gradient_descent_barzilar_borwein", "newton_CG", "newton_quasi_L_BFGS", "trust_region_steihaug_CG"]
colorlist = ["maroon", "teal", "slateblue", "orange"]
_, _, f = gradient_descent.barzilar_borwein(funcs, args, x_0, False, True)
f_list.append(f)
_, _, f = newton.CG(funcs, args, x_0, False, True)
f_list.append(f)
_, _, f = newton_quasi.L_BFGS(funcs, args, x_0, False, True)
f_list.append(f)
_, _, f = trust_region.steihaug_CG(funcs, args, x_0, False, True)
f_list.append(f)
# 绘图
handle = []
for j, z in zip(colorlist, f_list):
ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()
图像:

2. 非线性最小二乘问题
- from optimtool.unconstrain import nonlinear_least_square
method:用于传递线搜索方法
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 基于高斯牛顿法的非线性最小二乘问题解法 | gauss_newton(funcr, args, x_0, draw=True, output_f=False, method="wolfe", epsilon=1e-10, k=0) | nonlinear_least_square.gauss_newton(funcr, args, x_0) |
| 基于levenberg_marquardt的非线性最小二乘问题解法 | levenberg_marquardt(funcr, args, x_0, draw=True, output_f=False, m=100, lamk=1, eta=0.2, p1=0.4, p2=0.9, gamma1=0.7, gamma2=1.3, epsilon=1e-10, k=0) | nonlinear_least_square.levenberg_marquardt(funcr, args, x_0) |
import sympy as sp
import matplotlib.pyplot as plt
from optimtool.unconstrain import nonlinear_least_square
r1, r2, x1, x2 = sp.symbols("r1 r2 x1 x2")
r1 = x1**3 - 2*x2**2 - 1
r2 = 2*x1 + x2 - 2
funcr = sp.Matrix([r1, r2])
args = sp.Matrix([x1, x2])
x_0 = (2, 2)
f_list = []
title = ["gauss_newton", "levenberg_marquardt"]
colorlist = ["maroon", "teal"]
_, _, f = nonlinear_least_square.gauss_newton(funcr, args, x_0, False, True) # 第五参数控制输出函数迭代值列表
f_list.append(f)
_, _, f = nonlinear_least_square.levenberg_marquardt(funcr, args, x_0, False, True)
f_list.append(f)
# 绘图
handle = []
for j, z in zip(colorlist, f_list):
ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()
图示:
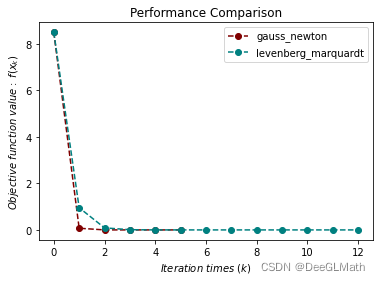
3. 等式约束优化测试
- from optimtool.constrain import equal
无约束内核默认采用wolfe线搜索方法
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 二次罚函数法 | penalty_quadratic(funcs, args, cons, x_0, draw=True, output_f=False, sigma=10, p=2, epsilon=1e-4, k=0) | equal.penalty_quadratic(funcs, args, cons, x_0) |
| 增广拉格朗日法 | lagrange_augmented(funcs, args, cons, x_0, draw=True, output_f=False, lamk=6, sigma=10, p=2, etak=1e-4, epsilon=1e-6, k=0) | equal.lagrange_augmented(funcs, args, cons, x_0) |
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from optimtool.constrain import equal
f, x1, x2 = sp.symbols("f x1 x2")
f = x1 + np.sqrt(3) * x2
c1 = x1**2 + x2**2 - 1
funcs = sp.Matrix([f])
cons = sp.Matrix([c1])
args = sp.Matrix([x1, x2])
x_0 = (-1, -1)
f_list = []
title = ["penalty_quadratic", "lagrange_augmented"]
colorlist = ["maroon", "teal"]
_, _, f = equal.penalty_quadratic(funcs, args, cons, x_0, False, True) # 第四个参数控制单个算法不显示迭代图,第五参数控制输出函数迭代值列表
f_list.append(f)
_, _, f = equal.lagrange_augmented(funcs, args, cons, x_0, False, True)
f_list.append(f)
# 绘图
handle = []
for j, z in zip(colorlist, f_list):
ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()
图示:
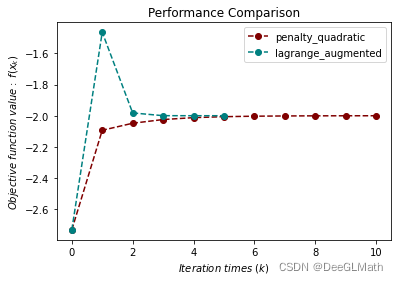
4. 不等式约束优化测试
- from optimtool.constrain import unequal
无约束内核默认采用wolfe线搜索方法
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 二次罚函数法 | penalty_quadratic(funcs, args, cons, x_0, draw=True, output_f=False, sigma=1, p=0.4, epsilon=1e-10, k=0) | unequal.penalty_quadratic(funcs, args, cons, x_0) |
| 内点(分式)罚函数法 | penalty_interior_fraction(funcs, args, cons, x_0, draw=True, output_f=False, sigma=12, p=0.6, epsilon=1e-6, k=0) | unequal.penalty_interior_fraction(funcs, args, cons, x_0) |
import sympy as sp
import matplotlib.pyplot as plt
from optimtool.constrain import unequal
f, x1, x2 = sp.symbols("f x1 x2")
f = x1**2 + (x2 - 2)**2
c1 = 1 - x1
c2 = 2 - x2
funcs = sp.Matrix([f])
cons = sp.Matrix([c1, c2])
args = sp.Matrix([x1, x2])
x_0 = (2, 3)
f_list = []
title = ["penalty_quadratic", "penalty_interior_fraction"]
colorlist = ["maroon", "teal"]
_, _, f = unequal.penalty_quadratic(funcs, args, cons, x_0, False, True) # 第四个参数控制单个算法不显示迭代图,第五参数控制输出函数迭代值列表
f_list.append(f)
_, _, f = unequal.penalty_interior_fraction(funcs, args, cons, x_0, False, True)
f_list.append(f)
# 绘图
handle = []
for j, z in zip(colorlist, f_list):
ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()
图示:
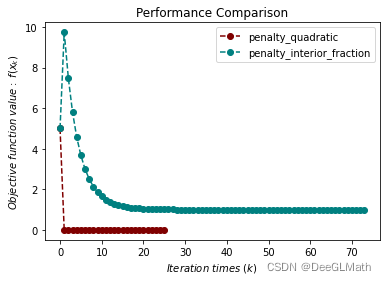
5. 混合等式约束测试
- from optimtool.constrain import mixequal
无约束内核默认采用wolfe线搜索方法
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 二次罚函数法 | penalty_quadratic(funcs, args, cons_equal, cons_unequal, x_0, draw=True, output_f=False, sigma=1, p=0.6, epsilon=1e-10, k=0) | mixequal.penalty_quadratic(funcs, args, cons_equal, cons_unequal, x_0) |
| L1罚函数法 | penalty_L1(funcs, args, cons_equal, cons_unequal, x_0, draw=True, output_f=False, sigma=1, p=0.6, epsilon=1e-10, k=0) | mixequal.penalty_L1(funcs, args, cons_equal, cons_unequal, x_0) |
| 增广拉格朗日函数法 | lagrange_augmented(funcs, args, cons_equal, cons_unequal, x_0, draw=True, output_f=False, lamk=6, muk=10, sigma=8, alpha=0.5, beta=0.7, p=2, eta=1e-3, epsilon=1e-4, k=0) | mixequal.lagrange_augmented(funcs, args, cons_equal, cons_unequal, x_0) |
import sympy as sp
import matplotlib.pyplot as plt
from optimtool.constrain import mixequal
f, x1, x2 = sp.symbols("f x1 x2")
f = (x1 - 2)**2 + (x2 - 1)**2
c1 = x1 - 2*x2
c2 = 0.25*x1**2 - x2**2 - 1
funcs = sp.Matrix([f])
cons_equal = sp.Matrix([c1])
cons_unequal = sp.Matrix([c2])
args = sp.Matrix([x1, x2])
x_0 = (0.5, 1)
f_list = []
title = ["penalty_quadratic", "penalty_L1", "lagrange_augmented"]
colorlist = ["maroon", "teal", "orange"]
_, _, f = mixequal.penalty_quadratic(funcs, args, cons_equal, cons_unequal, x_0, False, True) # 第四个参数控制单个算法不显示迭代图,第五参数控制输出函数迭代值列表
f_list.append(f)
_, _, f = mixequal.penalty_L1(funcs, args, cons_equal, cons_unequal, x_0, False, True)
f_list.append(f)
_, _, f = mixequal.lagrange_augmented(funcs, args, cons_equal, cons_unequal, x_0, False, True)
f_list.append(f)
# 绘图
handle = []
for j, z in zip(colorlist, f_list):
ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()
图示:

6. Lasso问题测试
- from optimtool.example import Lasso
| 方法 | 函数参数 | 调用示例 |
|---|---|---|
| 梯度下降法 | gradient_descent(A, b, mu, args, x_0, draw=True, output_f=False, delta=10, alp=1e-3, epsilon=1e-2, k=0) | Lasso.gradient_descent(A, b, mu, args, x_0,) |
| 次梯度算法 | subgradient(A, b, mu, args, x_0, draw=True, output_f=False, alphak=2e-2, epsilon=1e-3, k=0) | Lasso.subgradient(A, b, mu, args, x_0,) |
min
?
1
2
∣
∣
A
x
?
b
∣
∣
2
+
μ
∣
∣
x
∣
∣
1
\min \frac{1}{2} ||Ax-b||^2+\mu ||x||_1
min21?∣∣Ax?b∣∣2+μ∣∣x∣∣1?
给定
A
m
×
n
A_{m \times n}
Am×n?,
x
n
×
1
x_{n \times 1}
xn×1?,
b
m
×
1
b_{m \times 1}
bm×1?,正则化常数
μ
\mu
μ。解决该无约束最优化问题,该问题目标函数一阶不可导。
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from optimtool.example import Lasso
import scipy.sparse as ss
f, A, b, mu = sp.symbols("f A b mu")
x = sp.symbols('x1:9')
m = 4
n = 8
u = (ss.rand(n, 1, 0.1)).toarray()
A = np.random.randn(m, n)
b = A.dot(u)
mu = 1e-2
args = sp.Matrix(x)
x_0 = tuple([1 for i in range(8)])
f_list = []
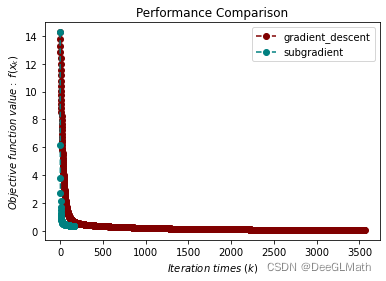
title = ["gradient_descent", "subgradient"]
colorlist = ["maroon", "teal"]
_, _, f = Lasso.gradient_descent(A, b, mu, args, x_0, False, True, epsilon=1e-4)# 第四个参数控制单个算法不显示迭代图,第五参数控制输出函数迭代值列表
f_list.append(f)
_, _, f = Lasso.subgradient(A, b, mu, args, x_0, False, True)
f_list.append(f)
# 绘图
handle = []
for j, z in zip(colorlist, f_list):
ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()
图示: