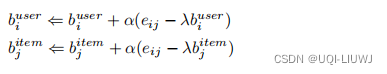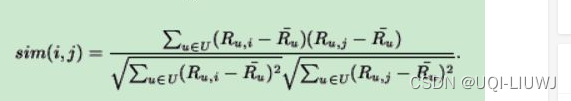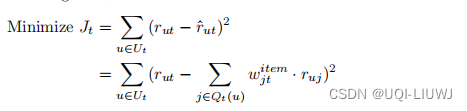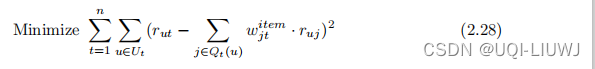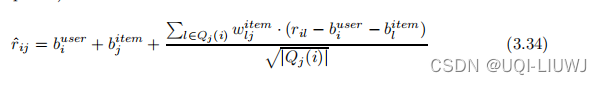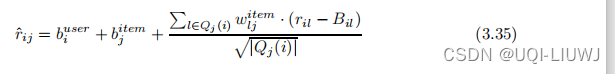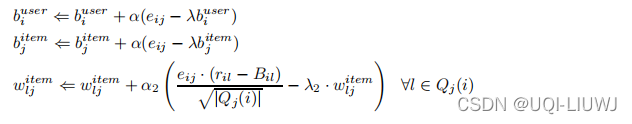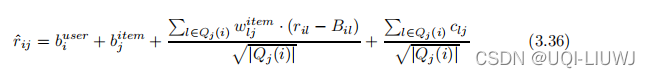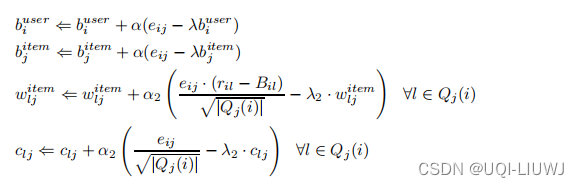????????由于其启发式性质，基于邻域的方法通常被认为与其他优化模型具有内在的不同。 尽管如此，结果表明基于邻域的方法也可以嵌入在其他优化模型的上下文中。 这是一个相当方便的框架，因为它为邻域模型与其他优化模型（例如潜在因子模型）的集成铺平了道路。
? ? ? ? 在本节中，我们假设评分矩阵 R 以均值为中心。 换句话说，评分矩阵的全局平均值 μ 已经从所有条目中减去，并且所有预测都将在以平均值为中心的值上执行。 全局平均值 μ 可以在后处理阶段加回到预测值中。?
? ? ? ? 同时，我们还是令S表示所有有观测值的(i,j)对的集合
?
1 非个性化的、以偏差为中心的模型
推荐系统笔记：无任何限制的矩阵分解_UQI-LIUWJ的博客-CSDN博客
????????非个性化的、以偏差为中心的模型预测 R 中的（以平均值为中心的）评级，纯粹是作为用户和项目偏差的叠加。
???????? 换句话说，评分完全由用户的慷慨度和项目的受欢迎程度来解释，而不是用户对项目的特定个性化兴趣。
???????? 令
为用户i 的偏差变量，
为项目j 的偏差变量。 那么，本小节介绍的模型的预测如下：
????????
? ? ? ? 我们的目标函数为：（带正则项之后）
? ? ? ? ?同样地，可以使用梯度下降解决这个优化问题
????????有趣的是，尽管具有非个性化的性质，但纯粹以偏差为中心的模型通常可以提供合理的预测。当评级数据量有限时尤其如此。求解
设置为(i,j)条目的预测值。
???????因此，集成模型求解的第一步是通过求解非个性化模型来确定常数值
值的粗略基准估计。
????????通常，将每个有观测值的条目
?
2?模型的邻域部分
2.1 用 回归的角度看邻域
????????我们认为，同一个用户的不同打过分的item之间存在着某些关联性。比如某件商品的打分，可以有和它最相似的同一用户对其他几件商品的打分加权求和得到。
?????????Qt(u) 中的相似项可以通过修正余弦相似度来衡量 （也就是这个用户对项目i的打分-这个用户的平均打分，这个的余弦值）
????????集合 Qt(u) 表示目标项目 t 的 k 个最相似的项的子集。（不一定正好是k个）
? ? ? ? 注意一点是，Qt(u)即使对于同一个项目t，不同的用户也会有不同的结果；但是衡量的是两个项目之间的关联度，和哪个用户是没有关系的！
? ? ? ? 所以对某一个项目t，我们记给它打过分的用户的集合为
,那么这个项目的目标函数为
?????????
? ? ? ? 所有这个项目的实际打分和预测打分（通过近邻回归来预测）之间的差距
? ? ? ? ?需要注意的是，此优化问题是针对每个目标项 t 单独制定的。
????????然而，可以将不同目标项 t 的目标函数相加，对优化解决方案没有区别，因为各个目标函数中的未知系数
在不同t值上不重叠 ∈ {1 ...n}。 因此，我们有以下合并公式：
?
? ? ? ? ?反之亦可，还可以以分解形式解决每个较小的优化问题（即目标函数 Jt），而不会影响整体的解决方案。
????????引入合并公式的优点是可以与其他优化模型相结合，例如矩阵分解方法
?2.2? 将邻域与偏差结合
我们有：?
?可以想成?
?，就和前面的邻域回归差不多了，唯一的区别就是这个分母的系数，这是一个启发式的系数
?????????倘若我们用第一小节的方法 将右边的
?替换成?
????????此时剩下的?
和
就是需要被优化的参数
于是此时带正则项的目标函数为：?
令
那么此时我们对上述目标函数进行梯度下降，
?2.3?引入项-项隐式反馈变量
?????????通过引入项-项隐式反馈变量
，可以通过隐式反馈进一步增强该邻域模型。
???????? 基本思想是，如果项目 j 与许多相邻项目被同一用户 i 一起评分，那么这些相邻项与项目j之间的关联程度 应该对预测评分
产生影响。
???????? 这种影响与 j 的这些相邻项目的评分的实际值无关。
? ? ? ? 这种影响等于
?（分母还是那个启发式系数）
?于是，此时带有邻域、偏差、用户隐式反馈变量的模型可以写作：
?同样地，也可以对各项进行梯度下降操作
?
