[人工智能]模板匹配——弹性匹配

弹性匹配

基本概念

对于人脸匹配，可将人脸看做非刚性模型来匹配人脸结构。对该系统进行训练，采用人工标定人脸特征点，用局部特征描述方法（如Gabor jets）来提取每个特征点的特征。在多人中抽取这些特征点，可得到一种不变性规律——弹性串图，用于表示非刚性或者可变形事物。比较一个传图和新的人脸图像，采用迭代法找到每个弹性图特征点位置和特征之间的最小距离，即为弹性图匹配。

在人脸姿态估计中，对每个姿势建立一个弹性图。输入新的人脸图像，将其与弹性图进行匹配，找到最大的匹配结果，作为该图的姿态。优点：采用弹性图匹配能够得到更加相似的结果；不足：姿态是离散的，因此需要很多弹性图来得到更合适的人脸姿态估计，其算法的时间复杂度也高。一个简单的人脸检测与识别系统如下：

Gabor滤波

Jets的定义

Gabor小波是以任意一个高斯函数作为窗函数的波函数。一个图像像素与不同方向和频率的 Gabor 核卷积后的系数集合称为一个 Jet。一个 jet 描述了图像 $I(x)$ 给定图像 $x=(x,y)$ 周围的一小块灰度值基于小波变换所得到的。
定义卷积为：$J_j(x)=\int I(x^{\prime })?{\Psi }_j(x?x)d^2{x}^{\prime }$，

Gabor 核函数为： Ψ j ( x ? ) = ∣ ∣ k j ? ∣ ∣ 2 σ 2 ? e x p { ? ∣ ∣ k j ? ∣ ∣ 2 ? ∣ ∣ x ? ∣ ∣ 2 2 σ 2 } ? [ e x p { i k j ? x ? } ? e x p { ? σ 2 2 } ] \displaystyle \Psi_j(\vec x)=\frac{||\vec {k_j}||^2}{\sigma^2}\cdot exp\{-\frac{||\vec {k_j}||^2\cdot||\vec x||^2}{2\sigma^2}\}\cdot[exp\{i\vec {k_j}\vec x\}-exp\{-\frac{\sigma^2}{2}\}] Ψj?(x )=σ2∣∣kj? ?∣∣2??exp{?2σ2∣∣kj? ?∣∣2?∣∣x ∣∣2?}?[exp{ikj? ?x }?exp{?2σ2?}]，

其中波矢量为：$k_j=\left(\begin{array}{c}{k}_{jx}\\ k_{jy}\end{array}\right)=\left(\begin{array}{c}{k}_v?cos{\phi }_u\\ k_v?sin{\phi }_u\end{array}\right)$，其中 $k_v=2^{\frac{v+2}{2}}?\pi ,{\phi }_v=u?\pi /8$，其中频率系数 $v=0,?,4$；方向系数 $u=0,?,7$，这样形成40个相关系数来描述灰度图像中 x 点附近领域的特征。

而一个 Jet 定义为从每个像素点获得的40个复系数组成的集合 { J j } \{J_j\} {Jj?}，即 $J_j=a_j?e^{i{?}_j}$，其中 $a_j$ 为复系数的幅值，${?}_j$ 为复系数的相位，一个特征值就是一组系数 { J j } \{J_j\} {Jj?}，两个 Jets 之间的相似性可以定义为：

$S_a(J,J^{\prime })=\frac{{\sum }_{j=1}^N{a}_j?a_j^{\prime }}{\sqrt{{\sum }_{j=1}^N{a}_j^2}?{\sum }_{j=1}^N{a^{\prime }}_j^2}$，其中 N 代表 Gabor滤波器的个数。

使用Gabor小波的原因

Gabor小波变换核函数具有与人类大脑皮层简单细胞的二维反射区相同的特性，即能够捕捉到对应于空间频率（尺度）、空间位置及方向选择性的局部结构信息，被广泛地应用于图像分析和理解。Gabor 小波的特性使得其对于亮度和人脸表情的变化不敏感，对人脸识别有利。

相关的三幅图

1.首先定义好一幅人脸标号图，标号图的节点由先前选择好的脸部特征点组成，这些特征点选择在那些容易区分不同脸的位置。

2.将Gabor滤波在每一个特征点上的响应称之为 jet，将包含相应 jets的标号图称为人脸图，用来对人脸进行描述。

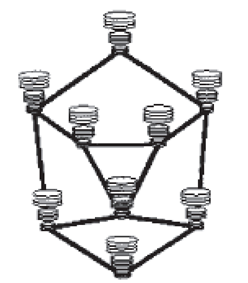
3.对于每个节点，将其特征点的位置以及相应的 jet 进行存储，用节点与节点之间的距离来标定标号图的边缘。对于新的人脸图像，要自动定位特征点时，系统需要对普通人脸有一个代表性的描述。该描述需要涵盖具有较广相貌特征范围的人脸图像（如各种形状特征的眼睛、鼻子、嘴巴、胡须形状、肤色等）。

这一点的实现，要使用一批具有代表性的人脸标号图复合成人脸束图（the face bunch graph，FBG），每一个标号图有着同样的结构以及特征点人脸束图中：每一个节点为多个人脸标号图的对应节点的 Gabor 小波变换系数的集合，其每一条边为多个人脸标号图的对应边的平均。通过这样的方式，FBG则对各种人脸都具有代表性的描述。

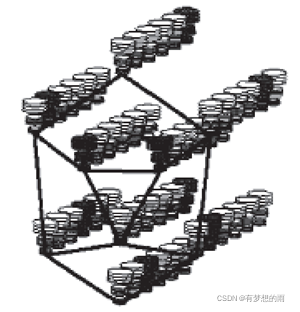
由于人脸束图的构建是在离线状态下进行的，所以可通过手工方式确定用于构建人脸束图的人脸图像的特征点的位置。

步骤

1.创建人脸弹性束图

首先，需要一组模板图，提取模板图上每个特征点位置信息和特征值，并将其存储在人脸弹性束图结构中。人脸弹性束图可以看做是一个描述特征点的数据库，包含了平均的人脸信息，在新的人脸图定位特征点时，用作参考模板。

标准的人脸弹性属兔包含的特征点有：左眼、右眼、鼻梁、左眼眉、右眼眉、左眼内角、右眼内角、左眼外角、右眼外角、鼻尖、中鼻根、左鼻根、右鼻根、上嘴唇、下嘴唇、左嘴角、右嘴角、额头、额头左侧、额头右侧、左脸颊、右脸颊、下巴等。

模板图是经过预处理的人脸图，它包含了当前图上特征点的位置信息。在创建弹性束图使，按照模板图提供的特征点信息位置，通过 Gabor 小波滤波，得到对应的特征值。所有模板图的特征值都存储到人脸弹性束图中，该结构包含了人脸上的每一个特征点及其对应的一系列特征值。

2.创建人脸图

人脸图是用来表示人脸特征的数据结构，每一幅人脸都可以用一个人脸图来表示。人脸图包含了人脸的每一个特征点的位置信息以及该特征点所对应的特征值。

首先，确定特征点的位置——特征点的定位，两步：
A. 通过人脸弹性束图得到的平均人脸信息粗略估计特征点的大概位置；
B. 提取粗略估计位置处的特征值，与人脸弹性束图中的特征值比较以获得更准确的位置估计。然后，通过Gabor小波变换提取特征值。所有的特征信息构成一个人脸图。

搜索步骤：
（1）对每个特征点，从已知的FBG中位置信息定位每个特征点的粗略位置 $(x_n,y_n)$；
（2）在以标准化的人脸图像中计算出 $(x_n,y_n)$ 处的Gabor变换向量系数 $J_n$；
（3）将 $J_n$ 与FBG中该特征点的系数 $J^{Bm}$比较（m为聚集特征点束的数量），其中相似度最高的候选者为 $J_n^{\prime }$，计算其位置误差（即两者的欧式距离） $d_n=J_n^{\prime }?J_n$，则特征点的精确位置修正为：$(x_n^{\prime },y_n^{\prime })=(x_n,y_n)+d_n$；
（4）反复第一步到第三部，可得到一副人脸图像上多个特征点的精确位置 $(x_n^{\prime },y_n^{\prime })$，对应这些点求出其Gabor系数。

这样一副人脸图形FBG就可以用 n 个特征点的 Gabor 系数来表示人脸图像。

3.匹配

对 Jets 之间的相似度进行估计，然后将所有节点的相似性进行平均化，若采用Gabor滤波相应模型，则为: $L(G,G^{\prime })=\frac{1}{n}\sum _{i=1}{S}_a(J_i,J_i^{\prime })$，其中，$J_i,J_i^{\prime }$分布为图像 $G,G^{\prime }$ 的第 i 个 Jets，n代表每一个人脸标号图的节点个数。

相似度量

使用以下度量，在FBG中找出与测试图像最相似的一个人脸描述图，

$S_B(G^I,B)=\frac{1}{N}\sum _n{max}_m(S_a(J_n^I,J_n^{Bm}))?\frac{\lambda }{E}\sum _e\frac{(△x_e^I?△x_e^B{)}^2}{(△x_e^B{)}^2}$

其中，第二项用于描述标号图 $G^I$ 与束图 $B$ 对应边的相似度量，图的边 $x_e$ 由两节点间的空间位置决定，即 $△x_e=x_n?x_n^{\prime },e=1,?,E$；而 $\lambda$ 用于决定局部特征点相似度的空间位置相似度两者的重要性，即调节两项的权重，需提供实验方法确定。