[人工智能]利用两层Fully-Connected网络对CIFAR-10数据集进行分类

??前面已经在简单神经网络的实现中实现了一个两层的Fully-Connected网络实现了手写数字的识别。在那篇文章中我们使用了sigmoid函数作为激活函数，以逻辑回归的损失函数作为网络的损失函数。另一方面，我们在那篇文章的推导较为复杂。另外，我们也没有进行矩阵化处理，并没有对程序的性能得到改善。
??在这篇文章中，将重新介绍FC网络，使用最近常见的激活函数ReLU，损失函数以改为了softmax；我们已将以一种更好理解和更加一般的方式取理解神经网络的前向和后向传播；最后，我们的代码也进行了矩阵化(vectorized)处理。

前向传播和后向传播

一个神经网络的工作原理实际上就是复合函数。而前向传播就是复合函数的计算。如下图所示：

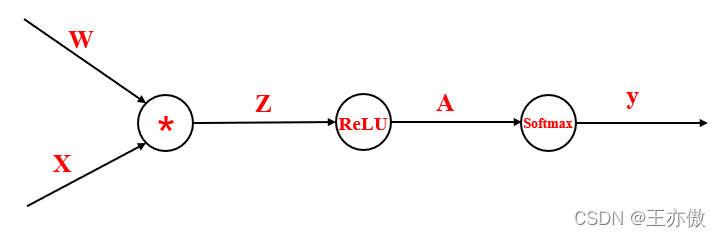
由于我们要通过损失函数最优化权重$W$，所以我们可以认为损失函数是一个关于权重$W$的函数。我们为了方便解释，我们将上图乘法看做函数$f$,ReLU函数看做函数$g$,Softmax函数为$h$。所以有$y=h(g(f(W)))$。
??对于前向传播，我们只需要一步一步计算复合函数即可，例如先计算$Z=f(W)$,再计算$A=g(Z)$,最后计算得到结果$y=h(A)$。
??对于后向传播，实际上就是计算每一步的梯度。对于复合函数的梯度计算，我们自然想到链式法则。比如，我们想计算损失函数$y$对权重W的梯度，这样就有：
$$\frac{?y}{?W}=\frac{?y}{?Z}\frac{?Z}{?W}$$
也就是说计算损失函数$y$对权重W的梯度$\frac{?y}{?W}$,我们需要计算$\frac{?y}{?Z}$和$\frac{?Z}{?W}$。而$Z$和$W$之间的直接由函数$f$联系，所以可以直接计算梯度。而对于$\frac{?y}{?Z}$可以认为是从上层传开的梯度，它和$W$无关，可以写为：
$$\frac{?y}{?Z}=\frac{?y}{?A}\frac{?A}{?Z}$$
也就是说计算$\frac{?y}{?Z}$，首先要计算$\frac{?A}{?Z}$，而$A$和$Z$之间直接由函数$g$联系，可以直接计算得到。最后，$\frac{?y}{?A}$同样是从上层传递而来。
??为了更好地表述，我们定义上面的层传递而来的梯度为上游梯度（Upstream gradient）。而每一层自己在局部计算两个变量之间直接由一个函数联系叫做局部梯度。例如：对于$\frac{?y}{?W}=\frac{?y}{?Z}\frac{?Z}{?W}$，$\frac{?Z}{?W}$为局部梯度，$\frac{?y}{?Z}$为上游梯度；$\frac{?y}{?Z}=\frac{?y}{?A}\frac{?A}{?Z}$，$\frac{?A}{?Z}$为局部梯度，$\frac{?y}{?A}$为上游梯度。而$\frac{?y}{?W}$的上游梯度$\frac{?y}{?Z}$就是上一层的梯度。
??所以对于复杂、层数较多的复合函数，我们能通过这种方法计算：每一步关于目标函数的梯度为上面的层传来的梯度（也就上一层关于目标函数的梯度）乘上这一层自己的局部梯度。这个过程我们可以认为是每一层将自己的信息传递给前面的层。
下图是一个简单的例子：

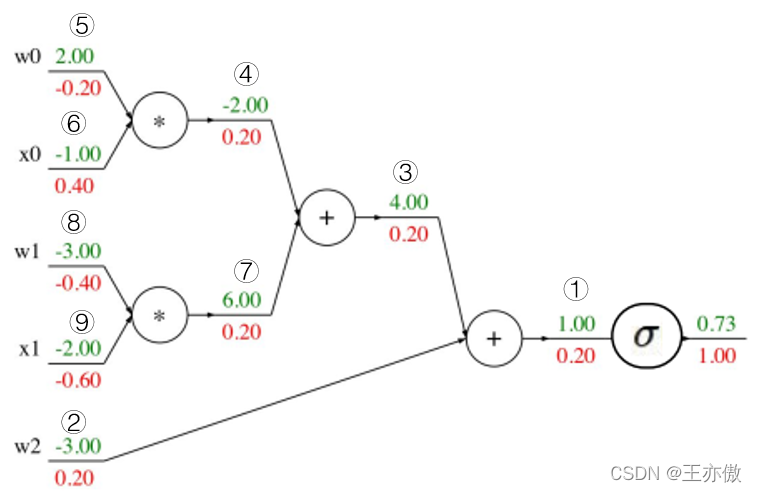
绿色的每一层的值，红色的时每一层的梯度。这里须注意的是，最上层由于其没有再往上的层，所以我们可以认为其上游梯度为1。下面介绍几层进行介绍，剩余的层可以通过相同的道理得到：
①: 其上游梯度为1，局部梯度为${\sigma }^{{}^{\prime }}(1)$。所以${\sigma }^{{}^{\prime }}(1)?1=0.2$,这里$\sigma$为sigmoid函数;
②: 对于w2的梯度：由于$?(w2+result③)/?w2=1$,而上一层的梯度为0.2，所以w2的梯度为$1?0.2$;
③: 和②同理，这一层的局部梯度为1，上一层的梯度为0.2，所以梯度依然为0.2;
⑤: $?(w2?result⑥)/?w2=?1$，上一层的梯度为0.2，所以梯度为0.2*-1=-0.2。
下面介绍几种常见的运算的梯度传递方式：

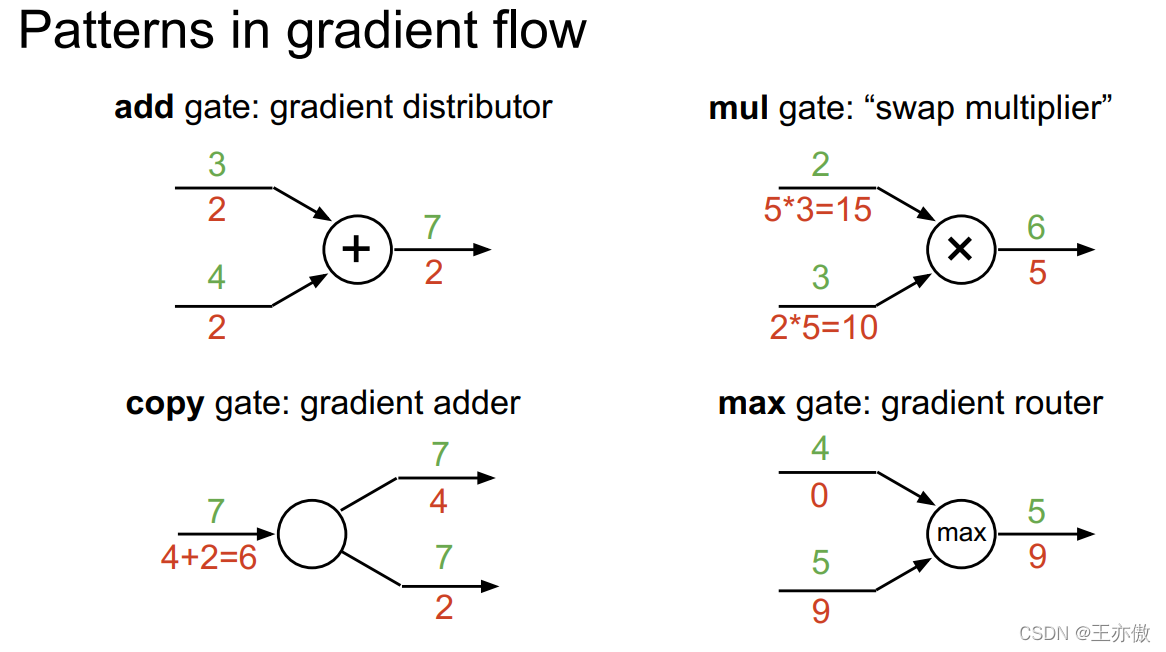
1、加法：加法分支的梯度就是上游梯度。
2、乘法：某一分支的梯度为上游梯度乘上另一分支的输入。
3、复制：每一分支的梯度相加的和。
4、max：梯度向输入较大的方向流动，较小输入的梯度为0。

代码

??对于一个神经网络，它是由许多一个个相似的block堆叠而成。而对于Fully-Connected网络，其block是由仿射变换（$Z=XW$），激活函数（这里是$ReLU$）组成。但是需要注意的是，由于需要输出分数，并利用分数得到其损失函数。所以在最后一层，我们不需要激活函数，而将激活函数改为损失函数即可。综上所诉，我们的网络结构为：输入($32?32?32+1=3073$)→通过仿射变换和激活函数ReLU→隐层激活→仿射变换和损失函数→输出。
??首先我们需要编写仿射变换的前向和后向函数，ReLU的前祥和后向函数，以及激活函数的输出和梯度。代码如下：

import numpy as np

def forward_affine(X,W,b):
    num_X = X.shape[0]
    X_reshape = X.reshape((num_X,-1))
    out = X_reshape @ W + b
    cache = (X,W,b)
    return out,cache

def backward_affine(ups_grad,cache):
    X,W,b = cache
    num_X = X.shape[0]
    X_reshape = X.reshape((num_X,-1))
    db = np.sum(ups_grad,axis=0)
    dW = X_reshape.T @ ups_grad
    dX = ups_grad @ W.T
    dX = dX.reshape(X.shape)
    return dX,dW,db

def forward_relu(x):
    out = (x > 0) * x
    cache = x
    return out,cache

def backward_relu(ups_grad,cache):
    x = cache
    dx = ups_grad * (x > 0)
    return dx

def svm_loss(x,y):
    
    num_x = x.shape[0]
    x_correct = x[range(num_x),y]
    delta_x = x - x_correct.reshape((num_x,1)) + 1
    Indicter = (delta_x > 0)
    Indicter[range(num_x),y] = 0
    loss_matrix = delta_x * Indicter
    loss = np.sum(loss_matrix) / num_x
    
    y_matrix = np.zeros(x.shape)
    y_matrix[range(num_x),y] = 1
    first_term = np.ones(x.shape)
    first_term = first_term * Indicter
    num_not_zero = np.sum(Indicter,axis=1).reshape((num_x,1))
    second_term = num_not_zero * y_matrix
    grad = first_term - second_term
    grad /= num_x
    
    return loss,grad

def softmax_loss(x,y):
    num_x,d = x.shape
    exp_x = np.exp(x)
    
    prob = exp_x / np.sum(exp_x,axis=1).reshape((num_x,1))
    log_prob = - np.log(prob)
    loss = np.sum(log_prob[range(num_x),y])/num_x
    
    y_matrix = np.zeros(x.shape)
    y_matrix[range(num_x),y] = 1
    grad = exp_x / np.sum(exp_x,axis=1).reshape((num_x,1))
    grad = - y_matrix + grad
    grad = grad / num_x
    return loss,grad

这里每个前向传播函数的输出cache保存了前向传播过程中所用到的值，而这个值在前向传播中保存下来并传给后向传播函数作为输入。ups_grad表示较高的层所传来的上游梯度，它和局部梯度相乘得到输出的梯度，并作为向前传播，作为前面的层的上游梯度。这里的svm_loss和softmax_loss都是损失函数，他们都输出函数的计算值和函数的梯度。关于svm_loss和softmax_loss在SVM损失函数和softmax损失函数做了更加详尽的叙述。
??接着我们将这些函数组成一个block（仿射变换＋ReLU）:

import forward_backward as fb

def forward_affine_relu(X,W,b):
    out_affine,cache_affine = fb.forward_affine(X,W,b)
    out,cache_relu = fb.forward_relu(out_affine)
    cache = (cache_affine,cache_relu)
    return out,cache

def backward_affine_relu(ups_grad,cache):
    cache_affine,cache_relu = cache
    da = fb.backward_relu(ups_grad,cache_relu)
    dX,dW,db = fb.backward_affine(da,cache_affine)
    return dX,dW,db

这里需要注意的是对于backward_affine_relu中da为ReLU函数的梯度，也就是fb.backward_affine的上游梯度。
??最后我们将以上这些代码整合到一起，组成一个两层的Fully-Connected网络。

import numpy as np
import layer_utils as lu
import forward_backward as fb

class TwoLayerNet():
    def __init__(self,input_size=32*32*3,hidden_size=100,num_class=10,ini_scale
                 =1e-3,reg=0):
        self.params = {}
        self.reg = reg
        
        self.params['W1'] = np.random.randn(input_size,hidden_size)*ini_scale
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = np.random.randn(hidden_size,num_class) * ini_scale
        self.params['b2'] = np.zeros(num_class)
        
    def loss(self,X,y=None):
        
        W1 = self.params['W1']
        b1 = self.params['b1']
        W2 = self.params['W2']
        b2 = self.params['b2']
        
        out1,cache1 = lu.forward_affine_relu(X,W1,b1)
        score,cache2 = fb.forward_affine(out1,W2,b2)
        
        if y is None:
            return score
        grad = {}
        loss,grad_softmax = fb.softmax_loss(score,y)
        loss = loss + 0.5 * self.reg * np.sum(W1*W1) + 0.5 * self.reg * np.sum(W2*W2)
        
        grad_L = 1
        grad_softmax = grad_softmax * grad_L
        dout1,dW2,db2 = fb.backward_affine(grad_softmax,cache2)
        
        dX,dW1,db1 = lu.backward_affine_relu(dout1,cache1)
        dW1 = dW1 + self.reg * W1
        dW2 = dW2 + self.reg * W2
        
        grad['W1'] = dW1
        grad['W2'] = dW2
        grad['b1'] = db1
        grad['b2'] = db2
        
        return loss,grad
    
    def train(self,X,y,X_val,y_val,lr=1e-3,lr_decay = 0.95,num_epoches=10,batch_size=100,print_every=None):
        num_tr = X.shape[0]
        iters_number = (num_tr // batch_size) * num_epoches
        tr_loss_history = []
        for i in range(iters_number):
            mask = np.random.choice(num_tr,batch_size,replace=False)
            X_batch = X[mask]
            y_batch = y[mask]
            loss,grad = self.loss(X_batch,y_batch)
            loss_val,_ = self.loss(X_val,y_val)
            tr_loss_history.append(loss)
            self.params['W1'] -= lr * grad['W1']
            self.params['W2'] -= lr * grad['W2']
            self.params['b1'] -= lr * grad['b1']
            self.params['b2'] -= lr * grad['b2']
            if (i+1) % num_tr == 0:
                lr = lr * lr_decay
            if print_every is not None and (i+1) % print_every ==0 :
                print('(Iteration %d / %d) loss:%f' % (i+1,iters_number,loss))
           
            if print_every is not None and ((i+1)*batch_size) % num_tr == 0:
                y_pre_on_train = self.predict(X)
                y_pre_on_val = self.predict(X_val)
                acc_tr = np.sum(y_pre_on_train == y) / y.shape[0]
                acc_val = np.sum(y_pre_on_val == y_val) / y_val.shape[0]
                print('(Epoch %d / %d) train acc:%f;val_acc:%f' % ((i+1)*batch_size/num_tr,num_epoches,\
                                                                   acc_tr,acc_val))
    def predict(self,X):
        out1,cache1 = lu.forward_affine_relu(X,self.params['W1'],self.params['b1'])
        score,cache2 = fb.forward_affine(out1,self.params['W2'],self.params['b2'])
        y = np.argmax(score,axis=1)
        return y

这里的loss计算了每一步的梯度损失函数以及每一步的梯度，其梯度存在grad字典中。这里的train方法则利用随机梯度下降对网络进行训练，这里X和y为训练集和训练集的标签。而train则接受验证集X_val,y_val来计算迭代中的验证误差。由于在训练过程不断收敛，为了防止过收敛，我们可以设定一个小于1的衰减系数使得学习率在训练过程中不断减小，lr_decay表示学习率lr在训练过程中的衰减系数。
??关于num_epoches的解释，我们则需要搞清楚和为epoch。一个epoch表示在训练过程中迭代使用到的样本数和训练集样本数相等的周期。batch的大小则是随机梯度下降中一次迭代所使用的样本数。很显然，batch的大小，epoch的个数和迭代次数具有以下关系：
$$训练集的大小\times epoch的个数=迭代次数\times batch的大小$$
所以代码中迭代次数为iters_number = (num_tr // batch_size) * num_epoches。print_every表示迭代每隔几次打印损失，同时如果不为None则在每隔epoch打印训练集和验证集的准确率。
??predict方法则对新样本进行预测：

model = fc.TwoLayerNet()
model.train(X_tr,y_tr,X_val,y_val,print_every=100,num_epoches=15)

y_pre_on_test = model.predict(X_test)
print('acc_test:%f' % (np.sum(y_pre_on_test==y_test)/y_test.shape[0]))

得到：

The shape of training data is (40000, 32, 32, 3)
The shape of training label is (40000,)
The shape of validation set is (10000, 32, 32, 3)
The shape of validation lbbel is (10000,)
(Iteration 100 / 6000) loss:1.734782
(Iteration 200 / 6000) loss:1.798886
(Iteration 300 / 6000) loss:1.699087
(Iteration 400 / 6000) loss:1.500601
(Epoch 1 / 15) train acc:0.448875;val_acc:0.428800
(Iteration 500 / 6000) loss:1.575010
(Iteration 600 / 6000) loss:1.399249
(Iteration 700 / 6000) loss:1.382878
(Iteration 800 / 6000) loss:1.392504
(Epoch 2 / 15) train acc:0.468775;val_acc:0.445000
(Iteration 900 / 6000) loss:1.316797
(Iteration 1000 / 6000) loss:1.402353
(Iteration 1100 / 6000) loss:1.577127
(Iteration 1200 / 6000) loss:1.425478
(Epoch 3 / 15) train acc:0.507625;val_acc:0.469500
(Iteration 1300 / 6000) loss:1.260583
(Iteration 1400 / 6000) loss:1.320702
(Iteration 1500 / 6000) loss:1.309578
(Iteration 1600 / 6000) loss:1.465867
(Epoch 4 / 15) train acc:0.515400;val_acc:0.460000
(Iteration 1700 / 6000) loss:1.421130
(Iteration 1800 / 6000) loss:1.523372
(Iteration 1900 / 6000) loss:1.461384
(Iteration 2000 / 6000) loss:1.336744
(Epoch 5 / 15) train acc:0.533300;val_acc:0.469700
(Iteration 2100 / 6000) loss:1.343402
(Iteration 2200 / 6000) loss:1.402489
(Iteration 2300 / 6000) loss:1.334701
(Iteration 2400 / 6000) loss:1.438204
(Epoch 6 / 15) train acc:0.547600;val_acc:0.475700
(Iteration 2500 / 6000) loss:1.872564
(Iteration 2600 / 6000) loss:1.422237
(Iteration 2700 / 6000) loss:1.402053
(Iteration 2800 / 6000) loss:1.378892
(Epoch 7 / 15) train acc:0.545350;val_acc:0.465900
(Iteration 2900 / 6000) loss:1.282605
(Iteration 3000 / 6000) loss:1.170192
(Iteration 3100 / 6000) loss:1.224985
(Iteration 3200 / 6000) loss:1.193151
(Epoch 8 / 15) train acc:0.567350;val_acc:0.473300
(Iteration 3300 / 6000) loss:1.364777
(Iteration 3400 / 6000) loss:1.389250
(Iteration 3500 / 6000) loss:1.063959
(Iteration 3600 / 6000) loss:1.028074
(Epoch 9 / 15) train acc:0.561425;val_acc:0.464100
(Iteration 3700 / 6000) loss:1.197675
(Iteration 3800 / 6000) loss:1.151499
(Iteration 3900 / 6000) loss:1.378195
(Iteration 4000 / 6000) loss:1.298935
(Epoch 10 / 15) train acc:0.571675;val_acc:0.463600
(Iteration 4100 / 6000) loss:1.029373
(Iteration 4200 / 6000) loss:0.969321
(Iteration 4300 / 6000) loss:1.474264
(Iteration 4400 / 6000) loss:1.009141
(Epoch 11 / 15) train acc:0.604525;val_acc:0.493400
(Iteration 4500 / 6000) loss:1.017987
(Iteration 4600 / 6000) loss:1.000179
(Iteration 4700 / 6000) loss:1.151042
(Iteration 4800 / 6000) loss:1.307574
(Epoch 12 / 15) train acc:0.585475;val_acc:0.478700
(Iteration 4900 / 6000) loss:0.982761
(Iteration 5000 / 6000) loss:1.227296
(Iteration 5100 / 6000) loss:1.388272
(Iteration 5200 / 6000) loss:1.084682
(Epoch 13 / 15) train acc:0.607800;val_acc:0.481600
(Iteration 5300 / 6000) loss:1.282598
(Iteration 5400 / 6000) loss:1.135463
(Iteration 5500 / 6000) loss:1.223011
(Iteration 5600 / 6000) loss:1.215135
(Epoch 14 / 15) train acc:0.611025;val_acc:0.484300
(Iteration 5700 / 6000) loss:1.184923
(Iteration 5800 / 6000) loss:1.136357
(Iteration 5900 / 6000) loss:1.036550
(Iteration 6000 / 6000) loss:1.093990
(Epoch 15 / 15) train acc:0.621400;val_acc:0.493800
acc_test:0.482000

由于我们every_print=100,所以我们这里每100次迭代打印一次损失，且每一次epoch打印一次训练集上的准确率和验证集上的准确率。
??这里有几点值得注意：1 随着迭代次数的增加，损失总体来说越来越小：我们这里每次迭代是从训练集中随机选取数据进行一次迭代，但是每次选取数据具有重复，所以每次选取数据在一定程度上具有相同分布。所以损失具有波动，但是总体是下降的。2 由于我们的模型是在训练集上训练，所以模型是要去拟合训练上的数据，所以每个epoch的训练准确度总体在上升。而验证集上的上升幅度并没有训练集上的大。3 我们这里的准确率并不高，一方面是由于我们并没有使用正则化（正则化项为0），另外两个重要的方面是：网络的层数过少和模型本身的局限性。对于图片分类等视觉任务，现在最好的方法是卷积神经网络（CNN）。