在看北邮鲁鹏老师的三维重建的课程过程中,去官网找到有三个作业。现将三个作业里面的第一个作业相机标定完成。总体来说,可以分为三个部分,即图像坐标点和世界坐标点的获取;映射矩阵的生成,相机内外参的求解三个部分。现总结如下:
图像坐标点的获取
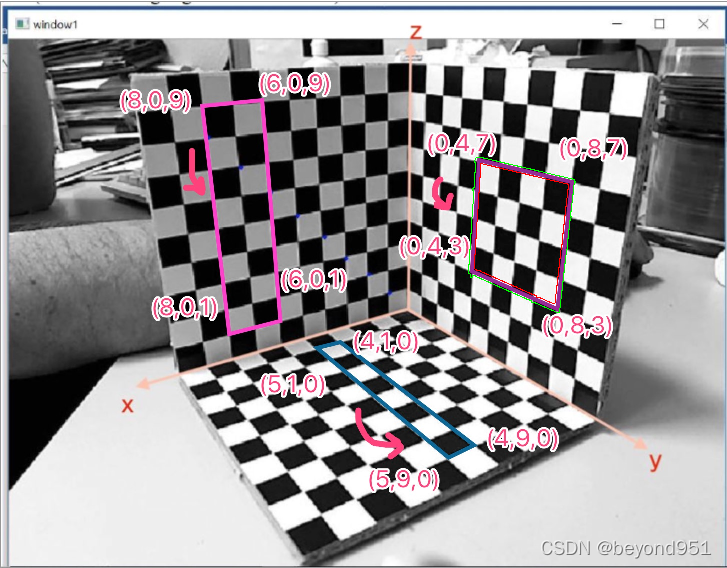
上鲁鹏老师作业里边的标定图,如下图所示:
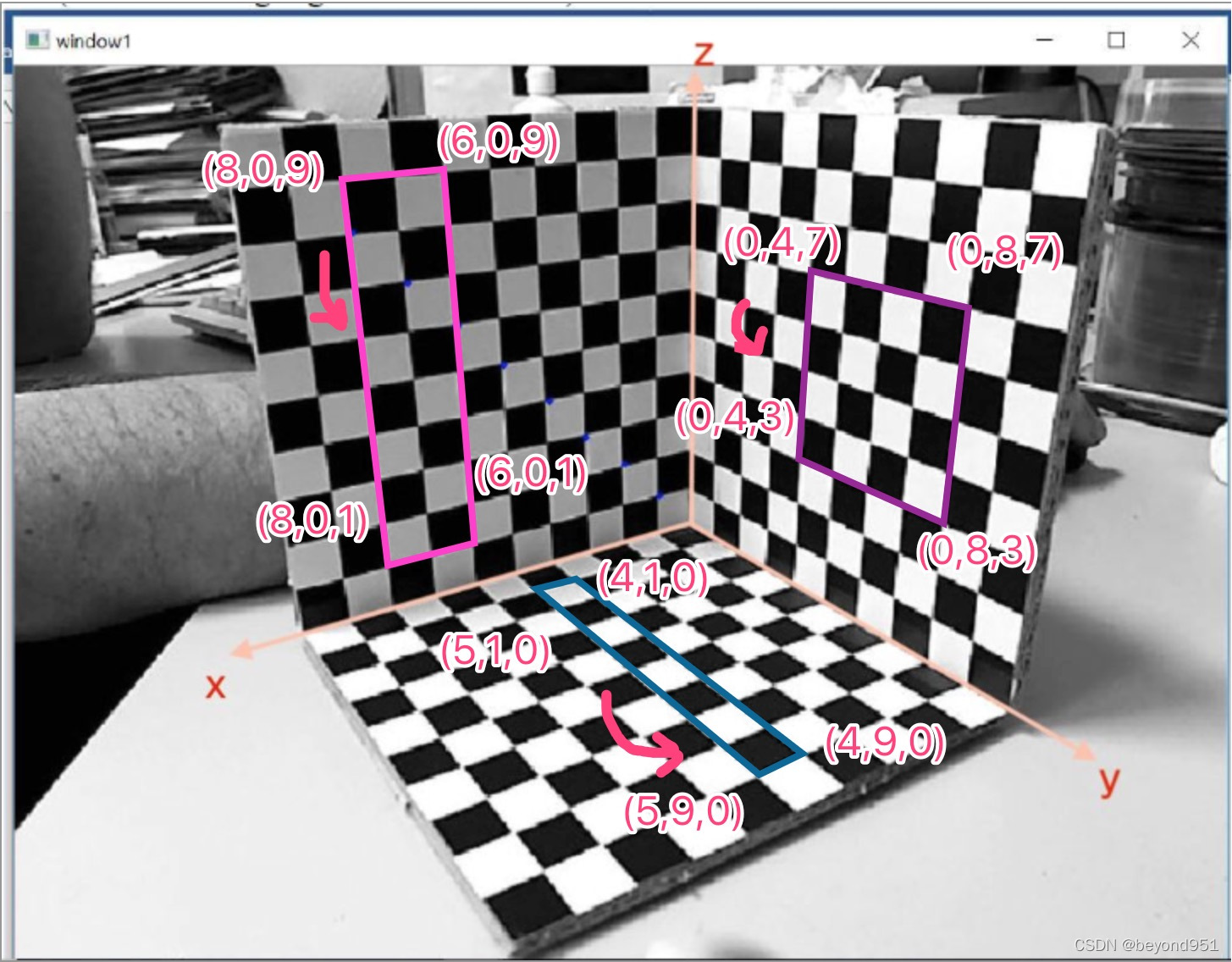
?通过该图可以看到世界坐标系建立在立体标版的原点,一个方形格子代表单位1,三个互相垂直的平面上各取了四个点,并用框标明了。因此,我们第一步就是要获得上述12个点的图像坐标。
在这里,我用halcon对图像进行处理,获取到框内外的边缘,并对角点像素坐标估算,求内外角点平均值得到图像坐标点。(这里本来想直接求角点的,最后估算了一下)
有更好的方法可以交流。
得到对应的点的关系如下:
?(0,8,7)->(363.5,1143) (0,4,7)->(320,958) ?(0,8,3)->(616,1112) ?(0,4,3)->(542,943)
?(8,0,9)->(212,404) ? ?(6,0,9)->(201,523) ?(8,0,1)->(667,459) ?(6,0,1)->(642,559)
?(4,1,0)->(684,679) ? ?(5,1,0)->(695,635) ?(5,9,0)->(913,896) ?(4,9,0)->(889,946)
read_image (Jietu20200301091513, 'E:/文件文档/鲁鹏-三维重建资料/Total3DExercises-main/MVGlab01_camera-calibration-master/images/Jietu20200301-091513.jpg')
get_image_size (Jietu20200301091513, Width, Height)
dev_clear_window ()
dev_close_window ()
dev_open_window (0, 0, Width/2, Height/2, 'black', WindowHandle)
dev_display (Jietu20200301091513)
rgb1_to_gray (Jietu20200301091513, GrayImage)
*寻找第一个和第二个矩形区域
threshold (GrayImage, Region, 75, 90)
connection (Region, ConnectedRegions)
fill_up (ConnectedRegions, RegionFillUp)
select_shape (RegionFillUp, SelectedRegions1, ['rectangularity','area'], 'and', [0.7,17500], [1,50000])
*寻找第三个矩形区域
dev_clear_window ()
dev_display (Jietu20200301091513)
threshold (GrayImage, Region1, 128, 140)
connection (Region1, ConnectedRegions1)
fill_up (ConnectedRegions1, RegionFillUp1)
select_shape (RegionFillUp1, SelectedRegions2, ['rectangularity','area'], 'and', [0.7,40000], [1,80000])
*将上述三个区域合并
concat_obj (SelectedRegions1, SelectedRegions2, ObjectsConcat)
count_obj (ObjectsConcat, Number)
dev_display (Jietu20200301091513)
dev_display (ObjectsConcat)
stop ()
*分别对三个区域进行形态学处理,并获得矩形边角的角点图像坐标
for Index := 1 to Number by 1
select_obj (ObjectsConcat, ObjectSelected, Index)
*最大的框
dilation_rectangle1 (ObjectSelected, RegionDilation, 31, 31)
*将该区域像素全部置为255
paint_region (RegionDilation, GrayImage, ImageResult, 255, 'fill')
*膨胀操作,腐蚀操作,做差裁剪ROI
dilation_rectangle1 (ObjectSelected, RegionDilation1, 5, 5)
erosion_rectangle1 (RegionDilation1, RegionErosion, 21, 21)
difference (RegionDilation1, RegionErosion, RegionDifference)
paint_region (RegionDifference, ImageResult, ImageResult2, 0, 'fill')
reduce_domain (ImageResult2, RegionDilation, ImageReduced)
invert_image (ImageReduced, ImageInvert)
edges_sub_pix (ImageInvert, Edges1, 'canny', 1, 20, 40)
select_contours_xld (Edges1, SelectedContours, 'contour_length', 100, 30000, 100, 30000)
dev_display (Jietu20200301091513)
dev_display (SelectedContours)
endfor?提取出边框的内外轮廓,根据内外轮廓估计角点位置。
生成图像坐标点到世界坐标点的映射矩阵
首先通过鲁鹏老师的课件进行说明:

?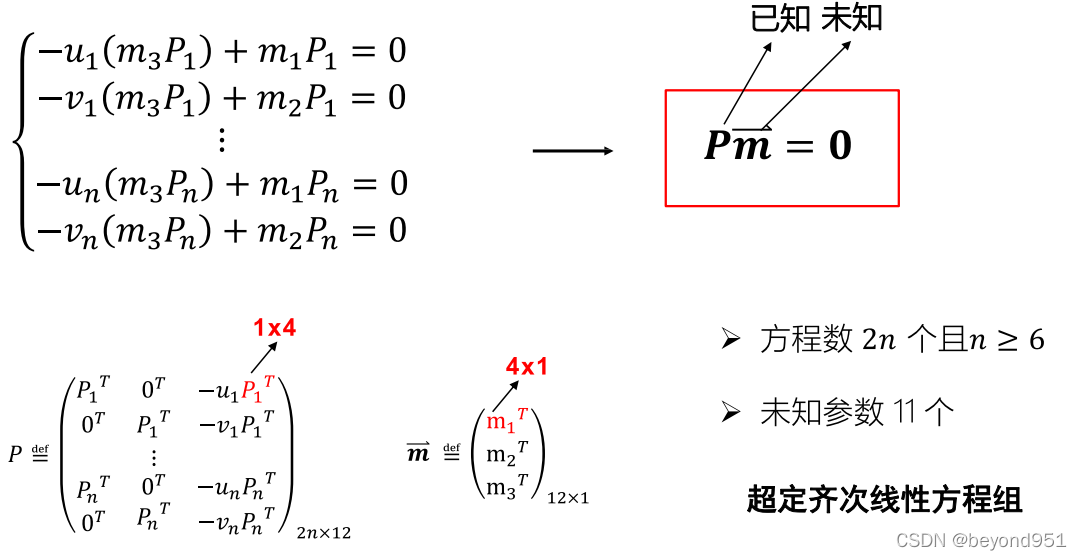
?也就是,基于图像和世界坐标点对应的关系,构建P矩阵,这里我用C++ OPENCV进行构建:
#include "stdafx.h"
#include <stdio.h>
#include <cmath>
#include<io.h>
#include <fstream>
#include <iostream>
#include <direct.h>
#include <opencv2/opencv.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <map>
#include <algorithm>
using namespace std;
using namespace cv;
int main()
{
?? ?//读取标定图像文件
?? ?Mat src = imread(".\\images\\Jietu20200301-091513.jpg",4);
?? ?//找到图像点对应标版坐标系世界点的坐标关系
?? ?//根据imagewatch可以看到相关的关系
?? ?//先找到图像中对应四边形的角点
?? ?//(0,8,7)->(363.5,1143) (0,4,7)->(320,958) ?(0,8,3)->(616,1112) ?(0,4,3)->(542,943)
?? ?//(8,0,9)->(212,404) ? ?(6,0,9)->(201,523) ?(8,0,1)->(667,459) ?(6,0,1)->(642,559)
?? ?//(4,1,0)->(684,679) ? ?(5,1,0)->(695,635) ?(5,9,0)->(913,896) ?(4,9,0)->(889,946)
?? ?//根据上面的点开始构建矩阵关系
?? ?//声明两个动态数组用来存储点集
?? ?vector<Point3d> vec_worldpoints;
?? ?vector<Point2d> vec_picpoints;
?? ?vec_worldpoints.push_back(Point3f(0, 8, 7));
?? ?vec_worldpoints.push_back(Point3f(0, 4, 7));
?? ?vec_worldpoints.push_back(Point3f(0, 8, 3));
?? ?vec_worldpoints.push_back(Point3f(0, 4, 3));
?? ?vec_picpoints.push_back(Point2f(363.5, 1143));
?? ?vec_picpoints.push_back(Point2f(320, 958));
?? ?vec_picpoints.push_back(Point2f(616, 1112));
?? ?vec_picpoints.push_back(Point2f(542, 943));
?? ?vec_worldpoints.push_back(Point3f(8, 0, 9));
?? ?vec_worldpoints.push_back(Point3f(6, 0, 9));
?? ?vec_worldpoints.push_back(Point3f(8, 0, 1));
?? ?vec_worldpoints.push_back(Point3f(6, 0, 1));
?? ?vec_picpoints.push_back(Point2f(212, 404));
?? ?vec_picpoints.push_back(Point2f(201, 523));
?? ?vec_picpoints.push_back(Point2f(667, 459));
?? ?vec_picpoints.push_back(Point2f(642, 559));
?? ?vec_worldpoints.push_back(Point3f(4, 1, 0));
?? ?vec_worldpoints.push_back(Point3f(5, 1, 0));
?? ?vec_worldpoints.push_back(Point3f(5, 9, 0));
?? ?vec_worldpoints.push_back(Point3f(4, 9, 0));
?? ?vec_picpoints.push_back(Point2f(684, 679));
?? ?vec_picpoints.push_back(Point2f(695, 635));
?? ?vec_picpoints.push_back(Point2f(913, 896));
?? ?vec_picpoints.push_back(Point2f(889, 946));
?? ?//将上述点用来构建矩阵
?? ?Mat P = (Mat_<double>(24, 12));
?? ?for (int i = 0; i < 12; i++)
?? ?{
?? ??? ?//第一行(奇数行)赋值
?? ??? ?P.at<double>(2 * i, 0) = vec_worldpoints[i].x;
?? ??? ?P.at<double>(2 * i, 1) = vec_worldpoints[i].y;
?? ??? ?P.at<double>(2 * i, 2) = vec_worldpoints[i].z;
?? ??? ?P.at<double>(2 * i, 3) = 1;
?? ??? ?P.at<double>(2 * i, 4) = 0;
?? ??? ?P.at<double>(2 * i, 5) = 0;
?? ??? ?P.at<double>(2 * i, 6) = 0;
?? ??? ?P.at<double>(2 * i, 7) = 0;
?? ??? ?P.at<double>(2 * i, 8) = -(vec_picpoints[i].x)*(vec_worldpoints[i].x);
?? ??? ?P.at<double>(2 * i, 9) = -(vec_picpoints[i].x)*(vec_worldpoints[i].y);
?? ??? ?P.at<double>(2 * i, 10) = -(vec_picpoints[i].x)*(vec_worldpoints[i].z);
?? ??? ?P.at<double>(2 * i, 11) = -vec_picpoints[i].x;
?? ??? ?//第二行(偶数行)赋值
?? ??? ?P.at<double>(2 * i + 1, 0) = 0;
?? ??? ?P.at<double>(2 * i + 1, 1) = 0;
?? ??? ?P.at<double>(2 * i + 1, 2) = 0;
?? ??? ?P.at<double>(2 * i + 1, 3) = 0;
?? ??? ?P.at<double>(2 * i + 1, 4) = vec_worldpoints[i].x;
?? ??? ?P.at<double>(2 * i + 1, 5) = vec_worldpoints[i].y;
?? ??? ?P.at<double>(2 * i + 1, 6) = vec_worldpoints[i].z;
?? ??? ?P.at<double>(2 * i + 1, 7) = 1;
?? ??? ?P.at<double>(2 * i + 1, 8) = -(vec_picpoints[i].y)*(vec_worldpoints[i].x);
?? ??? ?P.at<double>(2 * i + 1, 9) = -(vec_picpoints[i].y)*(vec_worldpoints[i].y);
?? ??? ?P.at<double>(2 * i + 1, 10) = -(vec_picpoints[i].y)*(vec_worldpoints[i].z);
?? ??? ?P.at<double>(2 * i + 1, 11) = -vec_picpoints[i].y;
?? ?}
?? ?return 0;
}这里推荐VS的插件imagewatch,可以直接将opencv里边的mat类型变量可视化,构建后的矩阵如下图所示:
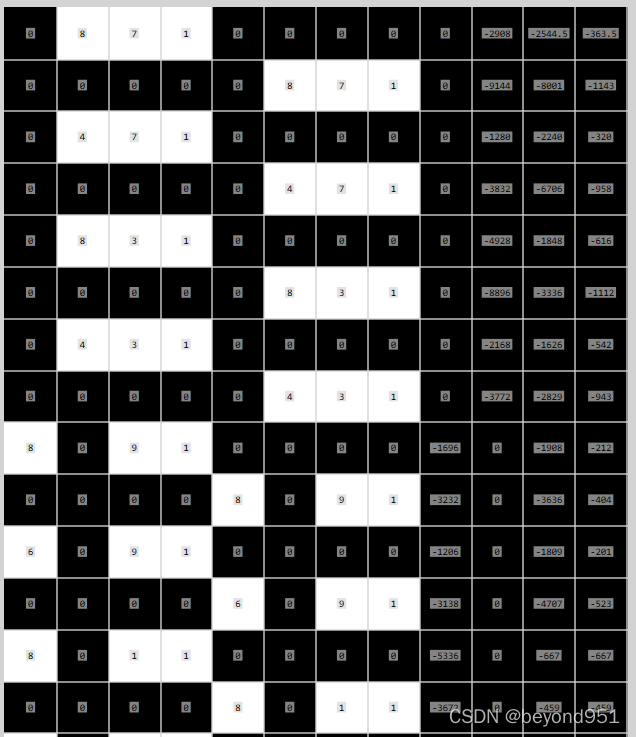
这里本来是一个24行的矩阵,只截取出部分行。接着就是对该矩阵进行奇异值分解?
//对矩阵P进行奇异值分解,并分别求右矩阵的转置和逆
//因为右矩阵为正交矩阵,所以他的逆和装置相等
Mat W, U, Vt;
SVD::compute(P, W, U, Vt, 4);
Mat Vtt = Vt.t();
Mat Vtinv = Vt.inv();
//根据奇异值分解得到的右矩阵,得到透视投影矩阵M
//p=MP ?p为图像坐标点,P为世界坐标点
//下面就是矩阵的赋值
Mat M(Mat_<double>(3, 4));
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 4; j++)
{
switch (i)
{
case 0:
M.at<double>(i, j) = Vtt.at<double>(j, 11);
break;
case 1:
M.at<double>(i, j) = Vtt.at<double>(j + 4, 11);
break;
case 2:
M.at<double>(i, j) = Vtt.at<double>(j + 8, 11);
break;
default:
break;
}
}
}
//来个点进行测试,将上述一个世界坐标系点齐次坐标形式(0,8,7,1)与M相乘
//得到放缩系数
//检验出来图像坐标为(363.13,1142.6)与对应的图像坐标(363.5,1143)误差在一个像素以内
Mat picPoint, worldPoint, uvPoint;
worldPoint = (Mat_<double>(4, 1) << 0.0, 8.0, 7.0, 1.0);
picPoint = M*worldPoint;
double scalFactor = 1 / picPoint.at<double>(2, 0);
uvPoint = scalFactor*picPoint;分解得到右向量的最后一个列向量,即最小奇异值对应的列向量,将该向量转为3*4的矩阵形式,其矩阵如下图所示:(如果对上面代码有问题,想去看看鲁鹏老师课程,对照课件就明了了)
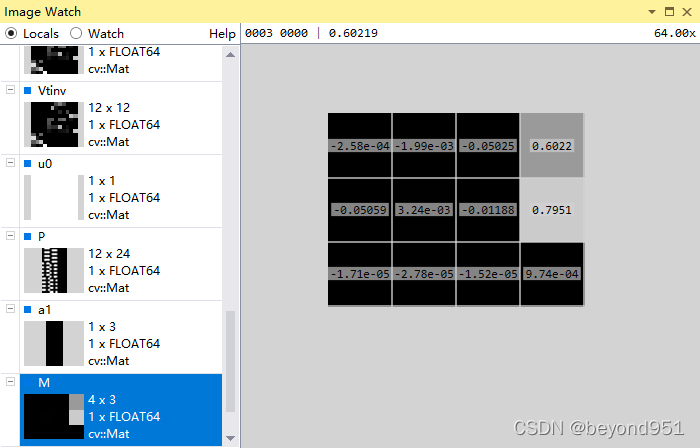
?到这里为校验下M矩阵的精度,对世界坐标点(0,8,7,1)进行重投影,即p=MP,将世界坐标点代入投影矩阵,得到图像坐标uo,v0,与原值图像坐标(363.5,1143)进行对比。
下图为将上述一个世界坐标系点齐次坐标形式(0,8,7,1)与M相乘,经过放缩得到的u0,v0
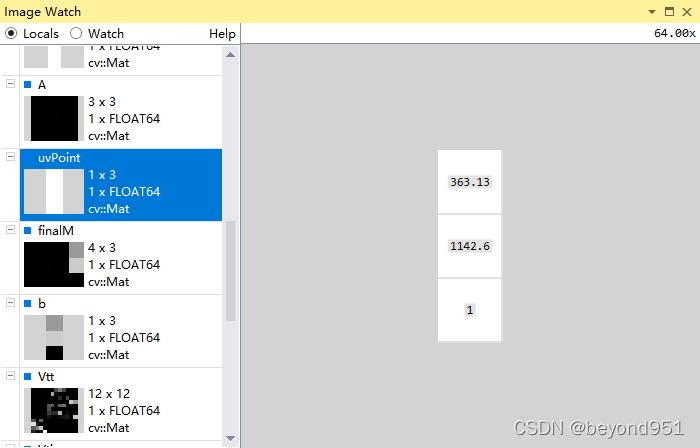
?检验出来图像坐标为(363.13,1142.6)与对应的图像坐标(363.5,1143)误差在一个像素以内。
相机内外参数的求取
那么接下来就是根据M矩阵求解相机的内外参数,还是那句话,对过程有疑问,去复习视频和课件,只要脑海中有那个过程,代码很好理解。
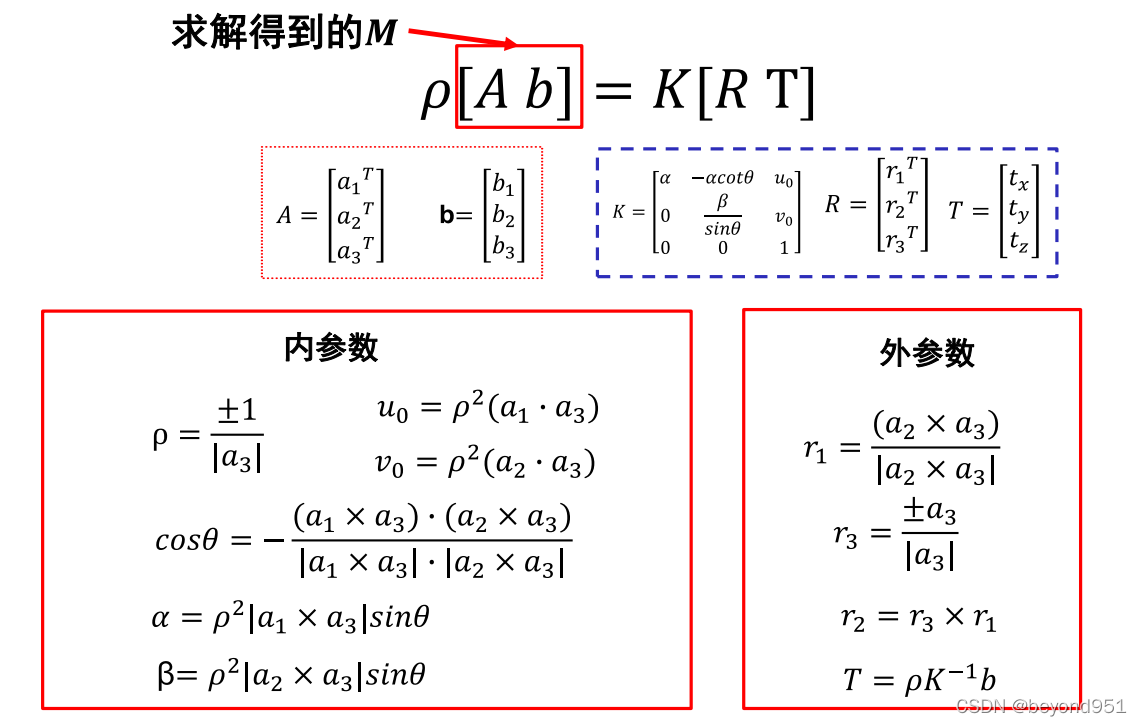
?所有参数的求解,都是基于上面图片的这些公式。
Mat finalM = M;
//我们知道p=finalM*P,其中p为图像坐标系的齐次坐标,P为世界坐标系的齐次坐标
//finalM为确定了放缩系数以后的透视投影矩阵
//p=finalM*P=K*[R T]*P
//K*[R T]=finalM=[A b]
//同时我们知道R T外参矩阵对应旋转平移,旋转为3*3,平移为3*1
//因此我们得到矩阵A为finalM的左边三列,矩阵b为finalM的最右一列
//先分离出A b矩阵
Mat A = (Mat_<double>(3, 3));
Mat b = (Mat_<double>(3, 1));
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
A.at<double>(i, j) = finalM.at<double>(i, j);
}
}
for (size_t i = 0; i < 3; i++)
{
b.at<double>(i, 0) = finalM.at<double>(i, 3);
}
//求A的转置
Mat At = A.t();
//分解出a1,a2,a3,之前先转置
//声明三个列向量
Mat a1 = (Mat_<double>(3, 1));
Mat a2 = (Mat_<double>(3, 1));
Mat a3 = (Mat_<double>(3, 1));
for (int i = 0; i < 3; i++)
{
a1.at<double>(i, 0) = At.at<double>(i, 0);
a2.at<double>(i, 0) = At.at<double>(i, 1);
a3.at<double>(i, 0) = At.at<double>(i, 2);
}
//先求放缩系数
double a31 = a3.at<double>(0, 0);
double a32 = a3.at<double>(1, 0);
double a33 = a3.at<double>(2, 0);
double factor = 1.0 / sqrt(pow(a31, 2) + pow(a32, 2) + pow(a33, 2));
//开始求内参,先求中心点u0 和v0
Mat u0 = pow(factor, 2)* a1.t()*a3;
Mat v0 = pow(factor, 2)* a3.t()*a2;到这里,我们求得了相机内参的中心点,uo,v0(634.93,736.16)
中心点偏差好像有点大,但不算特别离谱,因为这里是默认理想透视模型,忽略了畸变。
//接着求内参theta角
?? ?//cos(theta)=-[(a1×a3)·(a2×a3)]/[|a1×a3|·|a2×a3|]
?? ?//先写一个向量叉乘的函数
?? ?//上面将a1,a2,a3向量,以矩阵形式表示的,这里用opencv的Vec3f表示
?? ?Vec3d A1, A2, A3;
?? ?for (int i = 0; i < 3; i++)
?? ?{
?? ??? ?A1[i] = At.at<double>(i, 0);
?? ??? ?A2[i] = At.at<double>(i, 1);
?? ??? ?A3[i] = At.at<double>(i, 2);
?? ?}
?? ?double factor1 = 1.0 / sqrt(pow(A3[0], 2) + pow(A3[1], 2) + pow(A3[2], 2));
?? ?double U0 = pow(factor1, 2)* A1.dot(A3);
?? ?double V0 = pow(factor1, 2)* A3.dot(A2);
?? ?//定义costheta
?? ?//自定义一个函数计算,两个向量叉乘的模
?? ?double costhea = -(A1.cross(A3)).dot(A2.cross(A3)) / (ModulusofCrossProduct(A1, A3)*ModulusofCrossProduct(A2, A3));
?? ?double sinthea = sqrt(1 - pow(costhea, 2));
?? ?//接着求解水平、垂直方向的焦距alpha、beta
?? ?double alpha = pow(factor1, 2)*ModulusofCrossProduct(A1, A3)*sinthea;
?? ?double beta = pow(factor1, 2)*ModulusofCrossProduct(A2, A3)*sinthea;
?? ?//至此,相机的内部参数求解完毕
?? ?//开始求解相机外参
?? ?//r1=(a2×a3)/|a2×a3| ?r3=±a3/|a3| ? r2=r1×r3
?? ?Vec3d r1 = A2.cross(A3) / ModulusofCrossProduct(A2, A3);
?? ?Vec3d r3 = A3 / sqrt(pow(A3[0], 2) + pow(A3[1], 2) + pow(A3[2], 2));
?? ?Vec3d r2 = r1.cross(r3);
?? ?Mat Rt = (Mat_<double>(3, 3));
?? ?//将向量赋值给Rt矩阵
?? ?for (int i = 0; i < 3; i++)
?? ?{
?? ??? ?Rt.at<double>(0, i) = r1[i];
?? ??? ?Rt.at<double>(1, i) = r2[i];
?? ??? ?Rt.at<double>(2, i) = r3[i];
?? ?}
?? ?Mat R = Rt.t();
?? ?//平移矩阵T=pK(-1)b ?这里p为放缩系数,K(-1)为相机内参矩阵的逆,b矩阵为M矩阵里面分解出来的
?? ?//首先根据求出来的内部参数,构建内参矩阵K
?? ?Mat K = (Mat_<double>(3, 3));
?? ?K.at<double>(0, 0) = alpha;
?? ?K.at<double>(0, 1) = -alpha*(costhea/sinthea);
?? ?K.at<double>(0, 2) = U0;
?? ?K.at<double>(1, 0) = 0;
?? ?K.at<double>(1, 1) = beta/sinthea;
?? ?K.at<double>(1, 2) = V0;
?? ?K.at<double>(2, 0) = 0;
?? ?K.at<double>(2, 1) = 0;
?? ?K.at<double>(2, 2) = 1;
?? ?//求解T矩阵
?? ?Mat T = (Mat_<double>(3,1));
?? ?T = factor1*K.inv()*b;
?? ?return 0;
}
double ModulusofCrossProduct(Vec3d v1, Vec3d v2)
{
?? ?//向量维度不一样,直接返回零值
?? ?if (v1.cols!=v2.cols&&v1.rows!=v2.rows)
?? ?{
?? ??? ?return 0;
?? ?}
?? ?//两个向量的叉乘是一个矩阵
?? ?Vec3d m = v1.cross(v2);
?? ?//返回矩阵的行列式
?? ?double temp = sqrt(pow(m[0], 2) + pow(m[1], 2) + pow(m[2], 2));
?? ?return temp;
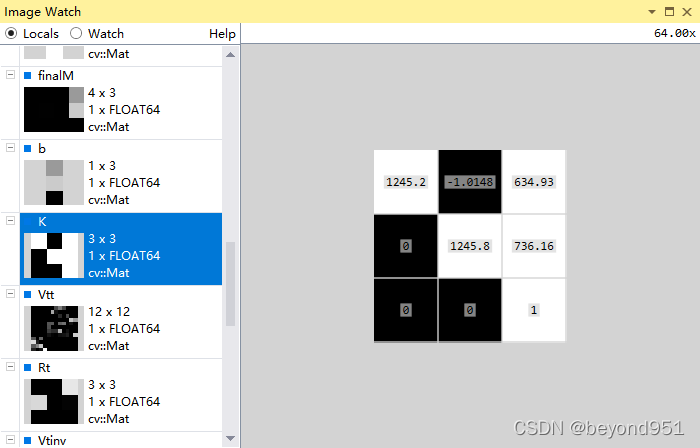
}最后得到相机的内参矩阵K、外参旋转矩阵R、外参平移矩阵T,其结果如图所示:
 ?
?
 ?
?
?至此,相机标定部分完成,接下来将实现单视图三维重建。