题目
transformer学习之Layer Normalization
简介
Normalization
字面翻译 —> 标准化
分类
N o r m a l i z a t i o n { ( 1 ) { B a t c h N o r m L a y e r N o r m 对 第 L 层 每 个 神 经 元 的 激 活 值 或 者 说 对 于 第 L + 1 层 网 络 神 经 元 的 输 入 值 进 行 N o r m a l i z a t i o n 操 作 ( 2 ) { W e i g h t N o r m 对 神 经 网 络 中 连 接 相 邻 隐 层 神 经 元 之 间 的 边 上 的 权 重 进 行 规 范 化 操 作 Normalization \begin{cases} (1)\begin{cases}BatchNorm\\LayerNorm \end{cases}对第L层每个神经元的激活值或者说对于第L+1层网络神经元的输入值进行Normalization操作\\ (2)\begin{cases}Weight Norm\end{cases} 对神经网络中连接相邻隐层神经元之间的边上的权重进行规范化操作 \end{cases}\\ Normalization????????(1){BatchNormLayerNorm?对第L层每个神经元的激活值或者说对于第L+1层网络神经元的输入值进行Normalization操作(2){WeightNorm?对神经网络中连接相邻隐层神经元之间的边上的权重进行规范化操作?
作用
对于第(1)类的Normalization,它的作用是将均值变为0,方差变为1,即使得数据分布在中间部分。
它的公式为
x
^
i
=
γ
i
?
x
i
?
μ
σ
i
+
β
i
\widehat x_i = \gamma_i·\frac{x_i-\mu}{\sigma_i}+\beta_i
x
i?=γi??σi?xi??μ?+βi?
μ
\mu
μ为均值,
σ
\sigma
σ为方差
γ i \gamma_i γi?和 β i \beta_i βi?是为了恢复原始某一层所学到的特征,使得模型的表达能力不因为规范化而下降
Batch Normalization
含义
利用网络训练一个 mini-batch 的数据来计算该神经元 x i x_i xi?的均值和方差,因而称为 Batch Normalization
公式
μ = 1 M ∑ i x i ???? σ = 1 M ∑ i ( x i ? μ ) 2 \mu=\frac{1}{M}\sum_ix_i\ \ \ \ \sigma=\sqrt{\frac{1}{M}\sum_i(x_i-\mu)^2} μ=M1?i∑?xi?????σ=M1?i∑?(xi??μ)2?
M M M为mini-batch大小
大致过程
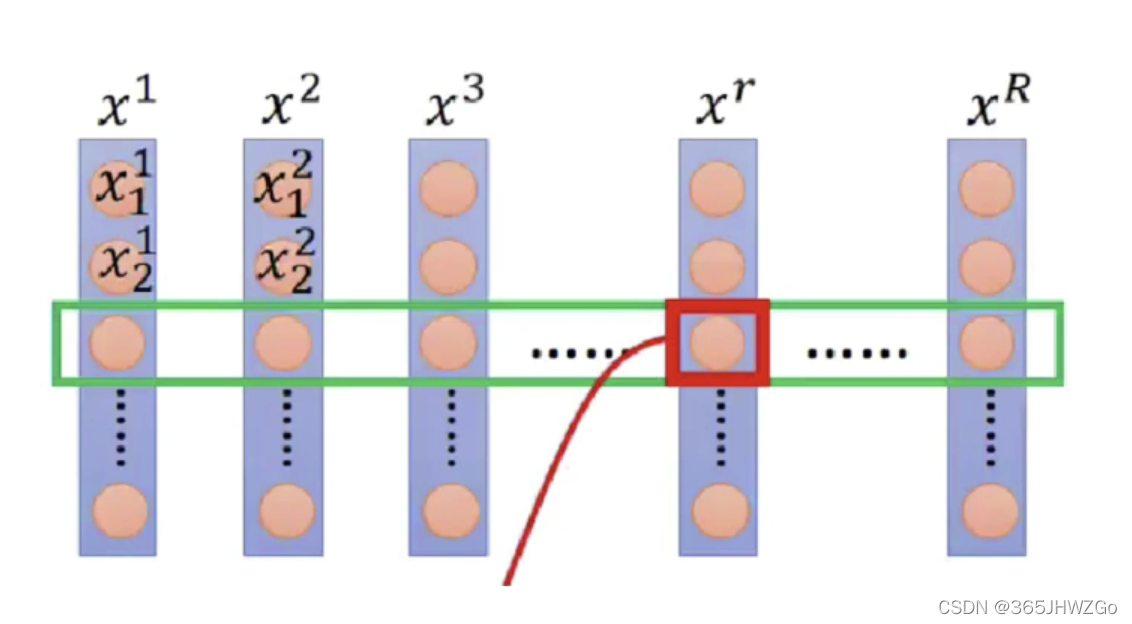
x 1 、 x 2 、 x 3 . . . x r . . . x R x^1、x^2、x^3...x^r...x^R x1、x2、x3...xr...xR为一个mini-batch内的句子
x 1 1 、 x 2 1 、 x 3 1 . . . x_1^1、x_2^1、x_3^1... x11?、x21?、x31?...为第 x 1 x^1 x1个句子中的单词
Batch Normalization是将每一个句子中同一位置的单词进行计算求解 x ^ i \widehat x_i x i?
缺点
从上述过程中也可以看出Batch Normalization的缺点有
- 每一个句子的单词长度应该尽量相同,否则在计算时就空缺

- 当mini-batch太小时,计算出来的均值会太大影响结果集
Layer Normalization
Layer Normalization就是针对 BN 的上述不足而提出的,它不再采用一个批次每个句子同一位置的单词作为采样点,而是变成采集一个句子中所有单词的数据。

公式
μ = 1 H ∑ i x i ???? σ = 1 H ∑ i ( x i ? μ ) 2 \mu=\frac{1}{H}\sum_ix_i\ \ \ \ \sigma=\sqrt{\frac{1}{H}\sum_i(x_i-\mu)^2} μ=H1?i∑?xi?????σ=H1?i∑?(xi??μ)2?
H H H为一个句子单词数
它是把一个句子中所有单词的输入,计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入
优点
- 起到缓解梯度消失/爆炸
- 加速训练、正则化的效果
- 适用于NLP中对于句子中单词数长短不一的情况