[人工智能]svm支持向量机

最大间隔与分类

当训练数据线性可分时，存在无数个超平面可以将两类数据正确分开。感知机利用误分类最小策略，可以求得无穷个解将超平面进行分离，线性可分支持向量机利用间隔最大化的求得分离超平面，此时的解为唯一解；另外，此时分类超平面所产生的的分类结果是最棒的，泛化性能最强。

线性模型

我们已经知道了函数间隔和几何间隔的表示，现在回到正题，我们需要最大化支持向量到分割超平面的距离，当然在最开始我们不知道哪些向量是支持向量。

我们的目的是最大化支持向量到分割超平面的几何间隔r，而不是最大化函数间隔g(x)，为什么呢？因为超平面方程的系数可以同比例增大或者减小，而不改变超平面本身。所以||w0||是不固定的，这就会影响函数间隔g(x)的大小。

所以我们需要最大化的是几何间隔r，这等价于我们固定||w0||，然后最大化函数间隔g(x)。但是实际上我们不会这么做，通常的处理方法是固定函数间隔g(x)的绝对值为1，然后最小化||w0||。也就是说我们把支持向量到分割超平面的函数间隔g(x)的绝对值设定为1，然后最小化||w0||。

在样本空间中寻找一个超平面, 将不同类别的样本分开


容忍性好, 鲁棒性高, 泛化能力最强，最大化决策边界的边缘

超平面方程: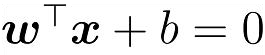

最大化间隔: 寻找参数w和b , 使得下述公式最大

对偶问题

KKT条件

大家已经知道slater条件已经确保了鞍点的存在，但是鞍点不一定就是最优解啊，所以KKT条件的作用便体现出来了。
KKT条件便是确保鞍点便是原函数最优解的充分条件，当然对于我们前面举得那个例子，当原问题是凸优化问题时，则KKT条件便是鞍点便是最优解的充要条件。

第一个约束条件表明：最优点x必须满足所有等式及不等式限制条件, 也就是说最优点必须是一个可行解, 这一点自然是毋庸置疑的；
第二个约束条件表明：在最优点x, ?f必须是?gi和?hj的线性組合;
第三个约束条件表明：拉格朗日乘子不等式的一些限制，对于不等式的拉格朗日乘子限制条件有方向性, 所以每一个α都必须大于或等于零, 而等式限制条件没有方向性，只是β不等于0。

总结

• 对偶问题将原始问题中的约束转为了对偶问题的等式约束，我们将目标函数和约束条件融入了一个新的函数，即拉格朗日函数，通过这个函数来寻找最优点。
• 可以很自然的引用核函数，从而推广至非线性分类问题。拉格朗日函数里面有内积，而核函数也是通过内积来进行映射的。
• 改变的问题的复杂度，由求特征向量w转化为求比例系数α,在原始问题下，求解的复杂度与样本的维度有关，在对偶问题下，只与样本的数量有关。

核函数

核函数不显式地构造核映射, 而是设计核函数
SVM原本是用来解决二分类的分类模型
它和感知机不同的一点是它取到的分类器是在特征空间上的最大间隔的分类器
而为了解决非线性的分类问题 SVM使用核技巧 所以在SVM中核函数的作用是解决了SVM无法处理非线性可分的问题

核函数本质

1. 在实际数据上经常遇到线性不可分的情况 而解决方法是将特征映射到更高维的空间去
2. 凡是遇到线性不可分的情况 一律映射到高维度空间 会出现维度爆炸的情况
3. 核函数虽然也是将特征进行从低维到高维的转化 但是是在低维上进行计算 而实际的效果表现在高维上 解决了维度爆炸的问题

线性不可分—高维可分

总结

• 核函数的引入可以避免维度灾难，输入空间的维度n对核函数矩阵没有什么影响，核函数可以处理高维数据
• 核函数可以和不同的算法相结合，形成多种不同的基于核函数技术的方法。

软间隔与正则化

在前面的讨论中，我们一直假设训练样本在样本空间或特征空间食线性可分的，即存在一个超平面能将不同类的样本完全划分开。然而，在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分；退一步说，即便恰好找到了某个核函数使训练样本在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合造成的。

缓解该问题的一个方法是允许支持向量机在一些样本上出错，为此要引入“软间隔”的概念。如图所示

具体来说，前面介绍的支持向量机形式是要求所有样本均满足约束

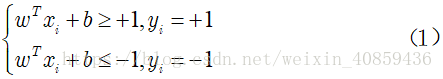
即所有样本都必须划分正确，这称为“硬间隔”，而软间隔则是允许某些样本不满足约束

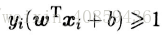
当然，在最大化间隔的同时，不满足约束的样本应尽可能小，于是优化目标可以写为

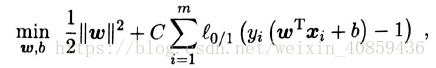
其中，C是一个常数， l0/1是“0/1损失函数”

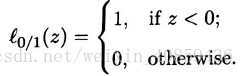
根据KKT条件可推得最终模型仅与支持向量有关, 也 即hinge损失函数依然保持了支持向量机解的稀疏性


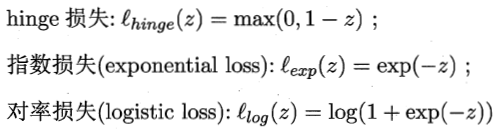
根据KKT条件可推得最终模型仅与支持向量有关, 也 即hinge损失函数依然保持了支持向量机解的稀疏性

支持向量回归

特点: 允许模型输出和实际输出间存在2ε的偏差

损失函数

落入中间2ε间隔带的样本不计算损失, 从而使得模型获得稀疏性

形式化

总结

SVM是非常经典的机器学习算法，在集成学习和神经网络的算法流行之前，SVM在分类领域占据着统治地位。在大数据时代，SVM由于在大样本数据集上的计算量太大，所以热度有所下降，但不失为一个常用的机器学习算法。

SVM算法的优点：

1. 解决高维特征的分类问题和回归问题很有效，在特征维度大于样本数时依然能保持良好的效果；
2. 仅仅依靠支持向量来决定超平面，无需依赖全部数据；
3. 有大量核函数可以使用，从而可以很灵活的来解决各种非线性的分类回归问题；
   样本量不是海量数据的时候，分类准确率高，泛化能力强。

SVM算法的缺点：

1. 如果特征维度远远大于样本点，则SVM表现一般；
2. SVM在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用；
3. 非线性问题的核函数的选择没有通用标准，难以选择一个合适的核函数；
4. SVM对缺失数据敏感。

实验

支持向量机是一个二分分类方法，比较适合判断只有两个类别的分类问题，对于多类别的分类，需要对 SVM 的部分代码进行修改。

从几何意义上看，SVM 的基本思想是找到一个分类的直线（或平面，或者非线性曲线或平面），将两个类别的数据分开。

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

cancer = datasets.load_breast_cancer()
cancer_data =  cancer['data']
cancer_target = cancer['target']

cancer_data_train, cancer_data_test, cancer_target_train, \
    cancer_target_test = train_test_split(cancer_data, cancer_target, test_size = 0.2)
    
# 数据标准化
stdScaler = StandardScaler().fit(cancer_data_train)
cancer_trainStd = stdScaler.transform(cancer_data_train)
cancer_testStd = stdScaler.transform(cancer_data_test)

# 建立 SVM 模型
svm = SVC().fit(cancer_trainStd, cancer_target_train)
print('建立的SVM模型为： \n', svm)

# 预测训练集结果
cancer_target_pred = svm.predict(cancer_testStd)
print('预测前20个结果为：\n', cancer_target_pred[:20])

# 预测和真实一样的数目
print('预测对的结果数目为：' , np.sum(cancer_target_pred == cancer_target_test))