[人工智能]KNN算法与线性分类器

一、图像识别

1、简单介绍

图像识别的核心问题：矩阵。
图像识别的任务就是给定图像即矩阵后，对矩阵去做图像识别，以得到一组概率，以此来判断图像的所属类别。

2、不足之处

图像识别的困难之处：准确率一直提升不上去。准确率提升不了的原因主要有如下几个：
1、图片视角不同：每个事物旋转或者侧视最后的构图都完全不同。
2、图片尺寸大小不统一：相同内容的图片也可大可小。
3、图片变形：很多东西处于特殊的情形下，会有特殊的摆放和形状。
4、光影等干扰/幻象
5、背景干扰
6、同类内的差异：比如同一事物有多种类别，椅子有靠椅、吧椅、餐椅、躺椅等。

3、基本流程

图像识别基本流程：
1、输入：给定K个类别的N张图片，作为计算机学习的训练集。
2、学习：让计算机逐张图片地观察和学习。
3、评估：评价计算机学习的学习成果，评价的方法是给定一些计算机不知道类别的图片让它判别，然后再比对我们已知的正确答案。

二、图像识别算法

1、K最近邻法（KNN）

顾名思义，KNN就是需要找到距离样本最近的邻居，那么这时候就需要有一个标准去衡量怎样才算近，所以需要衡量样本之间的距离。常见的主要有以下三类距离：
1、曼哈顿距离

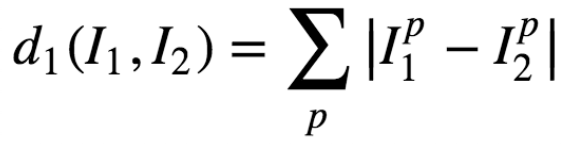
2、欧式距离

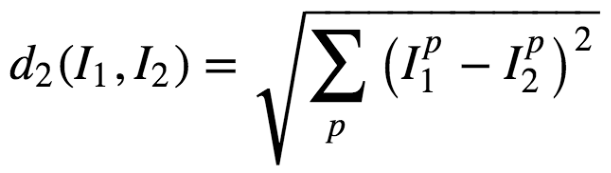
3、余弦距离

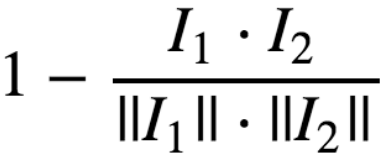
有了距离准则之后，我们可以找到训练集中最近的N个，以他们中最多的类别为结果。例如从1000张图片中挑出与样本图片最接近的5张，如果在挑出的图片中有3张是猫，2张是其它，则此样本图片就被认为是猫。

如上图是原始数据，不同的颜色代表不同的类别，NN就是1NN，即每次只找和它最接近的一张图片，根据这一张图片的类别去判定它现在的类别。5NN是K=5的情况，每次挑最近的5个样本来做一个综合投票，投票最多的结果就标为这个类型。
N折交叉验证：在使用模型时帮我们选择参数。假设现在有一份训练集和一份测试集。我们使用KNN算法时不知道K选择多少，所以要有一个方法去判定K选择多少最合适。数学上是没有合适的公式来帮助我们判定的，我们只能够通过实验得到，验证方式就是N折交叉验证。

如上图所示，例如N=5，就是分成5折，然后轮番的用其中的四折作为真正的训练集，再用第五折做一个交叉验证即评估在训练集上拿到的模型在第五折上的效果怎么样。
交叉验证结果图：

KNN做图像识别缺点：
1、准确度不高
2、要记录全部的训练数据
3、速度比较慢

2、线性分类器

线性分类器会有一个得分函数，例如每张图片是32323，即总共有3072个数，线性分类器要做的事情就是把这3072个数当成x，即x是一个13072的向量，我们会给这个向量x一个权重W。例如让W=103072。假如最后要判定的类别有10种，如上图所示，那么得分函数最后的结果是一个10*1的向量。

如上图所示，如果样本是一张猫的图片，而在此权重下将图片判定成了一条狗，即说明此权重不合适。
对于线性分类器的理解：
1：空间划分

如上图，对于得分函数f(x,W)=Wx+b，当W和b确定后直线也就确定了，就以上图红色的直线函数来说来说，当输入x值代入到红色直线的函数后得到的函数值非常大时，表明在小汽车上方，说明此样本为小汽车的置信度很高。同样，取不同的W，会得到不同的直线，当在其中一条直线上得分非常高时表明接近某一类。
空间划分的效果并不是太好，因为它认为这些东西都是线性可分的。
2、模板匹配

如上图所示，对于每一个得分y${}_i$是由y${}_i$=W${}_i$ x+b${}_i$ 得到，这时把x当作一个输入，W${}_i$一旦确定后就可以看作是一个类别的模板，只不过这时的计算是像素点与模板之间内积的一个计算。意思就是输入x后用不同的W${}_i$去匹配，看哪个匹配度高。

损失函数：

前面我们说过猫的图片识别过后却变成的狗，说明W不是一个合适的权重，所以需要定义一个东西去衡量在现在的W和b下的结果与真实结果的差距有多大，损失函数由此得来。通俗的说就是判断当前的W和b好不好，我们要做的事情就是调整参数W，使得映射结果和实际类别吻合。
损失函数有两种类型：
1、支持向量机损失
对于训练集中的第i张图片x${}_i$，在权重W下会有一个得分函数f(x${}_i$,W)，第j类的得分我们记作f(x${}_i$,W)${}_j$，则在该样本上的损失我们由下列公式计算得到：

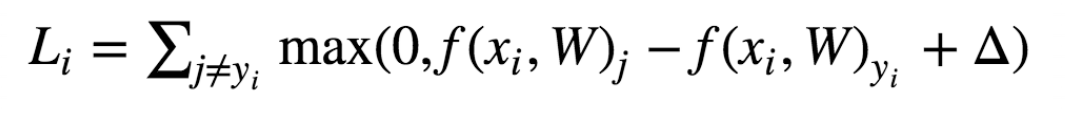
因为是线性模型，因此上式可以简化成如下图所示：

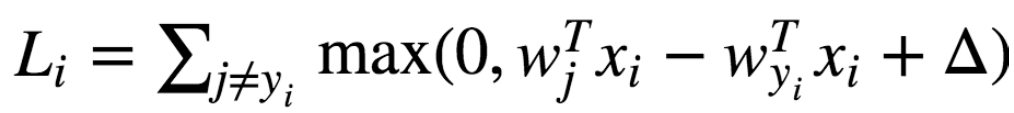
假设我们现在有三个类别猫、狗和船，而得分函数计算某张图片的得分为f(x${}_i$,W)=[13，-7，11]，实际的结果是第一类即这张图片是一只猫。假设$\Delta$=10，上面的公式把错误类别都遍历了一遍，求值加和得到如下：

上述例子损失函数做的事情就是权衡自己判断对的那一类即猫的得分13与判断不对的这两类得分-7与11相比是不是超出了某个量级或者高出了某个给定的$\Delta$。

$\Delta$是超参数，表明我们希望得分向量里判断对的这一类比判断不对的一类至少要多出多少，上例子中猫13是判断对的那一类，max(0,-7-13+10)=0表明在狗这类上没有损失，因为猫得分13比狗得分-7高出了20分，这20分已经满足上诉提出的$\Delta$=10分的要求了，所以这一类没有损失。最后一类船的得分是11，而13只比11多了2，有些接近正确结果，这时衡量在船类别上有损失，因为我们没有满足最小间隔为10的要求。
损失函数2：互熵损失
对于训练集中的第i张图片数据x${}_i$，在W下会有一个得分结果向量f${}_{yi}$，则损失函数记作：

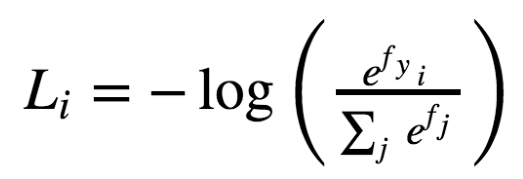
或者

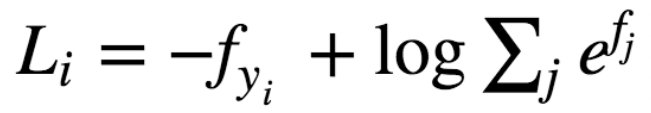
其中一般：

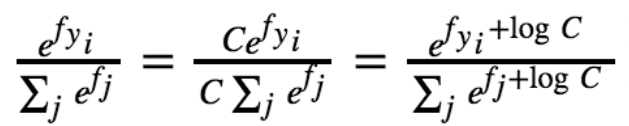
上述损失函数实际上就是先将得分做了一个归一化处理后将得分映射成了概率。例如样本是猫的话正常概率为[1，0，，，0]，而归一化后的概率为[0.6，0.1，，0.1]，互熵损失做的事情就是权衡这两组概率分布之间的差距。