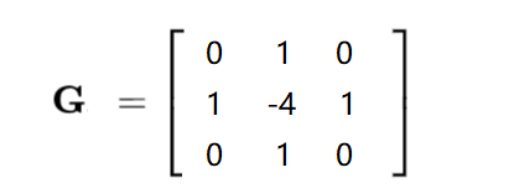图像梯度
梯度:
对于图像,我们选定一定范围(可能是点边界,线边界,闭合边界),对于边界到边界图像像素点像素值的变化我们称之为梯度。
Sobel算子
概念:
Sobel算子主要用于获得数字图像的一阶梯度,常见的应用和物理意义是边缘检测。Sobel算子是把图像中每个像素的上下左右四领域的灰度值加权差,在边缘处达到极值从而检测边缘。
Sobel算子不但产生较好的检测效果,而且对噪声具有平滑抑制作用,但是得到的边缘较粗,且可能出现伪边缘。
核心公式
该算子包含两组3x3的矩阵,分别为横向及纵向,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。如果以A代表原始图像,
G
x
G_x
Gx?及
G
y
G_y
Gy?分别代表经横向及纵向边缘检测的图像,其公式如下:

前者
G
x
G_x
Gx?用于计算水平梯度,而后者
G
y
G_y
Gy?则用于计算垂直梯度。
注意:这里并不是矩阵的乘法,而是卷积即对应位置相乘运算。
图像的每一个像素的横向及纵向梯度近似值可用以下的公式结合,来计算梯度的大小。
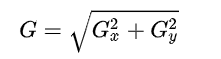
然后可用以下公式计算梯度方向。
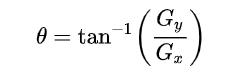
下面介绍Sobel算子的语法:
dst = cv2.Sobel(src, ddepth, dx, dy, ksize)
参数:src就是计算的图像,ddepth为图像的深度,dx,dy表示是水平方向还是竖直方向,ksize表示Sobel算子的大小即上述进行矩阵卷积运算的矩阵规格大小。
这里给大家展示以下图像经过梯度运算的效果:
原图像:

经过梯度运算
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
得到的图像:

这里我们可以看到dx我们取为1dy取0表示进行的是进行水平梯度运算,而我们发现运算过后的图像“边缘”,好像仅有原图的一半。那是因为通过Sobel算子的公式我们可以看到,对于水平梯度计算简单的看做右边减左边,对于原图的左边缘,边缘左边为黑即像素值为0,右边为白即像素值为255,进行运算得到边缘的像素值为正,而对于右边边缘,右边边缘的左边为255右边为0,进行运算得到的像素值为负,而在Opencv中会默认做一个截断,即凡小于0的像素值均取0,所以右半边边缘经过梯度计算后全部为0即为黑色不做显示。
我们可以通过Opencv中取绝对值的方法来得到完整边缘,下面展示竖直方向取过绝对值之后的计算结果
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3)#竖直方向梯度计算
sobely = cv2.convertScaleAbs(sobely) #取绝对值

这里是不建议dx与dy即水平与垂直同时进行计算,因为这两种计算的计算结果都会影响彼此,从而使进行梯度运算变得模糊,在直观上好像是水平梯度与竖直梯度“融合的不太好”。
sobelxy=cv2.Sobel(img,cv2.CV_64F,1,1,ksize=3)
sobelxy = cv2.convertScaleAbs(sobelxy)

如果有需要我们可以直接通过Opencv自带的加权加法进行合并两图。
Scharr算子和laplacian算子
Scharr算子
Scharr算子整体思路与Sobel算子没有区别,但是在计算上Scharr算子公式中数值更大,更加注重规定方向的影响,弱化了边缘(矩阵边缘不是图像边缘)的影响。
Scharr算子的计算公式
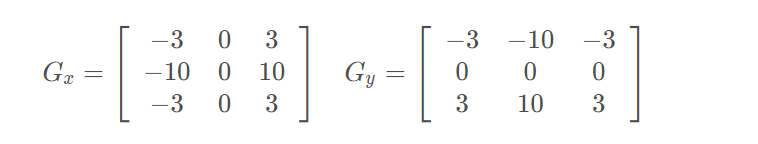
laplacian算子
laplacian算子具体思想与推导比较复杂就不给大家做演示了,它与前面提到的算子主要区别是前面算子都停留在一阶导的层面,而laplacian算子中提到了二阶导,所以laplacian算子相比于前面的算子会对“变化”会更加敏感,展现出来“变化”较大的地方会更加明显,但是因为对变化过于敏感,所以对于噪音点laplacian算子处理就不是很好,所以laplacian算子通常不会单独使用。
由公式也可以看出laplacian算子更注重于变化而不是强调方位。
laplacian算子的计算公式