目录
序列模式挖掘简介
序列模式的概念最早是由Agrawal和Srikant提出的。
动机:大型连锁超市的交易数据有一系列的用户事务数据库,每一条记录包括用户的ID,事务发生的时间和事务涉及的项目。如果能在其中挖掘涉及事务间关联关系的模式,即用户几次购买行为间的联系,可以采取更有针对性的营销措施。
事务数据库实例 例:一个事务数据库,一个事务代表一笔交易,一个单项代表交易的商品,单项属性中的数字记录的是商品ID

序列数据库
一般为了方便处理,需要把数据库转化为序列数据库。方法是把用户ID相同的记录合并,有时每个事务的发生时间可以忽略,仅保持事务间的偏序关系。

问题定义
项集(Itemset)是所有在序列数据库出现过的单项组成的集合
例:对一个用户购买记录的序列数据库来说,项集包含用户购买的所有商品,一种商品就是一个单项。通常每个单项有一个唯一的ID,在数据库中记录的是单项的ID。
元素(Element)可表示为(x1x2...Xm),X k(1 <=k<= m)为不同的单项。元素内的单项不考虑顺序关系,一般默认按照ID的字典序排列。
在用户事务数据库里,一个事务就是一个元素。
序列(Sequence)是不同元素(Element)的有序排列,序列s可以表示为s =<S, S2.….Sl>,s(1 <=j<=l)为序列s的元素
一个序列包含的所有单项的个数称为序列的长度。长度为l的序列记为l-序列 例:一条序列<(10,20) 30(40, 60,70)>有3个元素,分别是(10 20),30,(40 60 70)
3个事务的发生时间是由前到后。这条序列是一个6-序列。
设序列α = <a1a2...an>,序列β=<b,b2.. .bm>,ai和bi,都是元素。
如果存在整数1<=j1<j2<...<jn<= m,使得a1?bj1,a2?bj2,..., an?bjn,则称序列α为序列β的子序列,又称序列β包含序列a,记为α?β。
序列α在序列数据库S中的支持度为序列数据库S中包含序列α的序列个数,记为Support(α) 给定支持度阈值x,如果序列α在序列数据库中的支持数不低于x,则称序列α为序列模式 长度为l的序列模式记为l-模式。
例子:设序列数据库如下图所示,并设用户指定的最小支持度min-support = 2。

序列<a(bc)df>是序列<a(abc)(ac)d(cf)>的子序列
序列<(ab)c>是长度为3的序列模式
序列模式挖掘的应用背景
应用案例:客户购买行为模式分析
B2C电子商务网站可以根据客户购买记录来分析客户购买行为模式,从而进行有针对性的营销策略。

应用案例:疾病诊断
医疗领域的专家系统可以作为疾病诊断的辅助决策手段。对应特定的疾病,众多该类病人的症状按时间顺序被记录。自动分析该记录可以发现对应此类疾病普适的症状模式。每种疾病和对应的一系列症状模式被加入到知识库后,专家系统就可以依次来辅助人类专家进行疾病诊断。
例:通过分析大量曾患A类疾病的病人发病记录,发现已下症状发生的序列模式:<(眩晕)(两天后低烧37-38度)>
如果病人具有以上症状,则有可能患A类疾病
序列模式挖掘算法概述
类Apriori算法
该类算法基于Apriori理论,即序列模式的任一子序列也是序列模式。算法首先自底向上的根据较短的序列模式生成较长的候选序列模式,然后计算候选序列模式的支持度。典型的代表有GSP算法,spade算法。
基于划分的模式生长算法
该类算法基于分治的思想,迭代的将原始数据集进行划分,减少数据规模,同时在划分的过程中动态的挖掘序列模式,并将新发现的序列模式作为新的划分元。典型的代表有FreeSpan算法,prefixSpan算法。
GSP算法
算法思想
1、扫描序列数据库,得到长度为1的序列模式,作为初始的种子集L1。
2、根据长度为i的种子集Li,通过连接操作和修建操作生成长度为i+1 的候选序列模式Ci+1;然后扫描序列数据库,计算每个候选序列模 式的支持度,产生长度为i+1的序列模式Li+1,并将Li+1作为新的 种子集。
3、重复第二步,直到没有新的序列模式或新的候选序列模式产生 为止。
产生候选序列模式的步骤
?1、连接阶段:如果去掉序列模式S1的第一个项目与去掉序列模式 S2的最后一个项目所得到的序列相同,则可以将S1与S2进行连接 ,即将S2的最后一个项目添加到S1中。
2、剪切阶段:若某候选序列模式的某个子序列不是序列模式, 则此候选序列不可能是序列模式,将它从候选序列模式中删除。
哈希树
GSP采用哈希树存储候选序列模式。哈希树的节点分为三类: 1、根节点 2、内部节点 3、叶子节点 根节点和内部节点中存放的是一个哈希表,每个哈希表指向其他的节点。而叶子节点内存放的是一组候选序列模式?。

时间约束计算
这个是用在支持度计数使用的,GSP算法的支持度计算不是那么简单,比如序列判断<2, <3, 4>>是否在序列<(1,5), 2 , <3, 4>, 2>,这就不能仅仅判断序列中是否只包含2,<3, 4>就行了,还要满足时间间隔约束,这就要把2,和<3,4>的所有出现时间都找出来,然后再里面找出一条满足时间约束的路径就算包含。时间的定义是从左往右起1.2,3...继续,以1个项集为单位,所有2的时间有2个分别为t=2和t=4,然后同理,因为<3,4>在序列中只有1次,所以时间为t=3,所以问题就变为了下面一个数组的问题
2 ?4
3
从时间数组的上往下,通过对多个时间的组合,找出1条满足时间约束的方案,这里的方案只有2-3,4-3,然后判断时间间隔,如果存在这样的方式,则代表此序列支持所给定序列,支持度值加1,这个算法在程序的实现中是比较复杂的。
时间约束计算案例分析
现假设最大事务时间间隔maxgap=30,最小事务时间间隔mingap=5,考察候选数据序列s=<(1,2)(3)(4)>是否包含在该数据序列中

?
?GSP算法优缺点
优点: 1)GSP引入了时间约束,增加了扫描的约束条件,有效地减少了需要扫描的候选序列的数量,减少多余的无用模式的产生。 2)GSP利用哈希树来存储候选序列,减小了需要扫描的序列数量
缺点: 1)如果序列数据库规模较大,则有可能产生大量的候选序列模式; 2)需要对序列数据库进行循环扫描; 3)对于序列模式的长度比较长的情况,算法难以处理。
PrefixSpan算法
基于划分的模式生长算法
该类算法基于分治的思想,迭代的将原始数据集进行划分,减少数据规模,同时在划分的过程中动态的挖掘序列模式,并将新发现的序列模式作为新的划分元。典型的代表有FreeSpan算法和prefixSpan算法
PrefixSpan算法的一些概念
前缀∶对于序列A={a1,a2,.….an}和序列B={b1,b2,.…. bm} n<=m,满足a1=b1,a2= b2…an-1 = bn-1,而an?bn,则称A是B的前缀。比如对于序列B=<a(abc)(ac)d(cf)>,而A=<a(abc)a>,则A是B的前缀。当然B的前缀不止一个,比如<a>,<aa>, <a(ab)>也都是B的前缀。
投影:给定序列α和β,如果β是α的子序列,则α’关于β的投影α’必须满足: β是α’的前缀, α’是α的满足上述条件的最大子序列。 ? ? ?
比如:序列α =<(ab)(acd)>,其子序列β=<(b)>的投影是α’= <(b)(acd)>; <(ab)>的投影是原序列<(ab)(acd)>。
前缀投影(后缀)︰对于某一个前缀,序列里前缀后面剩下的子序列即为后缀。如果前缀最后的项是项集的一部分,则用一个“_”来占位表示。
设最小支持度为25%,即最小支持计数 ? ?(5x25%=1.25,取上整为2)
序列<a,(abc),(ac),d,(cf)>的前缀和前缀投影前缀
| 前缀 | 前缀投影 |
| <a> | <(abc),(ac),d,(cf)> |
| <a,a> | <(_bc),(ac),d,(cf)> |
| <a,b> | <(_c),(ac),d,(cf)> |
PrefixSpan算法思想
它从长度为1的前缀开始挖掘序列模式,搜索对应的投影数据库得到长度为2的前缀。搜索长度为2的前缀对应的投影数据库,得到长度为3的前缀。...以此类推,一直递归到不能挖掘到更长的前缀,挖掘为止。
算法步骤
1 )对数据库中所有的项进行支持度统计,将支持度低于阈值的项从数据库中删除,得到长度为1的前缀
2)对于每个长度为i满足支持度要求的前缀进行递归挖掘∶ ? ? ? ?
? ? ? ?a)找出前缀所对应的投影数据库。如果投影数据库为空,则递归返回。 ? ? ? ?
? ? ? ?b)统计对应投影数据库中各项的支持度计数。如果所有项的支持度计数都低于阈值α,则递归返回。 ? ? ? ?
? ? ? ?c)将满足支持度计数的各个单项和当前的前缀进行合并,得到若干新的前缀。 ? ? ?
? ? ? ?d)令i=i+1,前缀为合并单项后的各个前缀,分别递归执行第2步。
例子:
| SID | 序列 |
| 1 | <(AB),B,C> |
| 2 | <(AC),(ABC),B> |
| 3 | <A,B> |
| 4 | <(AB),A,B> |
设置支持度阈值为:3
(1)对数据库中所有的项进行支持度统计,将支持度低于阈值的项从数据库中删除,得到长度为1的前缀
| A | B | C |
| 4 | 4 | 2 |
| SID | 序列 |
| 1 | <(AB),B> |
| 2 | <(A),(AB),B> |
| 3 | <A,B> |
| 4 | <(AB),A,B> |
(2)对于每个长度为1满足支持度要求的前缀进行递归挖掘:
| A | |
| 1 | <(_B),B> |
| 2 | <(AB),B> |
| 3 | <B> |
| 4 | <(_B),A,B> |
| A | B | _B |
| 2 | 4 | 3 |
?新前缀:<A,B> ? <(AB)>
| B | |
| 1 | <B> |
| 2 | <B> |
| 3 | <B> |
| 4 | <A,B> |
| A | B |
| 1 | 3 |
新前缀:<B,B>
(3)重复第二步
| <(AB)> | |
| 1 | <B> |
| 2 | <B> |
| 3 | <> |
| 4 | <A,B> |
| A | B |
| 1 | 3 |
新前缀:<(AB),B>
PrefixSpan算法总结
PrefixSpan算法由于不用产生候选序列,且投影数据库缩小的很快,内存消耗比较稳定,作频繁序列模式挖掘的时候效果很高。比起其他的序列挖掘算法比如GSP,FreeSpan有较大优势,因此是在生产环境常用的算法。
PrefixSpan运行时最大的消耗在递归的构造投影数据库。如果序列数据集较大,项数种类较多时,算法运行速度会有明显下降。因此有一些PrefixSpan的改进版算法都是在优化构造投影数据库这一块。比如使用伪投影计数。
当然使用大数据平台的分布式计算能力也是加快PrefixSpan运行速度一个好办法。比如Spark的MLlib就内置了PrefixSpan算法。
不过scikit-learn始终不太重视关联算法,一直都不包括这一块的算法集成,这就有点落伍了。
优点: 1)不产生任何的候选集,减少空间; 2)投影数据库规模不断减少(因为投影仅发生在与前缀相关的后缀部分);
缺点: 1)算法主要开销在于投影数据库的构造; 2)实现难度较大
Spade算法
GSP算法在每次计算序列的支持度时,都需要扫描一遍数据库。
可不可以通过遍历一次数据库的经验知识来降低多次对数据库的扫描呢?
Spade提出了ID_LIST的概念,来避免多次对数据库进行全表扫描的问题。ID_LIST是一个(SID, EID)组成的表
SPADE算法是GSP算法的改进,它在扫描的时候不是扫描整个数据库,而是扫描ID_LIST。
算法步骤
扫描序列数据库,生成所有的1-序列,并将数据转成垂直的存储方式。统计各序列对应的支持度计数,小于规定支持度的排除。
当前1-序列构成2-序列的原子项,通过频繁1-序列的自连接操作产生2-序列的候选序列,并进一步得到频繁2-序列。
当前频繁2-序列构成了3-序列的原子项,通过频繁2-序列的自连接操作产生3-序列的候选序列,并进一步得到频繁3-序列。
实际案例


NOTE:“EID”表示事务发生时间
?假设:支持度阈值设为3
1-序列的ID_LIST



? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?note:红色框代表非频繁序列
?2-序列的ID_LIST
?




<A,A> 是由1频繁序列A的ID_list生成的;
<A,B> 是由1频繁序列A的ID_list和1频繁序列B的ID_list生成的;
<(A,B)> 也是由1频繁序列A的ID_list和1频繁序列B的ID_list生成的
?3-序列的ID_LIST



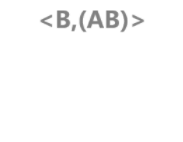
<A,(AB)> 没有生成ID_list,因为<A,A> 是非频繁的; <B,(AB)> 没有生成ID_list,因为 <B,A> 是非频繁的;
SPADE算法总结
SPADE算法通过遍历一次数据库得到的经验知识来降低多次对数据库的扫描。
优点:
1)避免对原始数据进行扫描,序列越长,处理速度越快;
2)SPADE不仅通过减少对数据库的扫描降低I/O成本,而且通过搜索ID_list降低计算成本;
3)没有采用哈希树,因此具有很好的局域性。
缺点:
1)候选集过多;
2)实现难度相较于GSP算法来说要大一些
?
?
?
?
?
?
?
?
?