[人工智能]因果推断笔记——解析一篇因果反事实预测论文（二十三）

反事实预测应该是一个非常有意思的话题，笔者也是由一篇盒马的文章出发，对这个模块先行进行简答的学习。主要参考：
KDD2021论文推荐：盒马-融合反事实预测与MDP模型的清滞销定价算法
Markdowns-in-E-Commerce-Fresh-Retail-A-Counterfactual-Prediction-and-Multi-Period-Optimization-Approach

盒马这篇论文的地址：
https://arxiv.org/pdf/2105.08313.pdf

这个团队另外一篇也很给力，是非常通用的营销预测框架类，很给力了：
预算分配Budget Allocation：两篇论文（二）

关联文章：
因果推断笔记——DML ：Double Machine Learning案例学习（十六）

利用机器学习因果推理进行弹性定价
数据分析36计(29)：价格需求弹性和因果推断
简单版：DML.ipynb
数据集：Association Rules and Market Basket Analysis

1 已有研究者的描述

1.1 YuyangZhangFTD

来看来自zhangyuguo的对该篇的解读：
Markdowns-in-E-Commerce-Fresh-Retail-A-Counterfactual-Prediction-and-Multi-Period-Optimization-Approach

这篇文章中了KDD2021，是做阿里盒马生鲜的折扣定价问题。

我个人很早之前也关注过电商商品定价的问题，之前看过比如说rue lala、一号店、zara的一些动态定价的方法，心里有些比较模糊的想法，当时想的大概是用choice-model来刻画商品互补替代效应的同时，加入价格的影响，然后在某个周期内求解最优化模型。由于种种原因，当时并没有深入思考算法细节以及针对实际问题进行实践，这类问题主要有三个比较棘手的问题：

• 在只有观测数据的时候，怎么构建价格弹性，现在来看这就是一个反事实推断的问题，不仅是如何做的问题，还有如何评估的问题
• 长周期的规划决策问题怎么建模 & 求解，如何在决策优化中考虑不确定性
• 这种pricing的问题，在现实世界中如何做A/B、如何科学评估效果

这篇文章有很多细节&落地的工作，本文的几个主要贡献：

• 是用了一种半参数结构的模型来学习个体的价格弹性，并给出反事实的需求预测，这种模型能够同时具有非参数机器学习模型的预测能力和经济学模型的可解释性
• 提出了一种多阶段的动态定价算法来最大化有保质期商品整个销售周期内的销售利润，与采用确定性需求的传统做法不一样的是，本文的模型中考虑了反事实销量预测的不确定性，采用了连续的定价策略，并且设计了一种两阶段的算法求解

1.1.1 Introduction

在生鲜零售的场景，商品的新鲜程度是消费者最关心的问题，很多有保质期的商品，比如说蔬菜、肉类、鸡蛋、面包，都是只有有限的销售周期，为了提供新鲜、高质量的商品，控制库存就变得十分重要，如果一个商品在过期之前还没有卖完，那么零售商就会有损失，生鲜零售商往往会采用促销的手段来最大化总利润，但却很难知道最优的价格折扣是什么。

本文中，我们考虑有两种渠道销售商品的生鲜零售商，其中一个是正常价格销售，另一个渠道是折扣商品，其中消费者可以在购满一定销售额的基础上，以一定折扣购买商品。

1.1.2 Problem Formulation

• 零售价格折扣$d\in [0,1]$为我们的决策变量
• 产品$i$在折扣$d_i$上的平均销量$Y_i^{\text{obs}}$
• 特征$x_i\in {\mathbb{R}}^n$
• 类别特征$L_i\in {0,1}^m$，假设有3级类别

1.1.3 Counterfactual Prediction

反事实预测问题的目标是在干预$d_i$和条件$X=x_i$下预估需求/销量
的期望$\mathbb{E}[Y_i|do(d_i),x_i]$，此处我们假设满足unconfoundness假设。

因为历史上一个商品很少有多种折扣的数据，所以我们无法拟合单个商品的价格需求函数，为了解决这个问题，我们使用数据聚合的方式，我们把所有商品用类目信息进行聚合，然后联合学习多个商品的价格弹性。

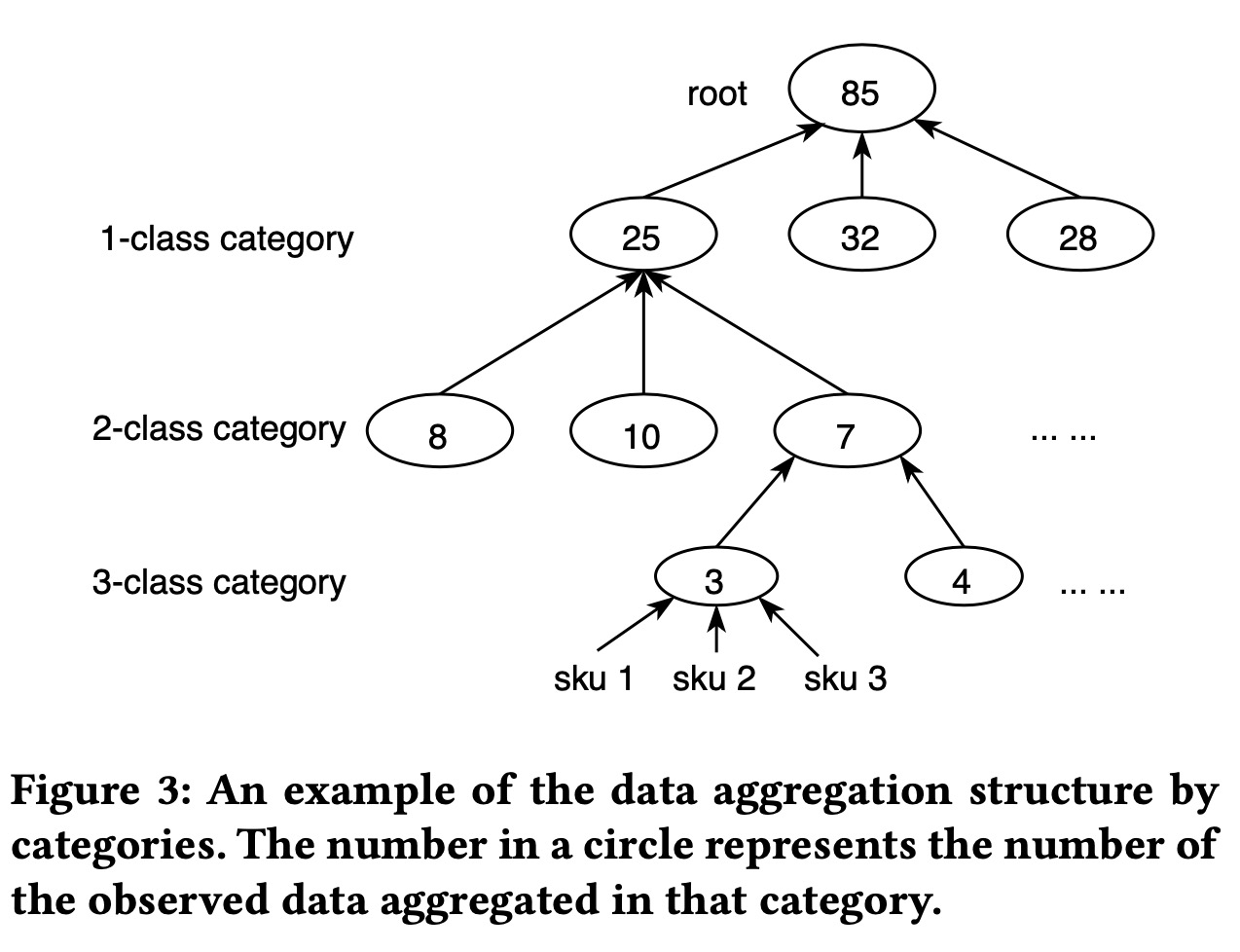
我们假设模型结构为

$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=g(d_i;L_i,\theta )+h(d_i^{\text{o}},x_i)?g(d_i^{\text{o}};L_i,\theta )$

其中：

• $Y_i^{\text{o}}$是常规渠道产品$i$近期的平均销量
• $d_i^{\text{o}}$是商品$i$近期的平均折扣
• $Y_i/Y_i^{\text{nor}}$代表了折扣价格使得销量增加的百分比，因为不同商品销量差异很大，所以比率会比绝对值更有用
• 函数$g(d_i;L_i,\theta )$是参数化的价格弹性模型，参数$\theta \in {\mathbb{R}}^{m+1}$
• 函数$h(d_i^{\text{o}},x_i)$为非参数预测模型，用于预测基础折扣$d_i^{\text{o}}$的销量，如果$d_i=d_i^{\text{o}}$，那么$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})|d_i^{\text{o}}]=h(d_i^{\text{o}},x_i)$

对于价格弹性，我们提出一种双log结构的nested模型:

$g(d_i;L_i,\theta )=\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=({\theta }_1+{\theta }_2^{\mathsf{T}}{L}_i)\ln d_i+c$

其中${\theta }_2\in {\mathbb{R}}^m$，$\theta =[{\theta }_1,{\theta }_2^{\mathsf{T}}{]}^{\mathsf{T}}$，$c$为截距参数，$L_i$为由三级one-hot变量组成

$L_i=[\underset{\text{category?1}}{0,?,1,0},\underset{\text{category?2}}{0,1,?,0},\underset{\text{category?3}}{0,?,0,1},{]}^{\mathsf{T}}$

通过指数转换，模型可以写作:

$Y_i=Y_i^{\text{nor}}{e}^c{d}_i^{{\theta }_1+{\theta }_2^{\mathsf{T}}{L}_i},?i$

其中${\theta }_1+{\theta }_2^{\mathsf{T}}{L}_i$就是价格弹性，所以每个独立SKU的价格弹性是由类别的价格弹性组成的。

为了顾及价格弹性，我们用所有样本最小化均方误差来拟合模型，在现实电商场景中，一个更好的方式是在线实时更新参数：

$\underset{\theta ,c}{\min }{\sum }_{i=1}^N{\sum }_{j=1}^t{\tau }^{t?j}\Vert \ln \frac{Y_{i,j}}{Y_{i,j}^{\text{nor}}}?{\theta }^{\mathsf{T}}{\hat{L}}_i\ln d_{i,j}?c{\Vert }_2^2+\lambda \Vert \theta {\Vert }_2^2$

其中$\lambda >0$是正则系数，$0<\tau \le 1$为忘记因子，为了避免较遥远历史数据的影响。

最终的预测模型为

$\ln Y_{i,t}(d_i)={\hat{\theta }}_t^{\mathsf{T}}{L}_i(\ln d_i?\ln d_{i,t}^{\mathsf{o}})+\ln Y_{i,t}^{\mathsf{o}}$

此处只是建模了商品的价格弹性，忽略了商品之间的互补替代效应。

1.1.4 excample of problem

商品价格为$p_0$，这个价格是常规渠道的销售价格，且价格固定，用$d_t$表示商品在周期$t$时的折扣，对应的价格为$p_t=p_0{d}_t$，我们对于常规渠道的销量预测为$Z_{j,t}，?j,t$，反事实的销量预测为$Y_{jt}(d_t)$，同时考虑到最后浪费的损失，优化问题为：

$\begin{array}{rl}\underset{d_1,?,d_T}{\max }& \sum _{j\in \mathcal{J}}(\sum _{t=1}^{T_j}{p}_0{d}_t{Y}_{jt}(d_t)?w_j[B_j?\sum _{t=1}^{T_J}(Y_{jt}(d_t)+Z_{jt}){]}^{+})\\ \text{s.t.}& \sum _{t=1}^{T_j}(Y_{jt}(d_t)+Z_{jt})\le B_j?j\in \mathcal{J}\\ & l{b}_{jt}\le p_t\le u{b}_{jt}?t=1,\dots ,T_j,j\in \mathcal{J}\end{array}$

其中$w_j$是浪费损失的权重，$[?{]}^{+}$为非负运算符，$l{b}_{jt}$和$u{b}_{jt}$是折扣最大和最小的上下限制，因为$Z_{jt}$和$B_j$是独立于决策变量的，所以可以简化上述问题为：

$\begin{array}{rl}\underset{d_1,?,d_T}{\max }& \sum _{j\in \mathcal{J}}\sum _{t=1}^{T_j}(p_0{d}_t+w_j)Y_{jt}(d_t)\\ \text{s.t.}& \sum _{t=1}^{T_j}(Y_{jt}(d_t)+Z_{jt})\le B_j?j\in \mathcal{J}\\ & l{b}_{jt}\le p_t\le u{b}_{jt}?t=1,\dots ,T_j,j\in \mathcal{J}\end{array}$

对于上面这个问题，我们并不准备直接求解，考虑到可以打的折扣是是有限的，我们将这个问题转化成离散优化问题。虽然模型已经给出了$Y_{jt}(d_t)$和$Z_{jt}$的预估，但是仍会有随机的误差，所以我们需要考虑上述问题的不确定性，我们用MDP来建模整个决策过程。

定义每个门店$j$在常规渠道和折扣渠道的真实销量为$a_{jt}^y$和$a_{jt}^z$，用$s_{jt}$表示商品$t$时刻在门店$j$的库存：
$\begin{array}{rl}{s}_{j,1}& =B_j\\ s_{j,t+1}& =s_{j,t}?a_{j,t}^y?a_{jt}^z,t<T_j\\ s_{j,t+1}& =0T_j\le t\le T_{m}ax\end{array}$

其中$s_{jt}$是个单调递减的序列，候选折扣集合
D = { d 1 , ? ? , d M } \mathcal{D}=\{d^1, \cdots,d^M\} D={d1,?,dM}。

为了建模销量的不确定性，我们从历史数据中发现，大部分情况下销量服从泊松分布，期望参数为$Y_{jt}(d_t)$和$Z_{jt}$（此处假设$Y_{jt}(d_t)$和$Z_{jt}$是$a_{jt}^y$和$a_{jt}^z$的无偏估计）

定义$a_{jt}=a_{jt}^y+a_{jt}^z$，销量不会高于库存，所以我们定义状态转移矩阵

$\begin{array}{r}P(s_{j,t+1}|s_{j,t},d_t)=\{\begin{array}{ll}\text{Poi}(s_{j,t}?s_{j,t+1}|Y_{jt}(d,t)+Z_{jt})& 0<s_{j,t+1}\le s_{j,t}\\ 1?Q(s_{j,t}?1,Y_{jt}(dt)+Z_{jt})& s_{j,t+1}=0\end{array}\end{array}$

期望状态转移后的奖励为

$R(s_{j,t},d_t,s_{j,t+1})=(p_0{d}_t,+w_j)[s_{j,t}?s_{j,t+1}?Z_{jt}{]}^{+}$

所以多阶段的优化问题变成一个选择策略$\pi (?)$来最大化累计奖励的问题

${\sum }_{j\in \mathcal{J}}{\sum }_{t=1}^{T_j}R(s_{j,t},d_t,s_{j,t+1}),d_t=\pi (s_t)$

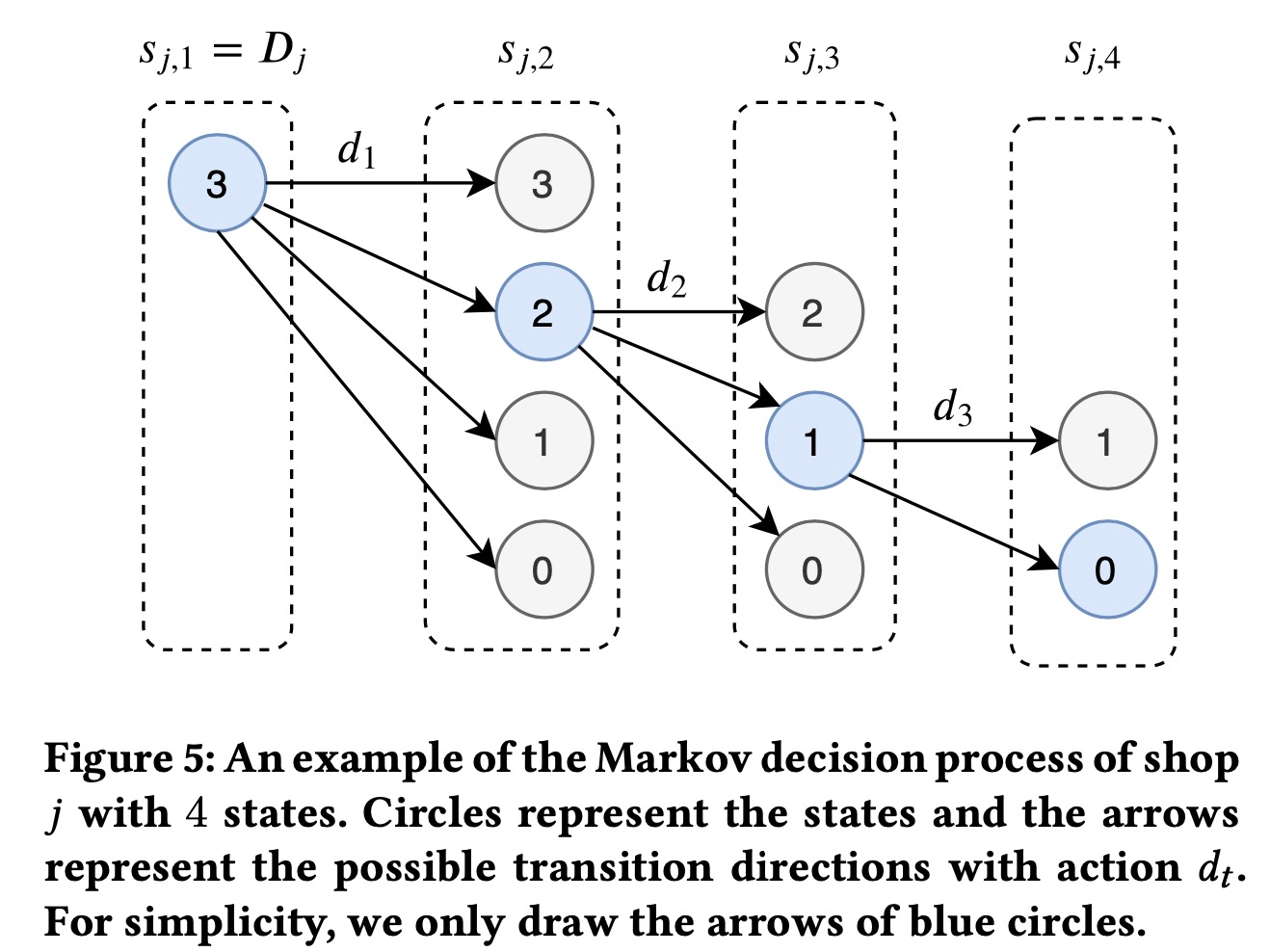
为了求解这个MDP的问题，我们提出了一种两阶段的算法，分开反向求解和联合优化两步：

对于每个门店，单独进行更新
$Q(s_{j,t},d_t)={\sum }_{s_{j,t+1}=0}^{s_{j,t}}P(s_{j,t+1}|S_{j,t},d_t)?(R(s_{j,t},d_t,s_{j,t+1})+{\max }_{d_{t+1}\in \mathcal{D}}Q(s_{j,t+1},d_t)),t=2,?T_j,j\in \mathcal{J}$

联合优化，对于所有店铺联合优化，并在单个阶段求最优
$d_1^{?}=\underset{d_t\in \mathcal{D}}{\mathrm{argmax}}{\sum }_{j\in \mathcal{J}}Q(s_{j,1}=B_j{,}_t)$

所以我们可以得到最优定价$p_1^{?}=p_0{d}_1^{?}$，因为这个算法每天会重新更新训练，所以只需要每天重新计算第一阶段的最优值。

1.1.5 Experiment

文中对比了不同模型：Xgb、DeepIV和提出的结构化的回归模型:

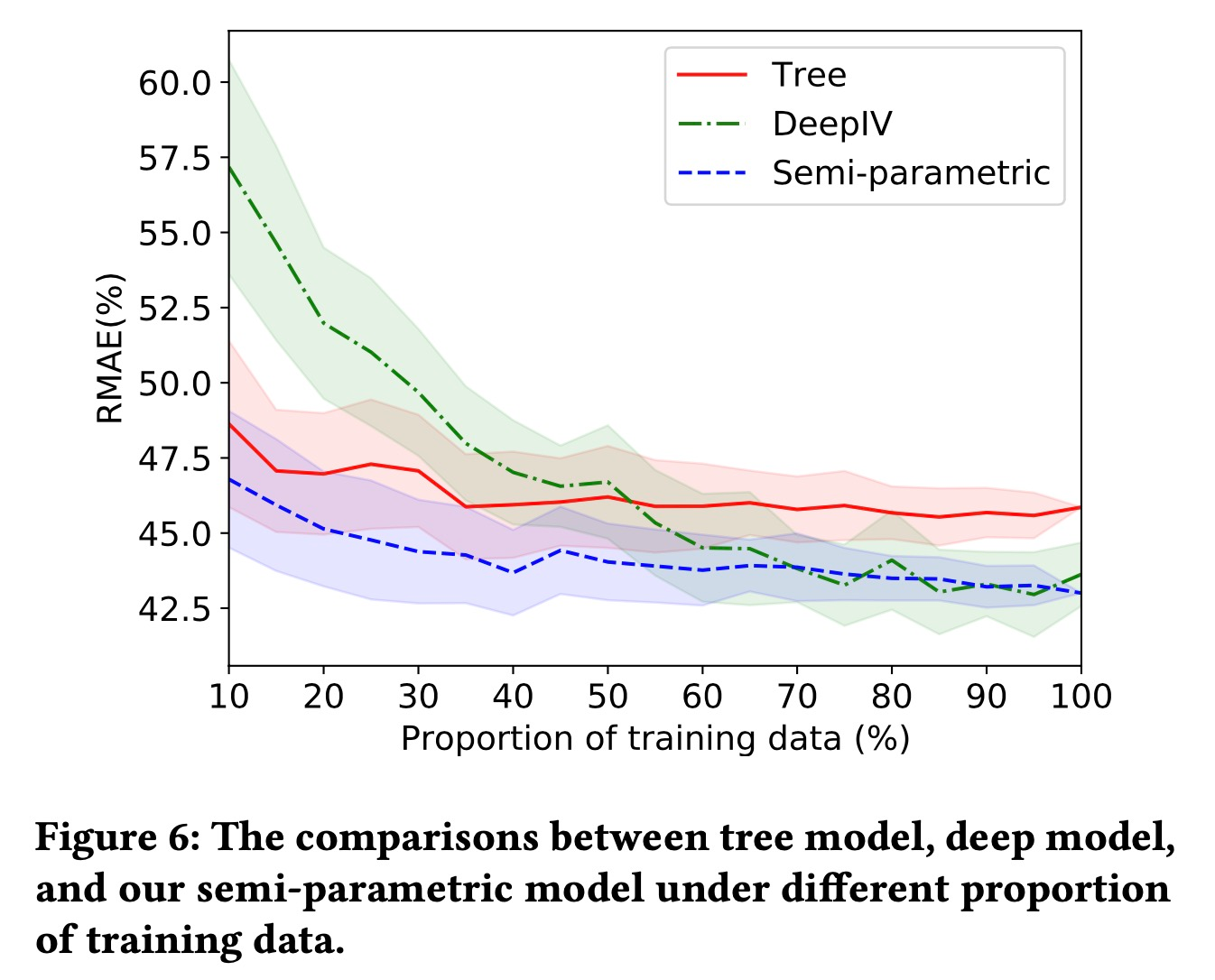
1.1.6 train _ price-sale curve

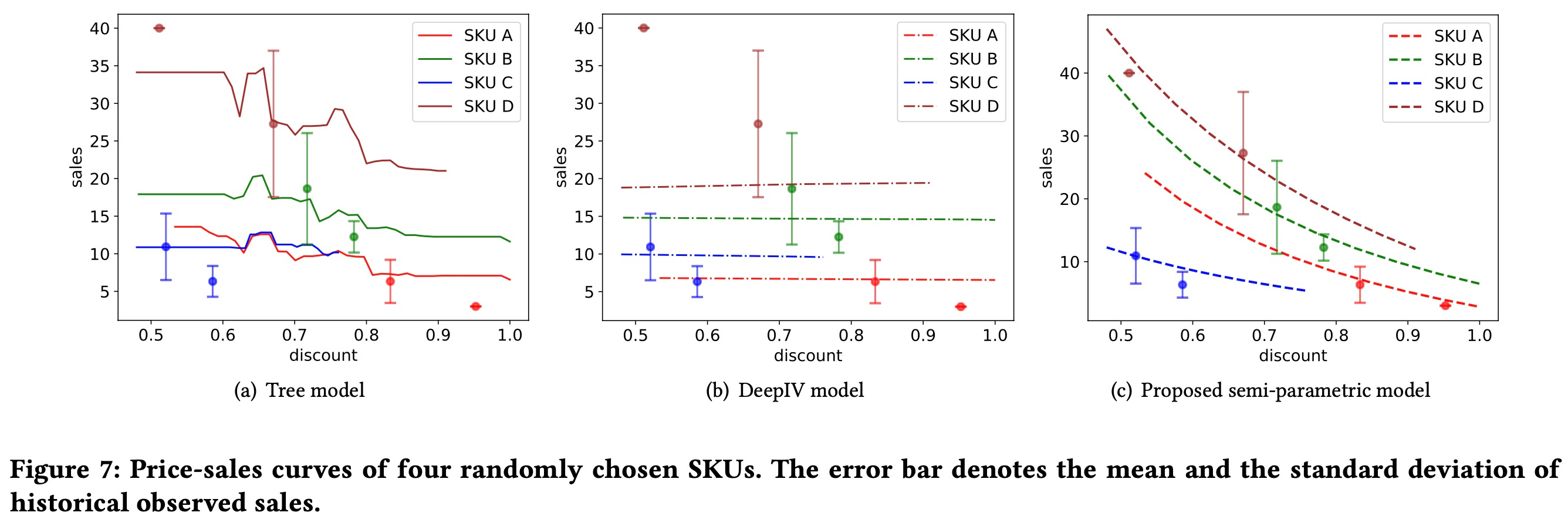
1.1.7 ab测试

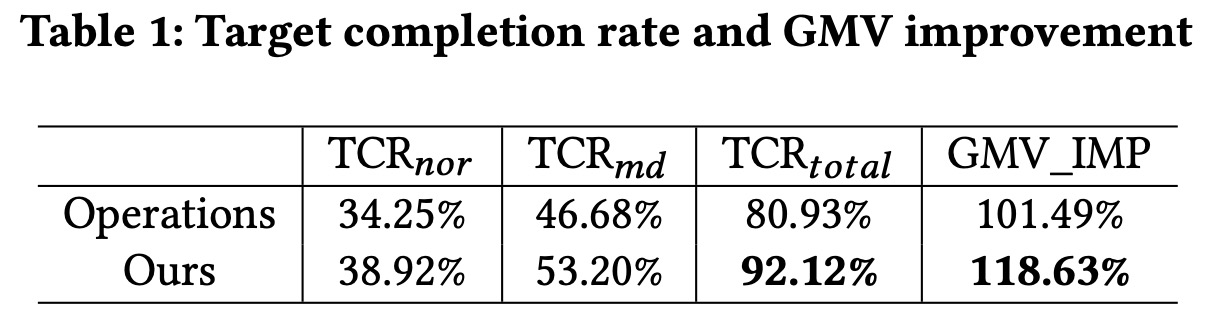
1.1.8 一些想法

论文内容部分讲完了，总体是一篇很踏实的文章，一个业务有接近20%的GMV提升，可以说是非常“有效”的解决了问题，但这篇文章仍然有些缺点，或者说没有放在论文里的点，再回顾一下最开始的三个问题：

• 没有直面反事实学习和评估的问题，只是通过加入对于价格弹性的人工知识先验（选择模型+类目分层的关系）来规避这个问题，文中提到的price-sales curve，虽然看着结果很好，但实际上也不能算是非常靠谱的评估。
• 在做多阶段的优化时候，仍然是忽略了不同阶段预测模型效果的差异，T+1和T+N时候的预测，方差是逐渐变大的，如何建模这部分的不确定性，并没有细说。
• 没有具体写AB实验怎么做的，是时间片还是分门店，还是线上用户分流，这些都没有详细写清楚，有很多容易受到challenge的点，这种业务如何科学合理的做实验仍是一个复杂且充满挑战的问题。

1.2 知乎：斑马

KDD2021论文推荐：盒马-融合反事实预测与MDP模型的清滞销定价算法

研究问题：如何动态决策滞销商品（在保质期内无法以原价销售完）的折扣力度以获取最大收益？滞销定价策略通过在商品生命周期的不同阶段动态调整折扣额以实现库存成本的降低和 GMV 收益的提升。滞销品定价所面临的核心问题在于商品历史价格点稀疏且噪声较大导致难以确定合适的价格。

产品形态：盒马App的商品销售页面有2种，一种是商品原价的正常频道页，一种是满x元换购折扣商品的降价频道页。

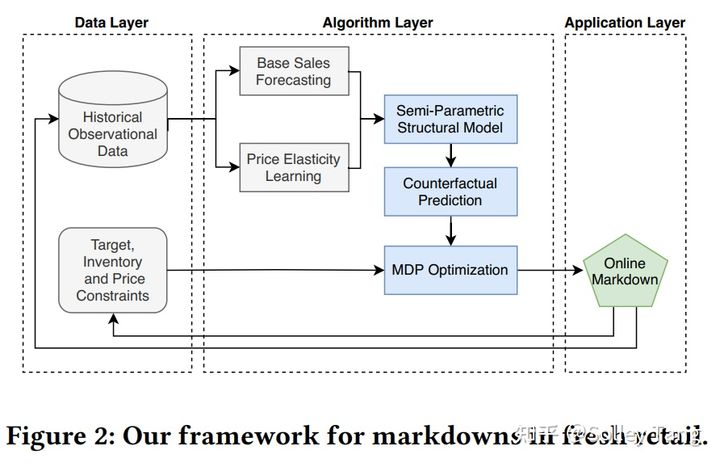
1.2.1 整体框架和技术亮点

整体思路/框架：将滞销商品定价流程拆解为两步，

• 第一步：基于观测数据搭建半参数模型建模折扣和销量之间的因果关系，实现需求弹性的反事实预测：其中参数模型假设的存在提升了反事实预测的泛化性，解决了观测数据稀疏性问题，从而能够得到不同折扣额的销量预估，同时兼顾了一定的模型可解释性。
• 第二步：在多阶段定价决策过程中考虑需求的不确定性以提升优化算法的鲁棒性：在MDP建模思路下，定义状态为库存数量，并假设真实销量服从以销量预估值为参数的泊松分布，从而得到状态转移概率，进而将时间序列定价优化问题转化为MDP模型，最后利用一个2阶段的动态规划方法进行复杂问题的求解。

技术亮点：
①在因果建模中使用参数模型解决技术挑战1中的价格稀疏性；
②在优化过程中考虑需求的不确定性，通过不确定建模解决技术挑战2中的预估不准确的问题；

1.2.2 折扣和销量之间的因果建模

总体ML建模思路：基础销量预估模型+价格弹性模型
为了解决商品历史价格稀疏（1-2个）的问题，会在因果模型中引入聚合类信息-商品品类信息Li（品类层级越高，sku个数越多，sku间的差异也越大），同时，借鉴文献[31]中的边际因果结构模型，提出一个半参数结构模型来学习单个商品的因果效应。公式中，Yi-nor 作为归一化因子，Yi/Yi-nor 表示折扣价和原价下的销量比值，采用比值而不是绝对值的原因是，比值能够规避“不同商品销量绝对值差异过大”的问题。

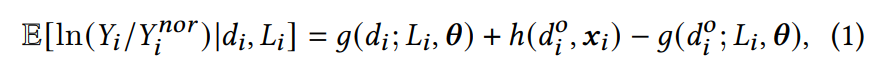
其中， ( ; , )是商品i的参数化价格弹性模型，增加可解释性，参数θ表示价格弹性向量，θ为所有商品所共享；

基础销量预估模型：
?( - ) 是无参数的ML预估模型，用于预估在近期平均折扣力度di下销量的对数比，模型选择不限，本文实验中选择的是XGB；

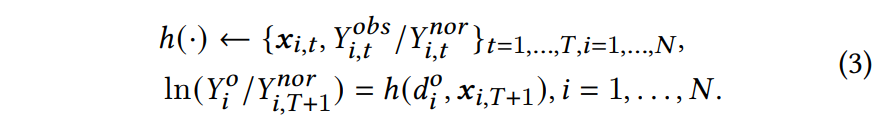
价格弹性模型：
构建一个双对数结构嵌套平均模型来预估用户对指定商品的平均价格敏感度。该模型会同时学习1~3级品类各自的弹性参数。

反事实预估：
将公式（3）和（4）带入（1）可以得到反事实销量预估公式，将[0,1]的折扣值带入即可，如下：

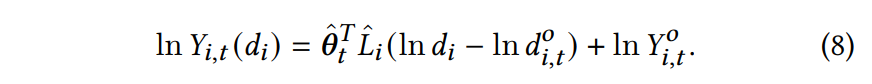
2 个人笔记：特定折扣下的反事实销量预测

2.1 核心式子1：整体方程结构

$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=g(d_i;L_i,\theta )+h(d_i^{\text{o}},x_i)?g(d_i^{\text{o}};L_i,\theta )$

函数$h(d_i^{\text{o}},x_i)$为非参数预测模型，用于预测某个商品平均折扣$d_i^{\text{o}}$下的销量，
如果$d_i=d_i^{\text{o}}$，那么
$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})|d_i^{\text{o}}]=h(d_i^{\text{o}},x_i)$
如果$d_i!=d_i^{\text{o}}$，那么$g(d_i)?g(d_i^{\text{o}})$代表的是，特别折扣下的增量（新折扣增量），所以通俗来说就是：
$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=平均折扣销(predict?model）+特殊折扣增量(price?elasticity)$

• $Y_i^{\text{o}}$是常规渠道产品$i$近期的平均销量
• $d_i^{\text{o}}$是商品$i$近期的平均折扣
• $Y_i/Y_i^{\text{nor}}$代表了折扣价格使得销量增加的百分比，因为不同商品销量差异很大，所以比率会比绝对值更有用
• 函数$g(d_i;L_i,\theta )$是参数化的价格弹性模型，参数$\theta \in {\mathbb{R}}^{m+1}$

2.2 核心式子2：销量预测模块

$\ln (Y_i/Y_{i,T+1}^{\text{nor}})=h(d_i^{\text{o}},x_{i,T+1}),i=1,...,N$

论文提到了，为什么不能直接使用
$E[\ln Y_i|do(d_i)]=h(d_i,x_i)$，把$treatment=d_i$ 当做一个特征和混杂因子$x_i$一起放入模型预测销量$\ln Y_i$？
贴一下原话，其实就是treatment=折扣 和 混杂因子也有强关联关系，所以除非你更新了折扣，也把关联的混杂因子也关联上，不然估计有偏。

Because transactional features, such as historical sales, are affected by the historical discount. If we do an intervention on the discount 𝑑𝑖 , i.e. varying the discount, we also need to change the relevant historical features 𝒙𝑖(𝑑𝑖) which is impossible.

同时为什么有$\ln (Y_i/Y_i^{\text{nor}})$是一种标准化的手法，消除不同商品之间销量的差异；
这里只用了$d_i^{\text{o}}$ 平均折扣，来计算平均折扣下的销量。

2.3 核心式子三：价格弹性

上面有提到，不同折扣会带动一系列混杂因子的改变以及销量的改变，这里借用价格弹性来还原，不同折扣下的销量变化情况。

其来自双log结构的nested模型

$g(d_i;L_i,\theta )=\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=({\theta }_1+{\theta }_2^{\mathsf{T}}{L}_i)\ln d_i+c$

将其转化为指数形态：

$Y_i=Y_i^{\text{nor}}{e}^c{d}_i^{{\theta }_1+{\theta }_2^{\mathsf{T}}{L}_i},?i$

其中，来解读一下这个式子，总销量 = 原价销量 * 销量变化量（价格弹性-折扣）：

• $Y_i$,商品i近几周总销量
• $Y_i^{\text{nor}}$,商品i近几周在无折扣原价下的平均销量
• ${\theta }_2\in {\mathbb{R}}^m$，$\theta =[{\theta }_1,{\theta }_2^{\mathsf{T}}{]}^{\mathsf{T}}$
• $c$为截距参数，这里是e的c次方亦然
• $L_i$为由三级one-hot变量组成，它是折扣的effect modifiers，而这个修饰器不仅由当个商品，还由所有category属性共同决定，算是一种global effect modifiers
  $L_i=[\underset{\text{category?1}}{0,?,1,0},\underset{\text{category?2}}{0,1,?,0},\underset{\text{category?3}}{0,?,0,1},{]}^{\mathsf{T}}$
• ${\theta }_1+{\theta }_2^{\mathsf{T}}{L}_i$就是价格弹性，所以每个独立SKU的价格弹性是由类别的价格弹性组成的。

2.4 反事实需求销量预测

假设我们获得了从时间1到时间$t?1$的观测数据，我们的目的：
预测不同折扣的产品𝑖 在时间𝑡时的反事实需求量。

将上面提到的核心式子2+3 带入式子1
式子2：$\ln (Y_i/Y_{i,T+1}^{\text{nor}})=h(d_i^{\text{o}},x_{i,T+1}),i=1,...,N$
式子3： $g(d_i;L_i,\theta )=\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=({\theta }_1+{\theta }_2^{\mathsf{T}}{L}_i)\ln d_i+c$
式子3的变形：
$Y_i=Y_i^{\text{nor}}{e}^c{d}_i^{{\theta }_1+{\theta }_2^{\mathsf{T}}{L}_i},?i$
.
带入半参模型式子1：
$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=g(d_i;L_i,\theta )+h(d_i^{\text{o}},x_i)?g(d_i^{\text{o}};L_i,\theta )$

可以得到最终的反事实需求预测模型为

$\ln Y_{i,t}(d_i)={\hat{\theta }}_t^{\mathsf{T}}{L}_i(\ln d_i?\ln d_{i,t}^{\mathsf{o}})+\ln Y_{i,t}^{\mathsf{o}}$

这里解决了【2.2 核心式子2：销量预测模块】提到的问题，可以自由改变折扣来进行销量预测。
不过这个式子，可以看做某商品：
$t时刻折扣下的销量=t时刻价格弹性系数?（某折扣?平均折扣）+无折扣下的销量$

2.5 动态优化（未完待续）

待续的是MDP部分，后面会单独沿着动态规划做学习，先放一下

基于反事实预估得到的销量不可避免存在一定的不确定性（ML中存在偏差和方差），为了提高优化算法的鲁棒性，需要将需求的不确定性考虑进去。基于MDP提出了一种多阶段联合价格优化方法。

$\begin{array}{rl}\underset{d_1,?,d_T}{\max }& \sum _{j\in \mathcal{J}}(\sum _{t=1}^{T_j}{p}_0{d}_t{Y}_{jt}(d_t)?w_j[B_j?\sum _{t=1}^{T_J}(Y_{jt}(d_t)+Z_{jt}){]}^{+})\\ \text{s.t.}& \sum _{t=1}^{T_j}(Y_{jt}(d_t)+Z_{jt})\le B_j?j\in \mathcal{J}\\ & l{b}_{jt}\le p_t\le u{b}_{jt}?t=1,\dots ,T_j,j\in \mathcal{J}\end{array}$

来解读一下：

• $w_j$是浪费损失的权重，$[?{]}^{+}$为非负运算符
• 商品价格为$p_0$，这个价格是常规渠道的销售价格，且价格固定，用$d_t$表示商品在周期$t$时的折扣，对应的价格为$p_t=p_0{d}_t$
• 通过，核心公式2，$\ln (Y_i/Y_{i,T+1}^{\text{nor}})=h(d_i^{\text{o}},x_{i,T+1}),i=1,...,N$，
  我们对于常规渠道的在平均折扣下的销量预测为$Z_{j,t}，?j,t$
• 反事实的销量预测为$Y_{jt}(d_t)$为利用最终需求公式：
  $\ln Y_{i,t}(d_i)={\hat{\theta }}_t^{\mathsf{T}}{L}_i(\ln d_i?\ln d_{i,t}^{\mathsf{o}})+\ln Y_{i,t}^{\mathsf{o}}$
• $l{b}_{jt}$和$u{b}_{jt}$是折扣最大和最小的上下限制
• $B_j$代表产品A库存量，这些将会在$Tj$天卖出,如果超过了这些天数，就会变质造成损失

对于上面这个问题，我们并不准备直接求解，考虑到可以打的折扣是是有限的，我们将这个问题转化成离散优化问题。
虽然模型已经给出了$Y_{jt}(d_t)$和$Z_{jt}$的预估，但是仍会有随机的误差，所以我们需要考虑上述问题的不确定性，我们用MDP来建模整个决策过程。
笔者来理解一下，目标函数的含义：
$折价后销量?价格?库存折损率?(总库存量?已销售量)$

到此笔者就没仔细往后看，因为涉及到MDP，可能是后面的功能，
看到这先给自己留下几个之前的问题：

• $Y_{jt}(d_t)$ 反事实销量预测中应该是涵盖了 $Z_{j,t}，?j,t$的预测部分？

2.6 实验对比

看实验对比，主要看他实操的时候有什么训练技巧

跟预测任务一样，评估模型的指标：RMAE，以当天的实际折扣来预测第二天降价渠道的销售

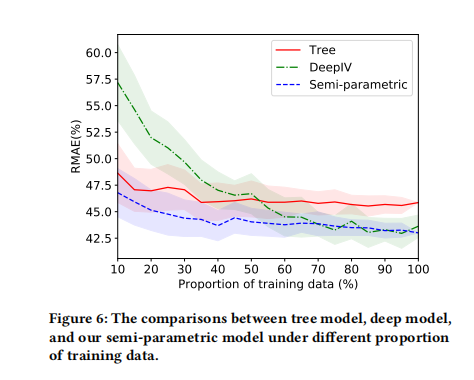
本模型是半参数模型，上图是顺着使用数据的比例增加三个模型的RMAE，
对比方案1-XGB：将折扣Treatment作为特征放入模型中预估销量值，但是这个模型本身存在混杂因子，估计是有偏的；
对比方案2-DeepIV：将三级品类的平均价格（treatment）作为工具变量，建模深度学习模型刻画折扣和销量的关系，其中折扣Treatment建模成高斯分布；

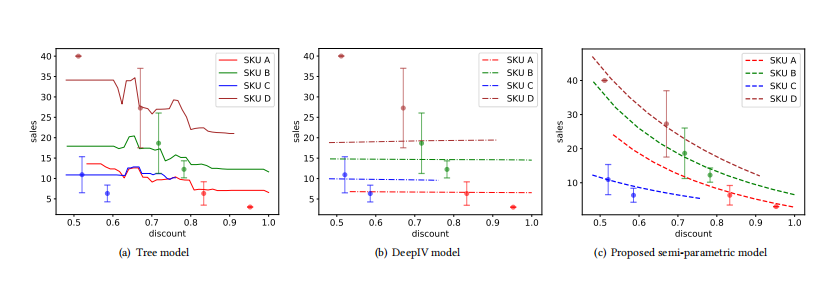
几个评价：

• 树形模型学习到的曲线具有不可预测的抖动，其结果在很大的折扣范围内保持不变（0.5-0.6,0.8-1.0）
• deepIV学习到的曲线几乎是一条线，这表明销售与价格无关。
  树模型和深度模型都不能正确地揭示价格-销售关系，推断的结果不可信。
• 半参数模型更加平滑，揭示了价格和销售之间的单调关系。收盘价之间的差异很小，这与直觉是一致的。

2.7 文章的一些启发

该文章有提到：

反事实预测和优化框架是相当通用的，可以应用于电子商务平台的其他场景：

• 在新鲜零售场景中，这种方法也可以应用于只有一天保质期的日新鲜商品的降价。
  它的目标是通过在一天结束前降价来促进销售，比如只剩下两个小时了。
• 在营销场景中，可以应用于个性化的优惠券分配任务，通过向有预算约束的不同用户分配不同的优惠券，来实现平台的整体投资回报(ROI)的最大化。
• 在客户服务场景中，可以应用于个性化补偿支付任务，通过为受预算约束的用户提供最优支付，从而最大化客户的满意度。

在上述三个例子中，处理分别为价格、优惠券和补偿支付，结果分别为产品销售、用户转化率和满意度，优化目标分别为总体利润、ROI和满意度。为了解决这些问题，我们首先基于半参数模型建立了治疗与结果之间的因果关系，然后利用预算或库存约束对目标进行优化。值得注意的是，我们在之前的工作中已经为第二种情况提出了一个营销预算分配框架

在营销场景中，该团队之前的一篇文章我也学习过，都是非常通用的营销预测框架类，很给力了：
预算分配Budget Allocation：两篇论文（二）

特征工程，四大类：

• 1 我们首先提取了产品和商店的特点。原始功能包括品牌、sku、部门、类别、周末、假日信息、销售渠道、促销活动、页面浏览量、用户浏览量、历史折扣和历史销售情况等。
• 2 我们使用数据聚合过程来创建新的特性。具体来说，我们汇总不同的时间段，如按周和假期，并汇总不同的集群，如品牌、类别、商店、sku、销售渠道。
• 3 第三，我们通过使用平均值或最近邻匹配来计算缺失的数据。其他方法也可以应用，如EM算法、插值和矩阵补全等。
• 4 对一级、二级、三级类别等稀疏特征进行了独热编码。