[人工智能]支持向量机

支持向量机(Support Vector Machine）

一、基本概念

1.超平面

超平面是指n维线性空间中的维度维n-1维的子空间，它可以把线性空间分割成两个不相交的部分。在二维空间中超平面是一条直线，三维空间中超平面是一个平面。n维空间中的超平面表示如下：
$${\omega }^{T}x+b=0$$其中${\omega }^T$和$x$都是n维列向量，$\omega$是平面上的法向量，决定了超平面的方向，b是一个实数代表的是超平面到原点的距离。

2.点到超平面的距离

对于一个超平面${\omega }^{T}x+b=0$，超平面上任意一点x’有${\omega }^T{x}^{\prime }+b=0$。空间中任意一点x到超平面上的距离等于xx’在法向量$\omega$上的投影：
$$d=|\frac{{\omega }^T}{||\omega ||}(x?x^{\prime })|$$
又因为${\omega }^T{x}^{\prime }=?b$，
$$d=\frac{{\omega }^{T}x+b}{||\omega ||}$$

3.判断超平面的正反

若${\omega }^T{x}_i+b>0$，x在超平面的正面；若${\omega }^T{x}_i+b<0$，x在超平面的反面。若${\omega }^T{x}_i+b=0$，x落在超平面上。 那么, 它的值正得越大, 代表点在平面的正向且与平面的距离越远. 反之, 它的值负得越大, 代表点在平面的反向且与平面的距离越远。

4.间隔与最大间隔

支持向量机(SVM)是一种判别分类的模型，在线性空间中使用决策边界来分离类，决策边界就是上面提到的超平面。在这路我们以二维空间为例子，利用超平面A将样本分成两类，我们称右边为正类，左边为负类。超平面A向左边平移首次碰到负类样本停止，得到边缘超平面A1，超平面A向右边平移首次碰到正类样本停止，得到边缘超平面A2。首次碰到边缘超平面的样本点称为支持向量。边缘超平面A1与边缘超平面A2之间的距离称为间隔。SVM目的是找到一个超平面将样本分类并且这个超平面到支持向量之间具有最大距离也就是使间隔最大化。

二、线性可分SVM

1.转化为二次规划问题

考虑一个包含n个训练实例的二分类问题，其中每个训练实例$x_i$与二元标签$y_i\in ?1,1$相关联。超平面由${\omega }^{T}x+b=0$表示，这意味着
$${\omega }^T{x}_i+b>0，y_i=1$$$${\omega }^T{x}_i+b<0，y_i=?1$$然后由点到超平面的公式
$$d=\frac{{\omega }^T{x}_i+b}{||\omega ||}$$
其中，|.|表示绝对值，||.||表示向量长度，令超平面与y=1的最近点的距离为$k_{+}>0$,令$k_{?}>0$表示超平面与负类最近点的距离。这个约束可以表示为：
$$\frac{{\omega }^T{x}_i+b}{||\omega ||}\ge k_{+},y_i=1$$
$$\frac{{\omega }^T{x}_i+b}{||\omega ||}\le k_{?},y_i=?1$$
可以通过$y_i和{\omega }^T{x}_i+b=0$的乘积来简洁表示
$$y_i({\omega }^T{x}_i+b)\ge M||w||$$
可以考虑以下优化问题：
$$\underset{w,b}{\max }M$$$$s.t.y_i({\omega }^T{x}_i+b)\ge M||w||$$
我们可以使用$||w||=\frac{1}{M}$来简化不等式的右边
$$\underset{w,b}{\max }\frac{2}{||w||}$$$$s.t.y_i({\omega }^T{x}_i+b)\ge 1$$
这里讲一下为什么化成$||w||=\frac{1}{M}$来简化不等式，对于超平面${\omega }^T{x}_i+b=0$等比例缩放w,b不会改变超平面，${\omega }^T{x}_i+b=0$缩放成$10{\omega }^T{x}_i+10b=0$，我们依然可以用${\omega }^{\prime T}{x}_i+b^{\prime }=0$来表示，只不过${\omega }^{\prime }=10w,b^{\prime }=10b$。在公式推导的过程中有$$\underset{w,b}{\max }\frac{{\gamma }_i}{||w||}$$$$s.t.y_i({\omega }^T{x}_i+b)\ge {\gamma }_i$$
在这里${\gamma }_i$是一个变量不是常量，如果我们能让三个变量的凸优化问题变成两个变量的凸优化问题，那么问题就会被简化，于是我们加上$s.t.{\gamma }_i=1$这个约束，为什么可以加上这个约束？
在这个式子$\gamma =y^{?}({\omega }^T{x}^{?}+b)$中(x* ，y*) 指那些支持向量，即那些支撑超平面的点。如果令$\gamma =1$，我们可以得到一组w,b再取$\gamma =10，100，1000，.....$，我们可以得到很多组解并且得到的w,b也大很多，但是描述的都是同一个超平面，所以我们不妨令$\gamma =1$得到一组相对“平凡”的w,b。
因此，SVM优化问题通常以下面形式表示，
$$\underset{w,b}{\min }\frac{||w||}{2}$$$$s.t.y_i({\omega }^T{x}_i+b)\ge 1$$
由于目标函数相对于$w$而言是二次凸函数，所以它被称为二次规划问题(QP, Quadratic Programming)

2.解二次规划

二次规划问题，可以采用解决约束规划问题的拉格朗日乘数法进行求解。

3.软边缘SVM

如图示，存在决策边界$B_1$和决策边界$B_2$，尽管$B_1$误分类样本，$B_2$正确分类了样本，但这并不表示$B_2$是比$B_1$好的决策边界。对于这个问题，我们要考虑如何修正SVM公式，利用一种称为软边缘(soft margin)的方法，学习允许一定训练错误的超平面。
为了在SVM公式中引入训练错误率的概念，让我们放松不等式约束以适应违反规定的少数实例，这样可以为每个训练$x_i$引入一个松弛变量${\xi }_i$来实现
$$y_i({\omega }^T{x}_i+b)\ge 1?{\xi }_i$$
变量${\xi }_i$允许在SVM中存在一些松弛，使得每个$x_i$不需要严格的满足$y_i({\omega }^T{x}_i+b)\ge 1$。
在存在松弛变量的情况下，重要的是要学习一个最大化间隔(确保良好的泛化性能)和最小化松弛变量(确保最低训练错误率)的超平面，这个可以通过优化问题来实现，如下所示：
$$\underset{w,b}{\min }\frac{||w||}{2}+C\sum _{i=1}^n{\xi }_i$$$$s.t.y_i({\omega }^T{x}_i+b)\ge 1?{\xi }_i$$$${\xi }_i\ge 0$$
其中$C$是一个超参数，在最大间隔和最小训练错误率之间做一个折中。求解松弛后的二次规划问题，可以应用拉格朗日乘子法将原始问题转换成相应的对偶问题进行求解。

三、线性不可分SVM

对于一些非线性可分的数据集，可以将原先的属性空间𝒙变换到一个新的空间𝜑(𝒙)（高维空间），在变换后的空间中使用原有的线性SVM方法来构造决策边界以实现数据集的二分类，然后可以将超平面投影回原始的属性空间，从而产生非线性决策边界——超曲面。
如下图的例子，通过变换空间实现了非线性决策边界的构造，其空间变换为: $\phi (x_i)=x_i^2?x_i，i=1,2$。

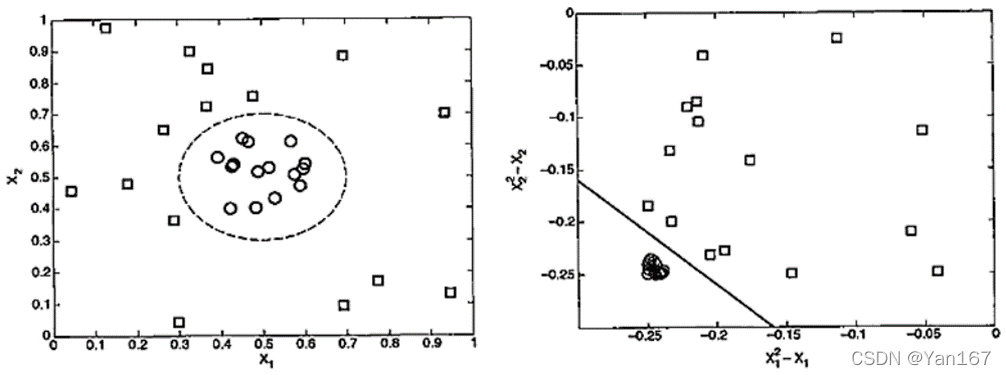
非线性SVM的计算推导过程也类似于前述的线性SVM，主要变化为：将计算过程中的${\mathbf{x}}_i$变为$\phi ({\mathbf{x}}_i)$。空间变换中，仅需使用𝜑(𝒙)的内积函数，这可以通过核技术来实现。使用核函数，可以直接在变换空间中处理内积，而不必处理非线性变换函数𝜑的确切形式，这意味使用高维变换的时候可以仅在原始属性空间中进行计算，不会引发维数灾难，且核函数计算内积也比变换后的𝜑(𝒙)要廉价得多，所以SVM在高复杂度和非线性问题中使用十分广泛。空间变换中使用的常用核函数有多项式核、径向基函数核以及S形核，其中径向基函数核（Radial Basis Function，RBF）是最常用的。
有关非线性SVM的计算以及核技术可参见《数据挖掘导论》（原著：《 Introduction to Data Mining 》，Pang-Ning Tan、Michael Stainbach，Vipin Kumar等著）等著作。

四、实验

1.调用库函数

from sklearn.svm import LinearSVC
from mglearn.datasets import make_blobs
import mglearn
import numpy as np
import matplotlib.pyplot as plt

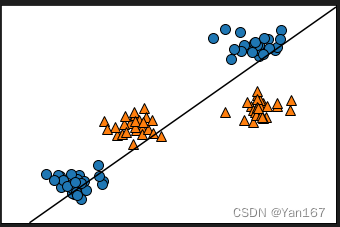
2.数据集线性不可分

#if dataset can not be devided by a linear model
X, y = make_blobs(centers=4, random_state=8)
y = y % 2

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

linear_svm = LinearSVC().fit(X, y)

mglearn.plots.plot_2d_separator(linear_svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

3.加入特征

# increase characters

X_new = np.hstack([X, X[:, 1:] ** 2])

from mpl_toolkits.mplot3d import Axes3D, axes3d

figure = plt.figure()

ax = Axes3D(figure, elev=-152, azim=-26)
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c= 'b', cmap=mglearn.cm2, s=60)
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c= 'r', cmap=mglearn.cm2, s=60)
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")

4.实验结果

对于线性不可分的数据，可以通过升维对其进行分类。在SVM中高维空间的操作等价于低维空间的操作，这也是为什么SVM能在高维空间中操作的原因。