在这个系列,我将会从零复习机器学习,以下为复习资料。
资料参考网上,如有侵权,删
算法讲解
一元线性回归中的一元指的是只有一个自变量
回归预测的问题是连续值

一元线性回归的目的:

要求解这个方程就需要确定两个参数
怎么求参数?
介绍一个概念叫做代价函数,也叫损失函数,是衡量真实值与预测值误差的一个函数。
一元线性回归代价函数如下
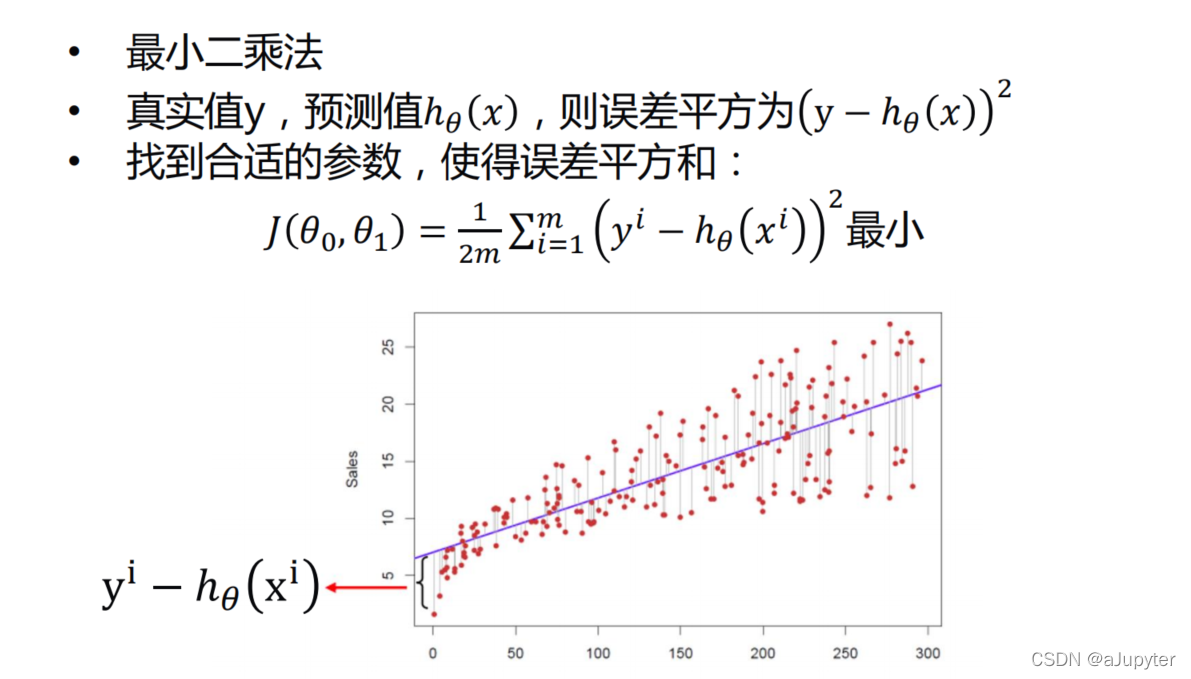
不用绝对值的原因是无法求导
介绍两个系数,了解即可
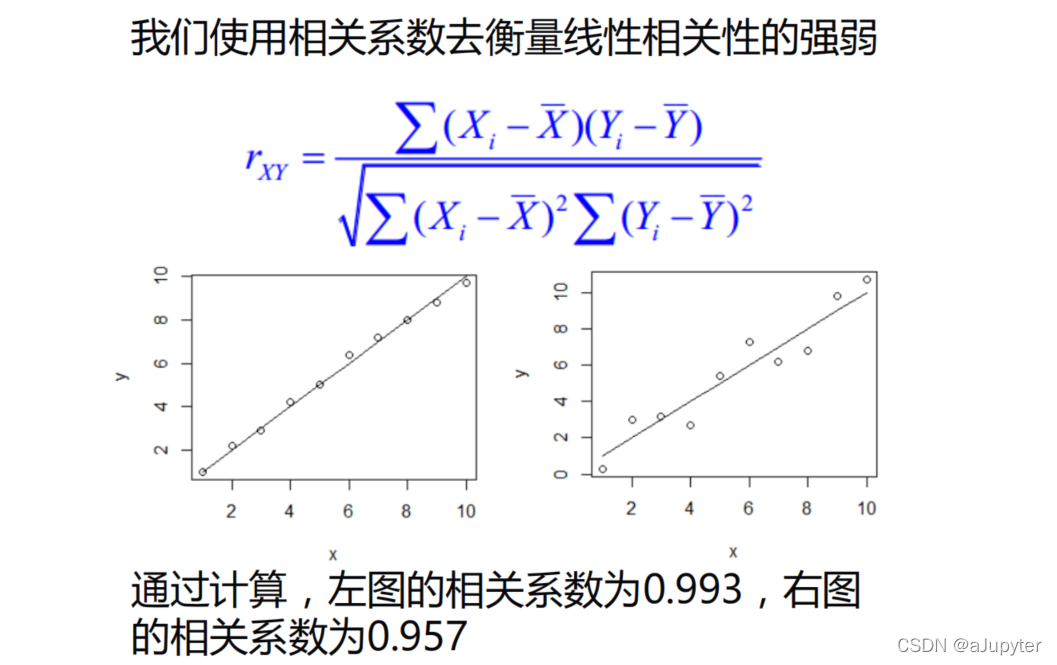

总目标是求两个参数,如何求?因为损失函数是两个参数的函数,所以只要这两个参数让损失函数值最小就是最优解,to put it another way,就是寻找让损失函数最小的参数。
怎么求?学过微积分的同学肯定就想到了求导,是的其实就是求导。但并不是一步求完,梯度是导数上升最大的方向,取负就是导数下降最大的方向。
我们称之为梯度下降算法

梯度的负方向就好比在下山,每进行一次,就是下一步山,终点就是山底
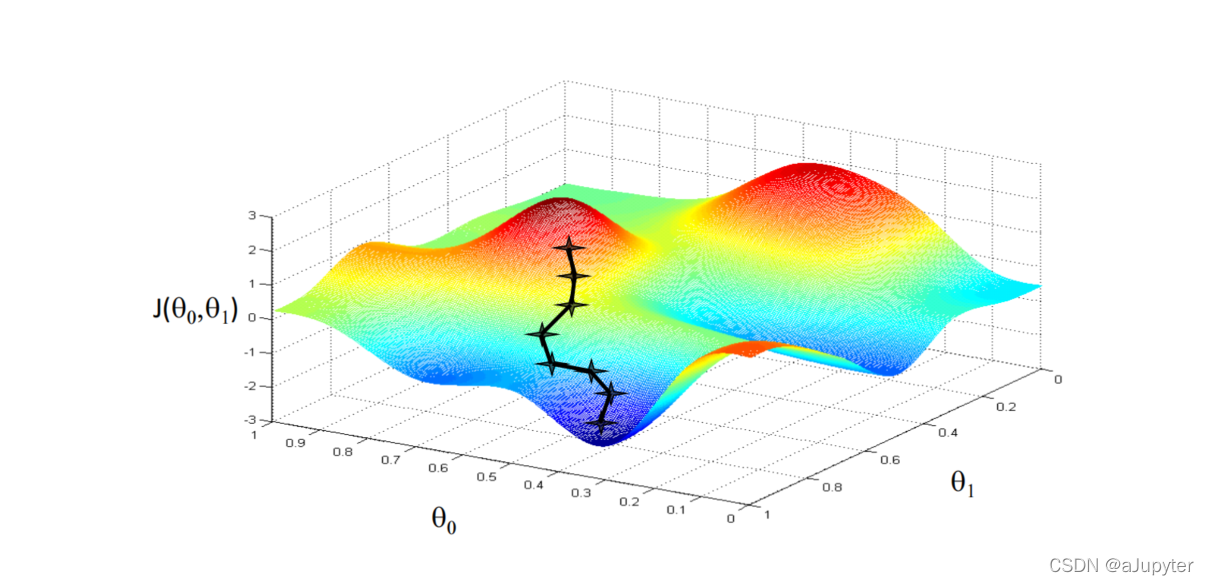
但需要注意的是要同步更新

学习率
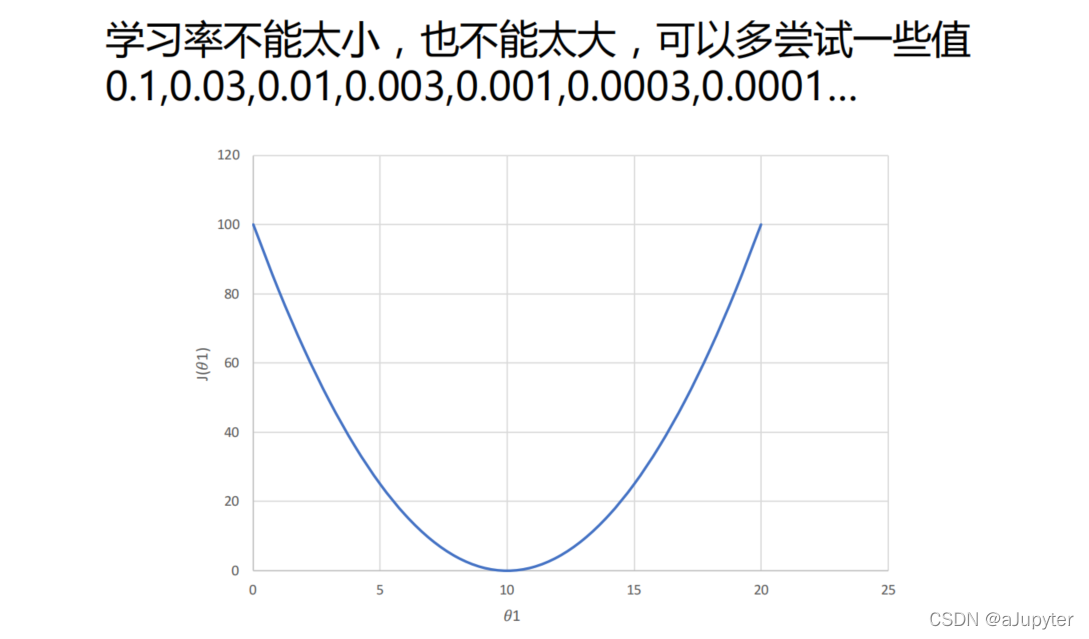
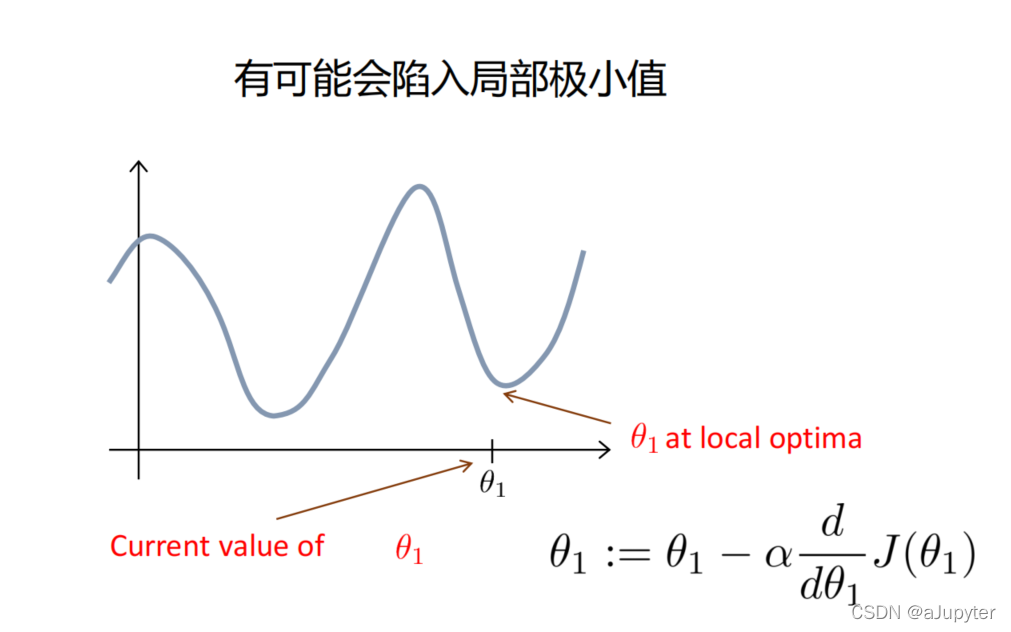
梯度下降算法的缺点就是容易陷入局部最小值(对于非凸函数,非凸函数可以理解为只有一个极小值)

化简

代码实现
# -*- coding: utf-8 -*-
"""一元线性回归及代码实现.ipynb
"""
import numpy as np
import matplotlib.pyplot as plt
"""# 一、数据集"""
# 读入数据集
data = np.genfromtxt('data.csv', delimiter=',')
'''
np.genfromtxt('data.csv', delimiter=',')
第一个参数是表格数组,可以简单理解为表格文件
第二个参数是文本之间的间隔符号
'''
print(data[:5]) #
x = data[:,0]
y = data[:,1]
print(x,y)
# 将数据可视化
plt.scatter(x,y) # 散点图
plt.show()
"""# 二、建模"""
# 最小二乘法
def compute_error(b, k, x_data, y_data):
totalError = 0
for i in range(0, len(x_data)):
totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
return totalError / float(len(x_data)) / 2.0
lr = 0.0001 # 学习率
# 最大迭代次数
epochs = 50
def gradident_descent(lr,epochs):
k = 0 # 斜率
b = 0 # 截距
for epoch in range(epochs):
# b_grad = 0
# k_grad = 0
# m = float(len(x))
# for j in range(0, len(x)):
# b_grad += (1/m) * (((k * x[j]) + b) - y[j])
# k_grad += (1/m) * x[j] * (((k * x[j]) + b) - y[j])
k_grad = (x*(k*x+b-y)).mean()
b_grad = (k*x+b-y).mean()
# 同步更新k和b,完成一次梯度下降算法
k -= lr * k_grad
b -= lr * b_grad
# 每迭代5次,输出一次图像
# if epoch % 5 == 0:
# print(f'epoch{epoch}')
# plt.plot(x,y,'b.') # b. 是指以蓝色的点显示
# plt.plot(x,k*x+b,'r')
# plt.show()
return k,b
print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x, y)))
print("Running...")
k,b = gradident_descent(lr,epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x, y)))
# 画图
plt.plot(x, y, 'b.')
plt.plot(x, k*x + b, 'r')
plt.show()
sklearn实现
"""# 三、skleran"""
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)
x_data = data[:,0,np.newaxis] # 因为sklearn要求输入的数据是二维
y_data = data[:,1,np.newaxis]
# 创建并拟合模型
model = LinearRegression()
model.fit(x_data, y_data)
# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()