机器学习线性回归分析
目的与要求
本文基于python语言,采用sklearn工具包进行线性回归实验。实验内容如下:
1,录入课本上关于房价预测的例程,并运行得出结果;
2,通过查找ptyhon编程资料,对给出的例程按要求进行修改,得出新的实验结果;
通过本实验应掌握如下内容:
1,训练样本与测试样本的随机选取;
2,通过sklearn工具包对数据进行线性回归拟合;
3,学会输出线性回归的统计量指标。
原理
实验一:本实验使用了sklearn中自带的波士顿房价的数据集进行预测。对数据进行了训练集与测试集的划分,训练集与测试集的比例为7:3.将训练集标准化后,运用ElasticNet函数进行模型的拟合,并将测试集代入模型进行预测,并对预测的结果进行评估。最后对验证集样本的预测值和真实值进行画图比较。因为训练样本的随机性选取,导致每次训练的模型并不完全相同,导致模型得分每次会有不同。为了减少误差,取五次的结果进行平均,以此来检验模型拟合的优劣。
实验二:本实验对数据集进行线性回归预测。原来代码中将数据的后二十个作为验证集,前面的作为测试集。这种主观的选取会对模型的训练带来影响。为了保证模型的可靠性,尝试对数据集进行随机划分。而原来验证集只含20个样本,样本数量偏少,在回归模型中我们一般选取数据集的1/5到1/4作为验证集,因此扩充验证集数量到90,以满足测试模型效果的目标。并画出相应的散点图和直线,从视觉上观察模型拟合的优劣。之后,增加特征变量,使特征变为二维,对模型进行训练,并画出相应的三维图。
实验代码:
#实验1
#1.波士顿房价数据
from sklearn.datasets import load_boston
boston = load_boston()
X = boston.data
y =boston.target
print(X.shape)
print(y.shape)
#2.划分数据集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7)#训练集占比为0.7
#3.数据标准化
from sklearn import preprocessing
standard_X = preprocessing.StandardScaler()
X_train = standard_X.fit_transform(X_train)
X_test = standard_X.transform(X_test)
standard_y = preprocessing.StandardScaler()
y_train = standard_y.fit_transform(y_train.reshape(-1, 1))
y_test = standard_y.transform(y_test.reshape(-1, 1))
# 4.运用ElasticNet回归模型训练和预测
from sklearn.linear_model import ElasticNet
ElasticNet_clf = ElasticNet(alpha=0.1, l1_ratio=0.71)
ElasticNet_clf.fit(X_train, y_train.ravel())
ElasticNet_clf_sorce = ElasticNet_clf.score(X_test, y_test.ravel())
print("lasso模式得分:", ElasticNet_clf_sorce)
print("特征权重:", ElasticNet_clf.coef_)
print("偏置值", ElasticNet_clf.intercept_)
print("迭代次数", ElasticNet_clf.n_iter_)
#5.画图
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(20, 3))
axes = fig.add_subplot(1, 1, 1)
line1, = axes.plot(range(len(y_test)), y_test, 'b', label='Actual_Value')
ElasticNet_clf_result = ElasticNet_clf.predict(X_test)
line2, = axes.plot(range(len(ElasticNet_clf_result)), ElasticNet_clf_result, 'r--', label='ElasticNet_Predict')
axes.grid()
fig.tight_layout()
plt.legend(handles=[line1, line2])
plt.title('ElasticNet')
plt.show()
#实验二:
#单一特征值:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 3]
# Split the data into training/testing setindes
index = np.random.randint(0,len(diabetes_y),90)
diabetes_X_train = np.delete(diabetes_X,index,0)
diabetes_X_test = [diabetes_X[i] for i in index]
#diabetes_X_train = diabetes_X[:-20]
#diabetes_X_test = diabetes_X[-20:]
# Split the targets into training/testing sets
diabetes_y_train = np.delete(diabetes_y,index,0)
diabetes_y_test = [diabetes_y[i] for i in index]
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
print("Coefficients: \n", regr.coef_)
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
#两个特征值:
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
ax = plt.axes(projection='3d')
fig = plt.figure()
# Load the diabetes dataset
diabetes_X, diabetes_z = datasets.load_diabetes(return_X_y=True)
# Use only one feature
diabetes_y = diabetes_X[:, np.newaxis, 2]
diabetes_X = diabetes_X[:, np.newaxis, 3]
diabetes=np.hstack((diabetes_X,diabetes_y))
# Split the data into training/testing setindes
index = np.random.randint(0,len(diabetes_z),80)
diabetes_train = np.delete(diabetes,index,0)
diabetes_test = np.array([diabetes[i] for i in index])
#diabetes_X_train = diabetes_X[:-20]
#diabetes_X_test = diabetes_X[-20:]
# Split the targets into training/testing sets
diabetes_z_train = np.delete(diabetes_z,index,0)
diabetes_z_test = [diabetes_z[i] for i in index]
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_train, diabetes_z_train)
# Make predictions using the testing set
diabetes_z_pred = regr.predict(diabetes_test)
# The coefficients
print("Coefficients: \n", regr.coef_)
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(diabetes_z_test, diabetes_z_pred))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(diabetes_z_test, diabetes_z_pred))
# Plot outputs
diabetes_z_test=np.array(diabetes_z_test)
ax.scatter3D(diabetes_test[:,0],diabetes_test[:,1], diabetes_z_test, c=diabetes_z_test)
ax.plot_trisurf(diabetes_test[:,0],diabetes_test[:,1], diabetes_z_pred)
ax.view_init(20, 25)
plt.show()
运行结果:
实验一:


实验二:
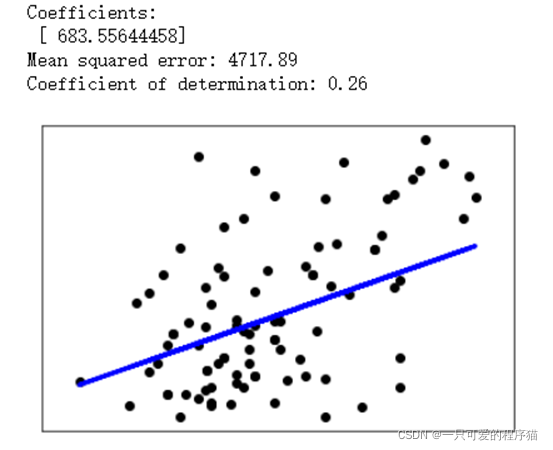
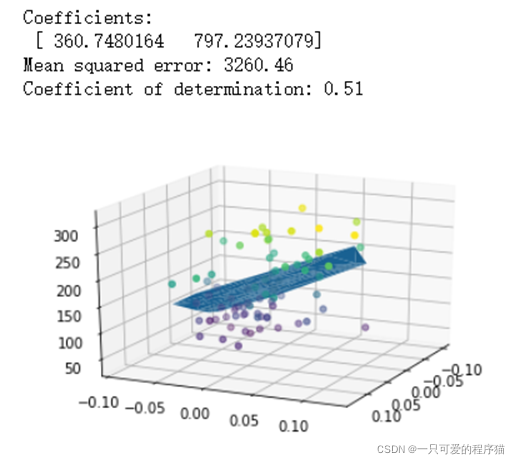
问题与分析:
在取数据时,利用切片所得的是一维数组,与后续训练时所需的数据格式不匹配,在切片时,要加上np.newaxis新建一个维度,得到n1的二维数组。在随机选取验证集时,可以调用numpy的random.randint函数。作三维图时,要从mpl_toolkits 里导入 mplot3d,在画图时要注意输入的格式。用np.hstack将所取的第三个和第四个特征值合并成一个n2的二维数组,来进行模型的预测。