[人工智能]一元线性回归(sklearn)

1.手工梯度下降法

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

#载入数据
data=np.genfromtxt("/root/jupyter_projects/data/fangjia1.csv",delimiter=',')
#x_data=data[0:,0]#分离data数据，取所有行第0列 
x_data=data[:,0]#等价于上边那行
y_data=data[:,1]
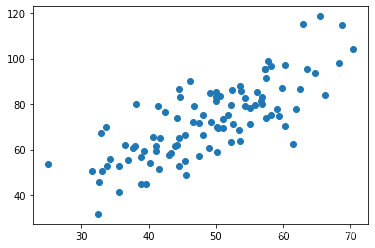
plt.scatter(x_data,y_data)#绘制散点图
plt.show()

#学习率learning rate
lr=0.0001
#截距
theta_0=0
#斜率
theta_1=0
#最大迭代次数
epochs=50

$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\sum }_{i=1}^m(\widehat{(}{y}^{(i)})?y^{(i)}{)}^2=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{{}^{(i)}})?y^{(i)}{)}^2$

#最小二乘法
#计算代价函数
def compute_error(theta_0,theta_1,x_data,y_data):
    totalError=0
    for i in range(0,len(x_data)):
        totalError+=(theta_1*x_data[i]+theta_0-y_data[i])**2
    totalError
    return totalError/float(2*len(x_data))

对代价函数求偏导：
$\frac{?}{?{\theta }_j}J({\theta }_0,{\theta }_1)=\frac{?}{?{\theta }_j}\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})?y^{(i)}{)}^2$

${\theta }_0:j=0$:$\frac{?}{?{\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})?y^{(i)})$

${\theta }_1:j=1$:$\frac{?}{?{\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})?y^{(i)})?x^{(i)}$

应用梯度下降法修改不断当前值

${\theta }_0$=${\theta }_0?\alpha ?\frac{?}{?{\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})?y^{(i)})$

${\theta }_1$=${\theta }_1?\alpha ?\frac{?}{?{\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})?y^{(i)})?x^{(i)}$

#梯度下降
def gradient_descent_runner(x_data,y_data,theta_0,theta_1,lr,epochs):
    m=len(x_data)
    #达到最大迭代次数后停止
    for i in range(epochs):
        theta_0_grad=0
        theta_1_grad=0#求梯度该变量
        for j in range(0,len(x_data)):
            theta_0_grad+=(1/m)*((theta_1*x_data[j]+theta_0)-y_data[j])
            theta_1_grad+=(1/m)*((theta_1*x_data[j]+theta_0)-y_data[j])*x_data[j]
        theta_0=theta_0-(theta_0_grad*lr)#同时更新参数模型
        theta_1=theta_1-(theta_1_grad*lr)

        #没迭代5次更新一次图像
        if i%5==0:
            print("epochs:",i)
            plt.scatter(x_data,y_data)
            plt.plot(x_data,theta_1*x_data+theta_0,'r')
            plt.show()
    return theta_0,theta_1
        

print("starting theta_0={0},theta_1={1},error={2}".format(theta_0,theta_1,compute_error(theta_0,theta_1,x_data,y_data)))
print('running')
theta_0,theta_1=gradient_descent_runner(x_data,y_data,theta_0,theta_1,lr,epochs)
print("end{0} theta_0={1},theta_1={2},error={3}".format(epochs,theta_0,theta_1,compute_error(theta_0,theta_1,x_data,y_data)))


#画图
# plt.scatter(x_data,y_data)
# plt.plot(x_data,theta_1*x_data+theta_0,'r')
# plt.show()

starting theta_0=0,theta_1=0,error=2782.5539172416056
running
epochs: 0

epochs: 10

epochs: 20

epochs: 30

epochs: 40

epochs: 45

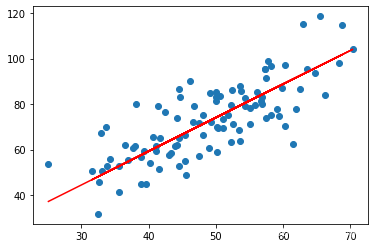
end50 theta_0=0.030569950649287983,theta_1=1.4788903781318357,error=56.32488184238028

2.sklearn实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
%matplotlib inline

#载入数据
data=np.genfromtxt("/root/jupyter_projects/data/fangjia1.csv",delimiter=',')
#x_data=data[0:,0]#分离data数据，取所有行第0列 
x_data=data[:,0]#等价于上边那行
y_data=data[:,1]
plt.scatter(x_data,y_data)#绘制散点图
plt.show()
print(x_data.shape)
#x_data

(100,)

x_data=data[:,0,np.newaxis]
print(x_data.shape)#将x_data 转换为一个矩阵
y_data=data[:,1,np.newaxis]
#x_data

(100, 1)

#创建并拟合模型
model=LinearRegression()
theta=model.fit(x_data,y_data)

#画图
plt.scatter(x_data,y_data)
plt.plot(x_data,model.predict(x_data),'r')
plt.show()
print(theta)
print(model.coef_)#theta_0
print(model.intercept_)#theta_1
```![请添加图片描述](https://img-blog.csdnimg.cn/0b20585b7b97402a8930dfce71636c0f.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5piv5b-Y55Sf5ZWK,size_12,color_FFFFFF,t_70,g_se,x_16)