[人工智能]机器学习三 归一化_正则化_多项式升维

一. 归一化

1.归一化的目的

把数据变为（0，1）之间的数 ,使得在梯度下降的过程中，不同维度的θ值（或w）参数可以在接近的调整幅度上。保持数据在迭代过程中的θ值幅度基本一致。

2.常用的归一化类别

最大值最小值归一化

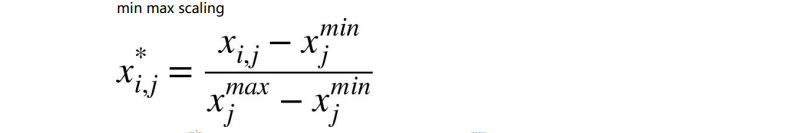
参数解释：
Xj min: X 矩阵中第 j 列特征值的最小值，
Xj max: X 矩阵中第 j 列特征值的最大值，
Xij : X 矩阵中第 i 行第 j 列的数值，
X*i,j : 归一化之后的 X 矩阵中第 i 行第 j列的数值。

标准归一化
包含了均值归一化和方差归一化。经过处理的数据符合标准正态分布，即均值为 0，标准差为 1

3. 两种归一化的优缺点

最大值最小值归一化
优点：一定可以把数值归一到 0到 1 之间，
缺点：如果有一个离群值，会使得一个数值为 1，其它数值都几乎为 0，受离群值的影响较大。
标准归一化
优点：不受离群值影响，因素标准归一化除以的是标准差，标准差的计算和所有数据样本有关。
缺点：不一定归一在0到1之间

二. 正则化

1. 过拟合和欠拟合

under fit：欠拟合，训练集和测试集的准确率都还没有到达最高。学的还不到位。
over fit： 过拟合，训练集的准确率升高的同时，测试集的准确率反而降低。
正则化就是防止过拟合，增加模型的鲁棒性 robust或者泛化能力。常用的正则惩罚项有 L1 正则项或L2 。其中，L1和L2正则的公式，在数学里意义就是范数，代表空间中向量到原点的距离

2. 岭回归(Ridge)和拉索回归(Lasso)

当我们把多元线性回归损失函数加上 L2 正则的时候，就是 Ridge 岭回归,
当我们把多元线性回归损失函数加上 L1 正则的时候，就是 Lasso 回归。
当我们把多元线性回归损失函数加上 L1和L2正则项，就是 Elasiticnet回归

从上图可知，L1的正则项通常会使得计算模型有的θ趋近于0，有的θ值很大。而 L2 会使得 θ 参数整体变小。如果从梯度下降的角度解释，损失函数MSE加上正则项，那么求导函数就等于多了正则项的导函数，即 MSE的导函数和 L1、L2 的导函数，那么梯度 gradient 就由两部分组成：学习率η×(MSE的导+L1/L2的导)。比不加惩罚项要多更新一部分，这部分就使得 θ趋近于原点 0 。

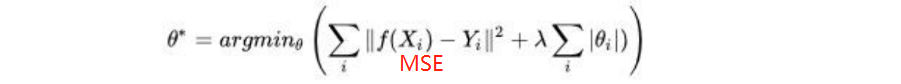
既然现在要去最小化的整体损失函数变成了两部分加和那么θ就既得满足原有的损失函数比如 MSE，同时还得满足 L1 或者 L2 这部分，从图上来说就是θ得在紫色的损失函数等高线上同时又得在红色的 L1 或 L2 的等高线上，说白了就是要出现在交点上面。

3. 代码实现岭回归(Ridge)和拉索回归(Lasso)

import numpy as np
from sklearn.linear_model import Ridge
from sklearn.linear_model import SGDRegressor


# 公式：all_loss = mse + l2
# all_loss = 1/2* sum((xiw -yi)**2 + (wi)**2) + sum((wi)**2)
#          = ||xw - y||2**2 + ||w||2**2			

# 创建数据
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# alpha就是公式中的lamda=0.4 
#solver=’sag’就是使用随机梯度下降法来求解最优解
ridge_reg = Ridge(alpha=0.4, solver='sag')
ridge_reg.fit(X, y)

#第二种方法
sgd_reg = SGDRegressor(penalty='l2', max_iter=1000)
sgd_reg.fit(X, y.ravel()) #y要求行向量

print(sgd_reg.predict([[1.5]]))
print("W0=", sgd_reg.intercept_)
print("W1=", sgd_reg.coef_)

import numpy as np
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor

# 公式：all_loss = mse + l1
# all_loss = 1/2* sum((xiw -yi)**2 + (wi)**2) + sum((wi))
#          = ||xw - y||2**2 + ||w||1			

# 创建数据集
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 第一种方法
lasso_reg = Lasso(alpha=0.15, max_iter=30000)
lasso_reg.fit(X, y)
print(lasso_reg.predict(1.5))
print(lasso_reg.intercept_)
print(lasso_reg.coef_)

# 第二种方法
sgd_reg = SGDRegressor(penalty='l1', max_iter=10000)
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))
print(sgd_reg.intercept_)
print(sgd_reg.coef_)

4. Elasiticnet回归

elasiticnet回归既有L1正则项，又有L2正则项，公式如下：0< p <1,如果p越大,L1越大，p越小L2越大，α越大模型泛化能力越强，a越小，模型精确度越高

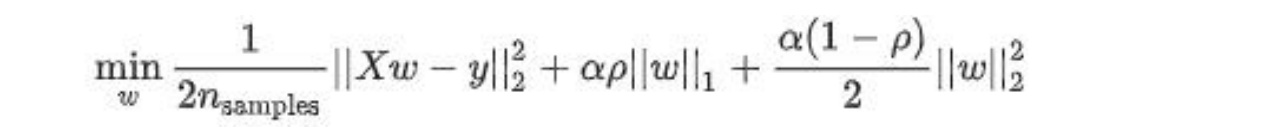
import numpy as np
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import SGDRegressor

# 创建数据集
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 构建模型
# alpha 经验值为4
# l1_ratio就是上公式中的p
elastic_net = ElasticNet(alpha=0.4, l1_ratio=0.15) 
elastic_net.fit(X, y)
print(elastic_net.predict(1.5))

# 第二种方法
# penalty='elasticnet' 表示公式采用L1和L2
sgd_reg = SGDRegressor(penalty='elasticnet', max_iter=1000)
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))

三. 多项式升维

1. 多项式升维的目的

多项式升维（或叫多项式回归）的目的是为了解决欠拟合，是数据处理阶段，非多元线性回归。多项式回归是为了扩展线性回归算法来适应更广泛的数据集。
例如：y_hat = w0 + w1*x1 +w2*x2 如果用二阶多项式升维x1,x2就会扩展成x1,x2, x1平方, x2平方,x1*x2，公式y_hat = w0 + w1*x1 +w1*x2 +w3*x1**2 +w4*x2**2 +w5*x1x2

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error


np.random.seed(42)
m = 100 # 样本数
X = 6 * np.random.rand(m, 1) - 3 # -3~3之间的数
y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1)

X_train = X[:80]
y_train = y[:80]
X_test = X[80:]
y_test = y[80:]

# 把真实数据的点画在二维平面中
plt.plot(X, y, 'b.')

# 构建一阶，二阶，十阶多项式回归字典
degree_dict = {1: 'g-', 2: 'r+', 10: 'y*'}
for i in degree_dict:
	poly = PolynomialFeatures(degree=i, include_bias=True) # degree 阶数 include_bias 截距项
	X_poly_train = poly_features.fit_transform(X_train)
	X_poly_test = poly_features.fit_transform(X_test)
	
	# 训练模型
	line_reg = LinearRegression(fit_intercept=False) # 取消截距项
	line_reg.fit(x_poly_train,y_train)
	
	# 预测
	y_train_predict= line_reg.predict(x_poly_train)
	y_test_predict= line_reg.predict(x_poly_test)
		
	#画图
	plt.plot(x_poly_train[:,1],y_train_predict, degree[i]) # 只能有一个维度
	
	# metrics
	print(mean_squared_error(y_train,y_train_prdict)
	print(mean_squared_error(y_test,y_test_prdict)
plt.show()