[人工智能]吴恩达机器学习笔记(一、二）

机器学习的定义

什么是机器学习？
机器学习（Machine Learning）：是研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。一个程序被认为能从经验E中学习，解决任务 T，达到性能度量值P，当且仅当，有了经验E后，经过P评判， 程序在处理T时的性能有所提升。

监督学习

监督学习（Supervised Learning）：对于数据集中每一个样本都有对应的标签，包括回归（regression）和分类（classification）；
若我们欲预测的是离散值，例如：“好瓜” “坏瓜”，此类学习任务成为“分类”（classification）；
若欲预测的是连续值，例如西瓜成熟度0.95、0.37，此类学习任务成为“回归”（regression）。
对只涉及两个类别的“二分类”（binary classification)任务，通常称其中一个为“正类”（postive class),另一个为“反类”（negative class)。
一般地，预测任务是希望通过对训练集{（x1,y1),(x2,y2),…，（xm,ym}进行学习，建立一个从输入空间x到输出空间y的映射f:x->y。对二分类任务，通常令γ={-1，+1}或{0，1};对多分类任务，|γ|>2;对回归任务，γ=R，R为实数集。

无监督学习

无监督学习（Unsupervised Learning）：数据集中没有任何的标签，包括聚类（clustering）。
聚类（clustering），即将训练集中的西瓜分成若干组，每组称为一个“簇”（cluster）,例如“浅色瓜”“深色瓜”，“本地瓜”“外地瓜”。

模型描述

模型描述（model representation）
线性回归模型：

给定训练样本 (xi，yi)其中： i = 1 , 2 , . . . , m, i=1,2,…,m i=1,2,…,m， 表示特征， y 表示输出目标，监督学习算法的工作方式如图所示：

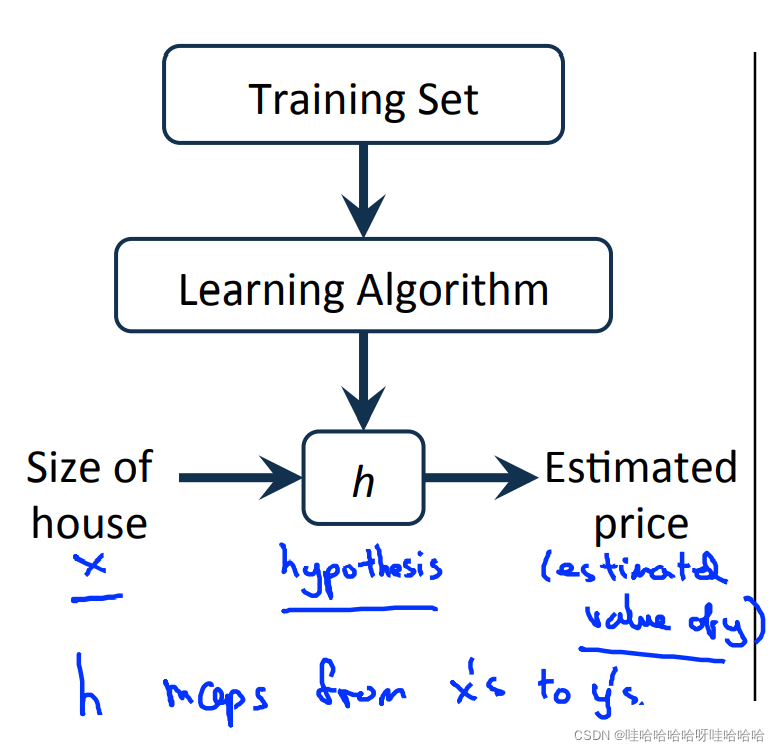
假设函数h(hypothesis)：是一个从输入 x到输出 y的映射，假设函数h(hypothesis)：${\theta }_0$和 ${\theta }_1$ ?都是模型参数。

代价函数

代价函数（cost function）$J(\theta )$，通常使用平方误差函数，如下：
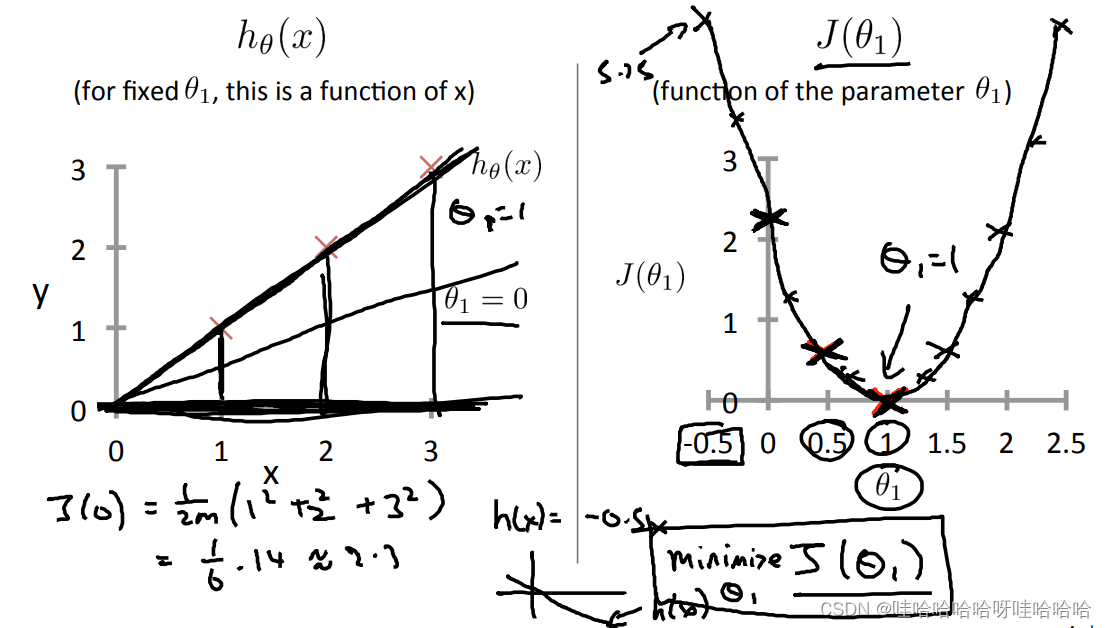
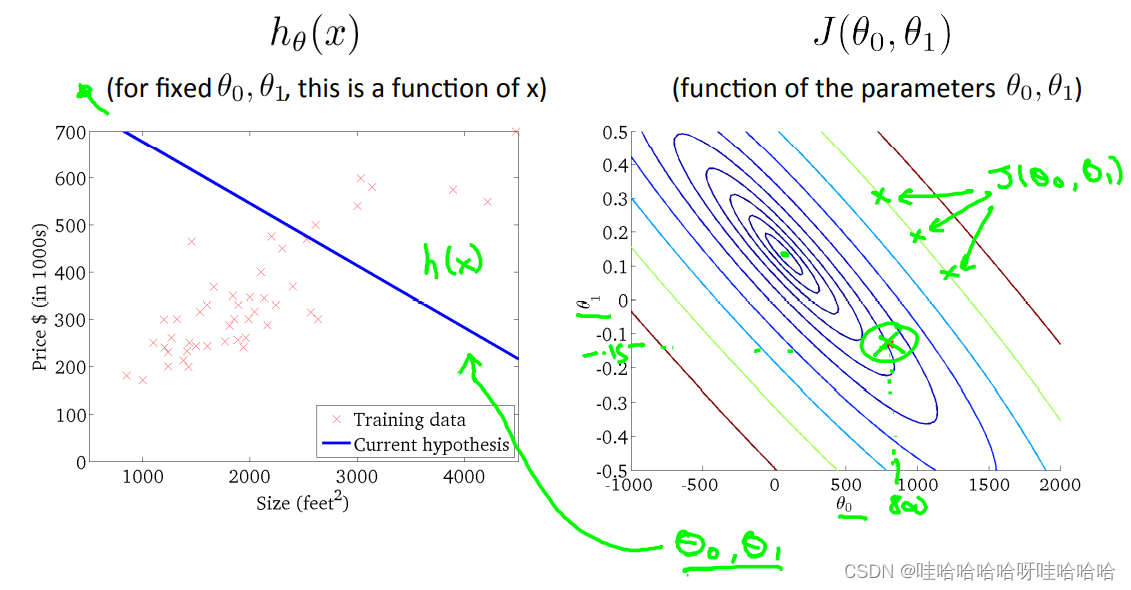
$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h(x^i)?y^i{)}^2$$m为训练样本的数量。训练的目标为最小化代价函数，即 $$\underset{{\theta }_0,{\theta }_1}{\mathrm{minmize}}J({\theta }_0,{\theta }_1)$$

梯度下降

梯度下降（gradient descent)可将代价函数J最小化。
代价函数：$J({\theta }_0,{\theta }_1)$，可以推广到 $J({\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n)$
目标：$$\underset{{\theta }_0,{\theta }_1}{\min }J({\theta }_0,{\theta }_1)$$
初始化 ${\theta }_0,{\theta }_1$?，
更新公式：$${\theta }_j={\theta }_j?\alpha \frac{?}{?{\theta }_j}J({\theta }_0,{\theta }_1)$$ α为学习速率（learning rate）。

同步更新（simultaneous update)${\theta }_0,{\theta }_1$

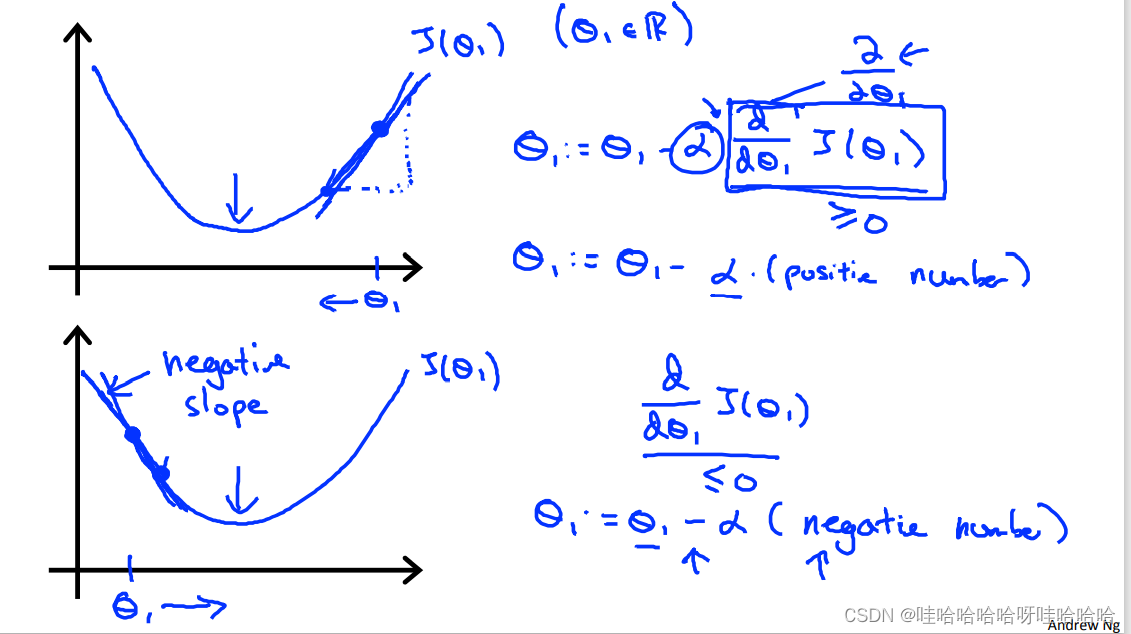
梯度下降总结：
1）如果α太小，梯度下降会变得缓慢；如果α太大，梯度下降可能无法收敛甚至发散。
2）当接近局部最小值时，梯度下降将自动采取较小的步。所以，不需要减小α。
3）梯度下降可以收敛到局部最小，即使学习速度是固定的。

线性回归的梯度下降

update ${\theta }_0,{\theta }_1$ ?simultaneously

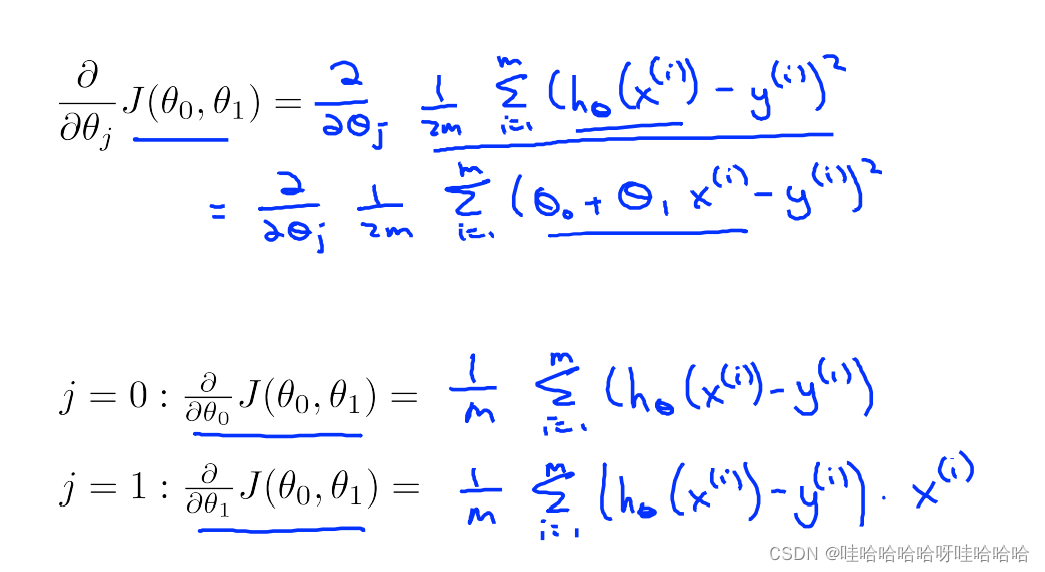
梯度下降的每一步遍历的所有数据集中的样例，又叫“batch” Gradient Descent Algorithm。
借鉴
原文链接：https://blog.csdn.net/qq_29317617/article/details/86312154