Merton模型的参数校准与定价
代码基于python平台实现,全部代码获取地址如下:
https://download.csdn.net/download/xiaowu1997/74783744
前言
1973 年,美国的数学家、经济学家 Black 和Scholes提出了一个较为完整的期权定价模型,称为 Balck-Scholes 模型。Balck-Scholes 模型是较为理想的欧式期权定价模型,模型的提出为期权的发展奠定了基础,在理论和实践方面都有着重大的意义。由于 Balck-Scholes 模型的是在标的资产的价格服从正态分布以及常数波动率等假设上建立起来的,这些假设与实际交易市场的数据表现出矛盾之处:常数波动率无法解释期权的隐含波动率微笑现象,并且标的资产的价格服从正态分布也与实际市场的标的资产呈现尖峰厚尾且倾斜的现象不符。
由于 Balck-Scholes 模型在假设方面的不足,因此后续的学者不断对 Balck-Scholes 模型进行了修正和改进。1973 年,Merton在 BS 模型的基础上引入了跳跃扩散过程,该模型通过将跳跃扩散参数与泊松过程相加来模拟资产价格的波动。
一、Merton模型
Merton 模型假设标的资产价格的变化路径服从跳跃扩散过程。其中,标的资产的价格变化过程中的跳跃部分属于可分散风险,具有系统性风险的标的资产价格变化用几何布朗运动描述,非系统性风险的标的资产价格跳跃用泊松跳跃过程描述,跳跃的幅度则用正态分布表示。
引入跳跃扩散过程后,标的资产价格服从如下方程
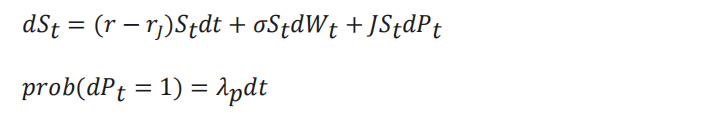
其中,𝑞是连续股息收益率,𝑊𝑡是标准布朗运动,𝑃𝑡为强度𝜆的泊松过程,𝑟𝐽为跳跃的漂移修正项,且:
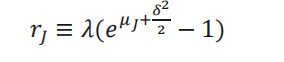
𝜇𝐽是 J 的均值,𝐽表示跳跃,并且其分布满足:
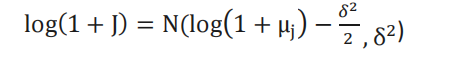
在风险中性估值的假设条件下,看涨期权的价值就等于未来预期价值按照无风险利率折现之后的现值,即:
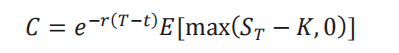
按照跳跃的次数以及所有可能的扩散路径对𝑆𝑇进行分组,可以得到所有𝑆𝑇的值,因此有:
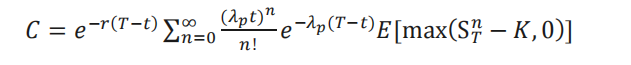
其中,S𝑇𝑛为经历 n 次跳跃及其后的扩散过程之后,标的资产价格在到期日的对数正态分布。
用 Black-Scholes 期权模型的价格表示式 中的期望值,则有:
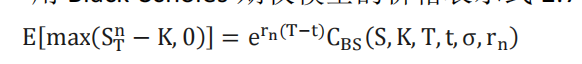
其中,𝐶𝐵𝑆(𝑆, 𝐾, 𝑇,𝑡, 𝜎, 𝑟𝑛)表示标准 Black-Scholes 期权定价公式下的看涨期权价格,𝑟𝑛满足:
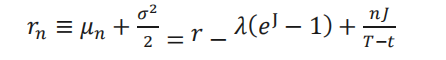
其中,𝜇𝑛为标的资产在发生 n 次跳跃之后的回报率,表达式为:
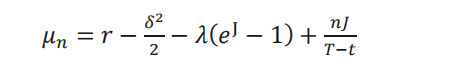
将式 联立,可以得到:
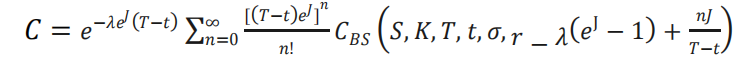
上式 为一个混合公式,可以求欧式看涨期权在跳跃扩散模型下的价格,将式 2.13 右侧的𝐶𝐵𝑆换成𝑃𝐵𝑆,即 Black-Scholes 期权定价中的看跌期权价格,各项参数保持不变,可求得欧式看跌期权在跳跃扩散模型下的价格。
二、Merton模型的三种定价方法
利用傅里叶方法,可以得到Merton模型的半解析解的形式,在给定模型的欧式看涨期权时,可以知道Merton模型的特征函数

三种定价方法:
①数值积分
②快速傅里叶变换
③蒙特卡洛模拟
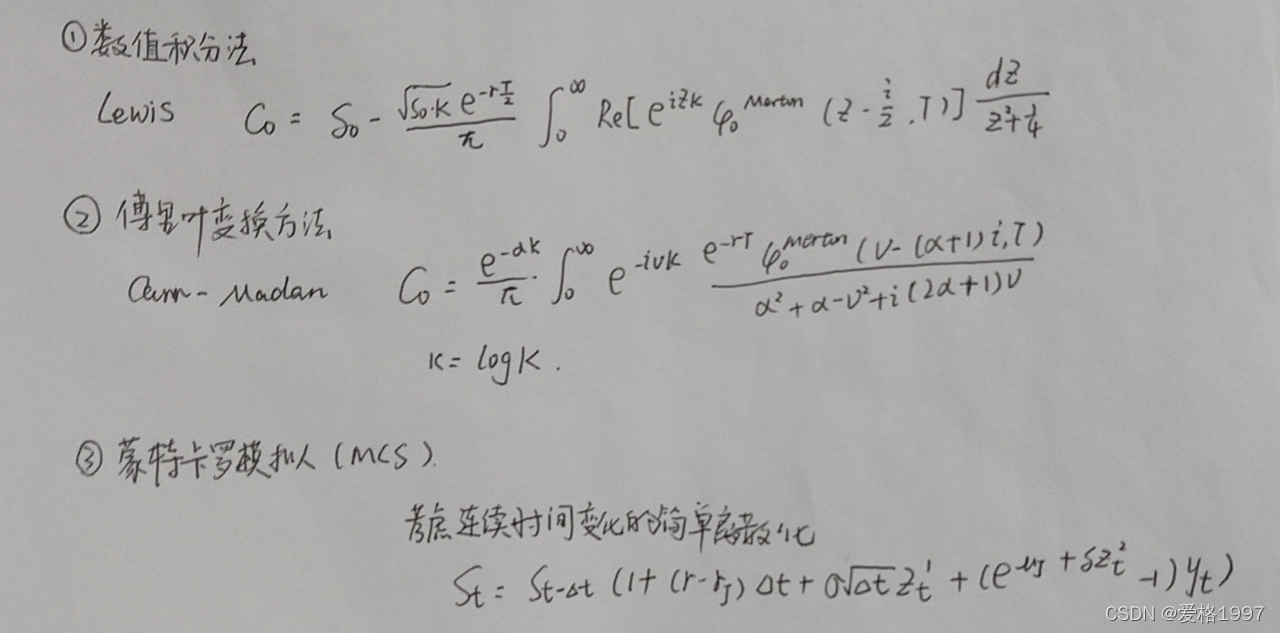
三、Merton模型的校准
为了使Merton模型最高程度的复制观测到的期权市场报价,需要定义一个误差函数来校准模型的四个参数,使用均方根误差函数(RMSE)进行校准

需要校准的参数为:
sigma, lamb, mu, delta
四、Merton模型的三种方法定价对比
通过上文的介绍,我们使用数值积分、快速傅里叶变化、蒙特卡洛模拟三种方法对Merton模型进行定价。
这里展示部分代码:
# Merton76模型在BSM模型中的几何布朗运动中增加了跳跃因素
# Merton跳跃扩散模型 通过数值积分求解/Lewis
# Valuation of European Call Options
# in Merton's (1976) Jump Diffusion Model
# via Numerical Integration
import math
import numpy as np
from scipy.integrate import quad
#
# Model Parameters
#
S0 = 100.0 # initial index level
K = 100.0 # strike level
T = 1.0 # call option maturity
r = 0.05 # constant short rate
sigma = 0.4 # constant volatility of diffusion
lamb = 1.0 # jump frequency p.a.
mu = -0.2 # expected jump size
delta = 0.1 # jump size volatility
print("Value of Call Option %8.3f"
% M76_value_call_INT(S0, K, T, r, sigma, lamb, mu, delta))
Value of Call Option 19.948
print("Value of Call Option %8.3f" % M76_value_call_MCS(S0))
Value of Call Option 20.013
print("Value of Call Option %8.3f"
% M76_value_call_FFT(S0, K, T, r, sigma, lamb, mu, delta))
Value of Call Option 19.948
接下来对不同行权价的数据进行模拟。
S0 = 100 # initial index level
K = np.linspace(70,150,20) # strike level
T = 1.0 # call option maturity
r = 0.05 # constant short rate
sigma, lamb, mu, delta = [0.4, 1.0, -0.2, 0.1]
Merton_lewis=[]
for i in range(len(K)):
Merton_lewis.append(M76_value_call_INT(S0, K[i], T, r, sigma, lamb, mu, delta))
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
import matplotlib.pyplot as plt
plt.figure(figsize=(12,10))
plt.plot(K,Merton_lewis_new,'r-',label='lewis')
plt.plot(K,Merton_mcs_new,'g^',label='MCS')
plt.plot(K,Merton_fft_new,'b--',label='FFT')
plt.xlabel('strike')
plt.ylabel('value')
plt.legend()
plt.show()
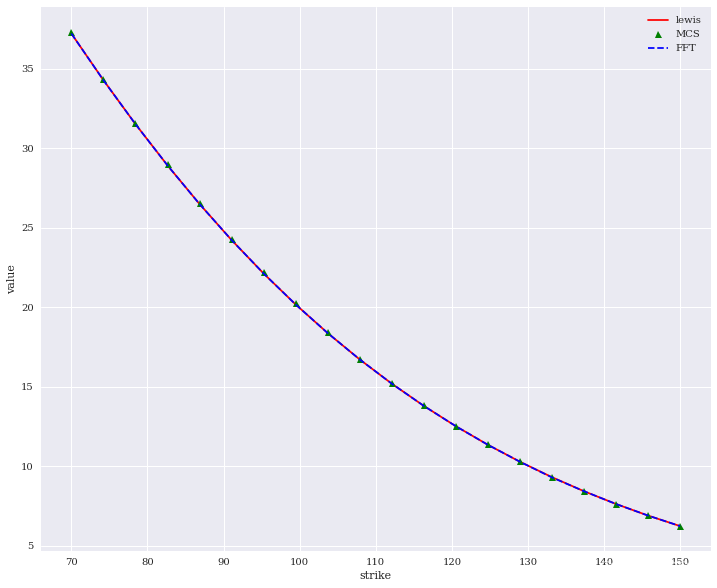
通过上图可以看出,三种方法所得的结果大致是相等的。
五、Merton模型的校准
校准部分采用上证50ETF期权数据
import math
import numpy as np
import pandas as pd
import scipy.optimize as sop
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'serif'
np.set_printoptions(suppress=True,
formatter={'all': lambda x: '%5.3f' % x})
数据如下所示:

部分代码:
# Option Selection
tol =0.9
S0 =4.736 #
r =0.015 #
options = data[(np.abs(data['行权价'] - S0) / S0) < tol].copy()
options['交易时间'] = pd.DatetimeIndex(options['交易时间'])
options['到期日'] = pd.DatetimeIndex(options['到期日'])
#
# Error Function
#
def M76_error_function_FFT(p0):
''' Error Function for parameter calibration in M76 Model via
Carr-Madan (1999) FFT approach.
Parameters
==========
sigma: float
volatility factor in diffusion term
lamb: float
jump intensity
mu: float
expected jump size
delta: float
standard deviation of jump
Returns
=======
RMSE: float
root mean squared error
'''
global i, min_RMSE
sigma, lamb, mu, delta = p0
if sigma < 0.0 or delta < 0.0 or lamb < 0.0:
return 500.0
se = []
for row, option in options.iterrows():
T =option['剩余到期日']
model_value = M76_value_call_INT(S0, option['行权价'], T, r, sigma, lamb, mu, delta)
# M76_value_call_FFT(S0, option['行权价'], T,r, sigma, lamb, mu, delta)
se.append((model_value - option['收盘价']) ** 2+0.001)
RMSE = math.sqrt(sum(se) / len(se)) #RMSE(Root Mean Square Error)均方根误差
min_RMSE = min(min_RMSE, RMSE)
if i % 50 == 0:
print('%4d |' % i, np.array(p0), '| %7.3f | %7.3f' % (RMSE, min_RMSE))
i += 1
return RMSE
校准结果如下
0 | [0.075 0.100 -0.500 0.100] | 0.106 | 0.106
50 | [0.075 0.300 -0.100 0.300] | 0.084 | 0.082
100 | [0.100 0.200 -0.200 0.200] | 0.098 | 0.060
150 | [0.125 0.100 -0.300 0.100] | 0.092 | 0.057
200 | [0.125 0.400 -0.500 0.300] | 0.064 | 0.057
250 | [0.150 0.200 0.000 0.200] | 0.073 | 0.052
300 | [0.175 0.100 -0.100 0.100] | 0.070 | 0.047
350 | [0.175 0.400 -0.300 0.300] | 0.049 | 0.044
400 | [0.200 0.300 -0.400 0.200] | 0.044 | 0.043
450 | [0.197 0.392 -0.099 0.326] | 0.042 | 0.042
500 | [0.138 0.290 -0.101 0.546] | 0.042 | 0.042
550 | [0.140 0.288 -0.100 0.540] | 0.042 | 0.042
600 | [0.104 0.410 -0.328 0.632] | 0.042 | 0.042
650 | [0.107 0.409 -0.322 0.623] | 0.042 | 0.042
700 | [0.100 0.412 -0.349 0.642] | 0.042 | 0.042
750 | [0.100 0.412 -0.348 0.642] | 0.042 | 0.042
800 | [0.100 0.413 -0.348 0.641] | 0.042 | 0.042
850 | [0.101 0.429 -0.324 0.616] | 0.042 | 0.042
900 | [0.101 0.435 -0.317 0.608] | 0.042 | 0.042
950 | [0.099 0.489 -0.276 0.554] | 0.042 | 0.042
1000 | [0.099 0.549 -0.241 0.504] | 0.042 | 0.042
1050 | [0.097 0.596 -0.221 0.475] | 0.042 | 0.042
1100 | [0.098 0.632 -0.204 0.450] | 0.042 | 0.042
1150 | [0.096 0.714 -0.179 0.411] | 0.042 | 0.042
可以看出,最优的参数校准结果为:0.096 0.714 -0.179 0.411
六、Merton模型的实证分析
使用上证50ETF期权数据进行实证分析,参数使用校准后的数值。
#
S0 =data['标的资产价格'] # initial index level
K = 5.25 # strike level
T = data['剩余到期日'] # call option maturity
r = data['无风险利率']/100 # constant short rate
sigma = 0.096 # constant volatility of diffusion
lamb = 0.714 # jump frequency p.a.
mu = -0.179 # expected jump size
delta = 0.411 # jump size volatility
t=0
数值积分方法定价结果如下所示
label=data['收盘价']
# mape
mape=np.mean(np.abs((pred-label)/label))
# rmse
rmse=np.sqrt(np.mean(np.square(pred-label)))
# mae
mae=np.mean(np.abs(pred-label))
#MSE
mse=np.sum((label-pred)**2)/len(pred)
print('Merton模型(数值积分)测试集的mape:',mape,' rmse:',rmse,' mae:',mae,'MSE:',mse)
Merton模型(数值积分)测试集的mape: 1.245930578947643 rmse: 0.05159869865802706 mae: 0.03353124034422371 MSE: 0.0026624257032018834
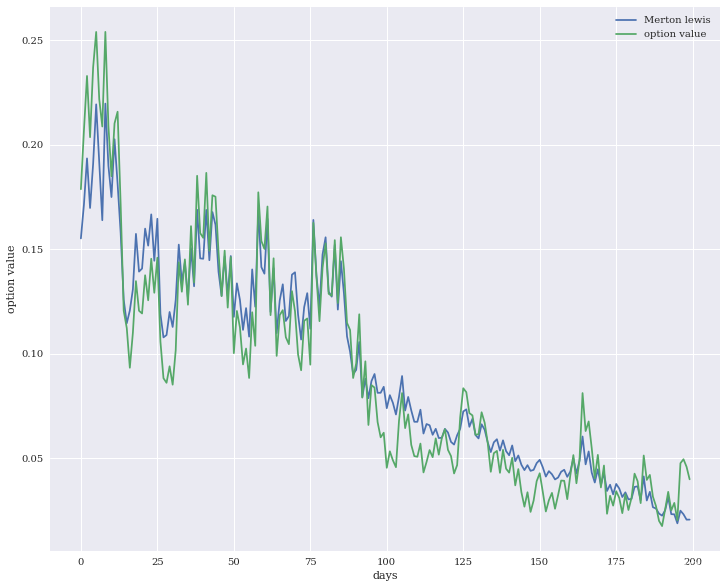
总结
本章对Merton模型进行了介绍,并且使用了三种方法进行定价,使用实际市场数据进行了Merton参数校准。最后基于校准的参数进行了上证50ETF期权的定价。