[人工智能] 《Curriculum-Meta Learning for Order-Robust Continual Relation Extraction》论文笔记

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 《Curriculum-Meta Learning for Order-Robust Continual Relation Extraction》论文笔记 -> 正文阅读

[人工智能]《Curriculum-Meta Learning for Order-Robust Continual Relation Extraction》论文笔记

Curriculum-Meta Learning for Order-Robust Continual Relation Extraction

这篇文章的阅读方式尝试用沐神建议的方法进行~

1. Abstract

连续关系提取是从非结构化文本中逐步提取新事实的一项重要任务。根据这些关系的顺序到达顺序，该任务容易面临两个严重的挑战，即灾难性遗忘和顺序敏感性。本文提出了一种新的curriculum-meta learning方法来解决连续关系提取中的上述两个挑战。作者将 meta learning and curriculum learning相结合，以快速适应新任务，并减少先前看到的任务对当前任务的干扰。通过关系域和范围类型的分布，设计了一种新的关系表示学习方法。这种表示被用来量化构建课程的任务的难度。此外，作者还提出了新的基于难度的度量标准来定量衡量给定模型的顺序敏感性程度，为评估模型的鲁棒性提供了新的方法。本文在三个基准数据集上的综合实验表明，所提出的方法优于最先进的技术。

2. Introduction

2.1 理论知识

关系提取RE目的是从非结构化文本中提取结构化事实。然而，由于存储和计算资源的限制，授予关系提取器对以前看到的任务中的所有训练实例的访问权限是不切实际的。而持续学习公式与传统的关系提取设置相反，它的提取器通常是从头开始进行训练的，并且可以完全访问训练语料库。

**Catastrophic Forgetting (CF) **灾难性遗忘指的是当一个神经网络被用来学习一系列任务时，对后期任务的学习可能会降低学习模型对之前任务的性能。现有对灾难性遗忘方法的探究也从CV领域扩展到了NLP领域，但这些方法大多探讨了任务序列整体性能中的CF问题，从而缺乏对每个子任务的特征和相应的模型性能的洞察力分析。

**Order-sensitivity (OS)**顺序敏感性是持续学习中的另一个主要问题，它是指任务的性能随任务到达序列的顺序不同而变化的现象。这不仅是由于之前任务的不同序列所产生的CF，而且也是由于来自前一个任务的单向知识转移。OS可能在各个方面都存在问题：

持续学习中的伦理人工智能考虑，例如医学领域的公平性；
连续学习算法的基准标记，因为大多数现有的工作选择一个任意和随机的给定任务序列进行评估；
在知识库群体的现实场景中，提取知识的质量存在不确定性。

2.2 文章内容

本文介绍了curriculum-meta learning(CML)方法，以解决灾难性遗忘和顺序敏感性问题。CML采用基于记忆的方法，基于以下对以往研究中灾难性遗忘和顺序敏感性问题的观察：

与经验记忆的过拟合，表明任何任务的表现都会随着训练的进展而下降
相似任务之间的干扰，表明该模型在侵入性较小的任务上表现更好。

作者设计了一种机制，选择性地降低记忆的回放频率，以避免过拟合，并引导模型学习当前任务和之前最相似任务之间的偏差，以降低顺序敏感性。

CML方法包含两个步骤：

在第一步中，它根据当前任务的先前任务的差异性从内存中采样实例，从而生成一个持续学习的课程。
然后，对当前任务的课程和训练实例进行训练。

作者进一步介绍了一种基于知识的方法，根据关系对的相似性来量化任务难度。摘要将关系作为映射到其域和范围内命名实体的函数，根据头尾实体的概念分布定义了两个关系之间的相似性度量。

2.3 Contribution

提出了一种新的curriculum-meta learning来解决连续关系提取中的顺序敏感性和灾难性遗忘问题。
通过关系头尾实体的概念分布，引入了一种新的关系表示学习方法，用来量化每个关系提取任务的差异。
我们进行了全面的实验来分析最先进的方法中的顺序敏感性和灾难性遗忘问题，并通过经验证明了我们提出的方法在三个基准数据集上优于最先进的方法。

3. Conclusion

本文提出了一种新的curriculum-meta learning方法，以解决持续关系学习中的灾难性遗忘和顺序敏感性问题。课程的构建是基于任务难度的概念，这是通过一种新的关系表示学习方法，从关系的分布中学习。本文在三个基准数据集上对连续简单问题和连续跟踪的综合实验表明，所提出的方法优于最先进的模型，不容易发生灾难性遗忘和顺序敏感。未来，作者将基于本文提出的框架，研究一种终端终端课程模型和一种新的动态难度测量方法。

4. Related work

传统的关系提取方法可以根据数据的使用方式分为三个领域：监督、半监督和远程监督。这些方法大多都假设了一个预先定义的关系模式，因此不容易被推广到新的关系中。为了克服这一问题，人们提出了一些具有挑战性的任务，包括开放关系学习和连续关系学习，以在没有预定义关系模式的情况下检测和学习关系。

灾难性遗忘(CF)是持续学习的重要研究方向，处理CF的方法可以大致分为三类：

基于整合的方法：巩固对之前任务重要的模型参数，并减少它们的学习权重。主要使用复杂的机制来评估参数对任务的重要性。
动态架构方法：动态扩展模型架构以学习新任务，有效防止旧遗忘任务。这些方法的大小随着新任务的增加而急剧增长，这使得它们不适合用于NLP应用程序。
基于记忆的方法：记住旧任务中的一些例子，不断地通过新任务来学习它们，以减轻灾难性的遗忘。

在这些方法中，基于内存的方法已被证明是最有前途的NLP应用。

5. Method

5.1 Problem Formulation

在连续关系提取中，给定 $K$ 个任务序列 ${T_1,T_2,...,T_k\}$ 每个任务 $T_k$ 是传统的监督分类任务，包含一系列例子及其对应的标签 ${(x^{(i)},y^{(i)}\}$ ，其中 $x^{(i)}$ 是输入数据，包含自然语言上下文和候选关系， $y^{(i)}$ 是上下文的基本真关系标签。模型 $f_θ(.)$ 可以访问当前任务 $D_k^{train}$ 的训练数据，并通过优化损失函数 $l(f_θ(x),y)$ 进行训练。持续学习的目标是训练模型 $f_θ(.)$ ，这样它就会不断地学习新的任务，同时避免灾难性地忘记以前学到的任务。由于各种限制，学习者通常只允许维护和观察之前任务的训练数据的子集，该数据包含在内存集 $M$ 中。

模型 $f_θ(.)$ 的性能采用常规方法进行测量，通过全精度 $Acc_w=acc_{f,D^{test}_i}$ ，在整个测试集上进行测试，其中 $D_{test}=\bigcup^K_{i=1}D_i^{test}$ 。此外，在序列 $Acc_a=\frac{1}{k}\sum_{i=1}^kacc_{f,i}$ 中，以所有任务的测试集的平均精度来评估任务k下的模型性能。平均准确性是衡量灾难性遗忘影响的更好方法，因为它强调了模型对早期任务的表现。

5.2 Framework

在这里插入图片描述

CML维护初始化参数 $θ_t$ 和存储以前任务的原型实例的内存集 $M$ 。它在学习阶段的每个时间步长 $t$ 上执行以下操作。

元学习者 $L$ 从存储器中获取初始化参数 $θ_t$ 来初始化模型 $f_{θ_t}(.)$ 。
$L$ 在课程集 $D_{t,i}^{curri}$ 上回放，它由基于知识的课程模块进行抽样和排序。
$L$ 在支持集 $D_{t,i}^{train}$ 上训练当前任务 $T_t$ 。
最后，L更新学习到的参数 $θ_{t+1}$ ，并将当前任务的少量原型实例存储到内存中。

在评估阶段，训练后的模型被赋予一个目标集，其中包含所有观察任务的看不见实例(CML的工作流程见附录a)。

文章将从（1）对初始化参数的利用（即元训练）和（2）对内存集的利用（即基于课程的记忆重放）的角度来介绍该框架。

5.2.1 Meta Training

元学习旨在开发算法来学习如何从给定的任务分布中解决任务的通用知识。利用一个给定的基本关系提取模型 $f_θ(.)$ 通过 $θ$ 参数化，采用基于梯度的元学习方法在每个时间步 $t$ 学习预先初始化 $θ_t$ 。在适应新任务时，模型参数 $θ$ 从 $θ_t$ 快速更新到特定任务的 $θ_t^?$ ，需要几步梯度下降。形式上，元学习者 $L$ 更新 $f_θ(.)$ 也就是针对以下目标进行了优化：

$min_\theta E_{\tau \sim p(T)}[L(\theta^*)]=min_\theta E_{\tau \sim p(T)}[L(U(D_\tau \theta))]$

其中 $D_\tau$ 为训练数据， $L$ 为任务 $T$ 的损失函数， $\bigcup$ 为 $f_θ(.)$ 的优化器。然后，当它收敛于当前任务时，模型将为下一个时间步t+1生成初始化参数 $θ_{t+1}$ ：

$\theta_{t+1}=\theta+\frac{\epsilon}{n}\sum_{t=1}^n(\theta^*_t-\theta_t)$

其中， $θ_t^?$ 是在时间步 $t$ 时当前任务 $T_k$ 的更新参数， $n$ 是在时间步中可以并行处理的实例数。

5.2.2 Curriculum-based Memory Replay

元学习者 $L$ 在学习新任务之前，会有序地回顾之前的任务。本文用 $g_\phi(.)$ 来表示一个为学生网络准备课程的教师函数，即关系提取器 $f_θ(.)$ ，以进行replay。与传统的基于经验回放的模式不同，教师的功能需要掌握三种技能：

评估任务的难度。当新任务到达时，此函数计算所有观察到的先前任务中哪一个干扰当前任务。
从内存中采样实例。通过采样，可以减少重放阶段的时间消耗，缓解内存上高频率更新导致的过拟合问题。
根据特定的策略对抽样的实例进行排序。教师指导学生模型以最有效的方式学习当前任务和观察相似任务之间的偏差。

作者对内存进行随机抽样，并根据之前每个任务相对于当前任务的难度对抽样实例进行排序。基于上述要求，实现了一个基于知识的课程模块，也就是Knowledge-based Curriculum。

5.3 Knowledge-based Curriculum

本质上，顺序敏感性是由于模型无法保证之前所有任务的最佳性能而造成的。然而，从实验的角度来看，顺序敏感性与不同任务的不平衡遗忘率（或不平衡难度）密切相关，我们假设任务难度是由于观察到的任务序列中语义相似关系之间的相互作用。直观地说，如果两种关系的概念分布相似，那么这两种关系往往会在相似的自然语言语境中表达出来，如关系“父亲”和“母亲”。

5.3.1 Semantic Embedding-based Difficulty Function

为了使这种直觉形式化，定义了一个基于每个任务中关系的语义嵌入的难度估计函数。给定一组 $K$ 个任务 ${T_1,T_2,...,T_K\}$ ，任务 $T_i$ 的差异定义为：

$Dl_i:=\frac{1}{K-1}\sum_{j=1,j\neq i}^K S_i^j$

$S^j_i$ 是任务 $T_i$ 和 $T_j$ 之间的相似度得分，定义为两个任务的关系对之间的平均相似度：

$S_i^j:=\frac{1}{M\times N}\sum_{m=1}^M\sum_{m=1}^Ms_m^n$

其中，M和N分别是每个任务中的关系数， $s^n_m$ 计算这两个关系的嵌入之间的余弦相似性： $s^n_m:=cos(emd_m，emd_n)$ 。利用 $s^n_m$ 计算记忆中每个关系与当前任务中关系的难度，以便对存储在记忆中的关系进行排序和抽样到最终课程中。

5.3.2 Relation Representation Learning

为了计算每个关系的语义嵌入，本文介绍了一种基于知识和分布的表示学习方法。直观地说，一个关系的表示是从其头部和尾部实体的类型中学习出来的。考虑一个知识图 $G=\{(h,r,t)∈E×R×E\}$ ，其中 $h 和 t$ 是头实体和尾实体， $r$ 是它们之间的关系，E和R分别表示实体集和关系集。将关系表示学习任务简化为学习每个关系的概念分布的问题，该问题根据以下目标进行优化：

$min_\phi L(\phi;G)=min_\phi \sum_{(h',t';r)∈G}[-\log P_\phi(h'|r)-\log P_\phi(t'|r)]$

其中， $h^{'}$ 和 $t^{'}$ 分别为头实体和尾实体的概念。 $P_\phi(h'|r)=\exp(NN_{\phi_1}(h',r))$ 和 $P_\phi(t'|r)=\exp(NN_{\phi_2}(t',r))$ ，其中 $NN_{\phi}(a,b)=MLP_\phi (a)^{\top}b$ 是由 $\phi$ 参数化的两层神经网络。最后，得到了每个关系的两种表示形式 $emd^h_r$ 和 $emd^t_r$ ，它们分别表示了头部实体和尾部实体的概念分布。最后将这两个嵌入连接起来，以生成关系 $emd^r:=[emd^h_r;emd^t_r]$ 的最终表示。

6. Experiment

6.1 Main Results

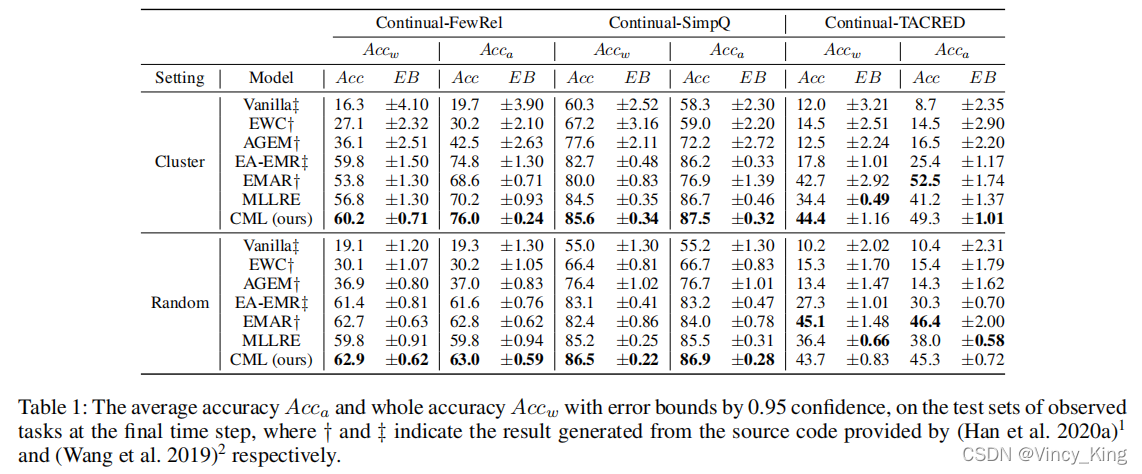
在这里插入图片描述

CML在两种情况下和在大多数情况下在三个数据集和两个较大的数据集 Continual-FewRel and Continual-SimpQ上都达到了最好的 $Acc_w和Acc_a$ 。
CML在大多数情况下获得了最低的误差界EB，表现出更好的稳定性和较低的阶灵敏度。
这两种任务划分方法在CML中产生了最显著的 $Arcc_a$ 差异。当数据均匀分布（即随机）时，CML的 $Acc_a显著降低到几乎等于Acc_w$ （从76.0到63.0）。在其他两个数据集上，性能差异远不那么明显。

6.2 Analysis of Unbalanced Forgetting

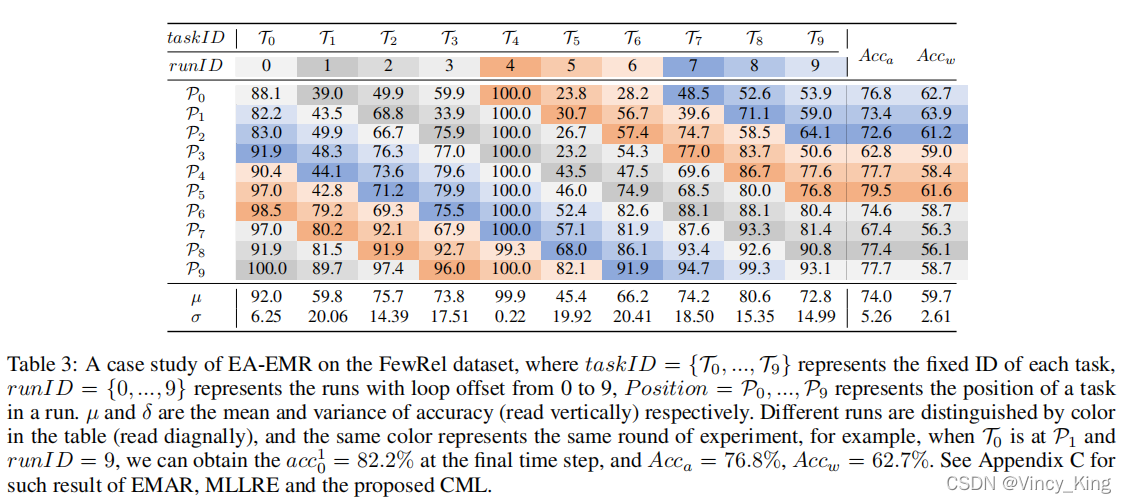
在这里插入图片描述

比较结果行 $P_0和P_9$ 的每个任务，我们可以观察到，大多数任务看到精度显著下降从 $P_9$ （当任务是最后一个模型） $P_0$ （当任务是第一个模型），表明他们遭受灾难性的遗忘。
表3中的每一列中每个任务的遗忘率是不同的，这不能仅仅用记忆过拟合的问题来解释。例如， $P_9$ 模型在 $T_4和T_0$ 上的性能正好是100。但是，在 $T_4$ 上的性能并不会随着其位置的提高而下降。另一方面，可以观察到随着 $T_0$ 的位置后退，它的性能呈下降趋势。
顺序敏感性可能与运行中早期任务的难度有关，其中差异性指的是一个任务更容易被模型遗忘的趋势。例如，runID=4实验的最终 $Acc_a$ （暗橙色）是最高的，而runID=6实验的最终 $Acc_a$ （浅橙色）是最低的。此外，在 $P_0位置的所有任务中，任务T_4的准确率最高，而任务T_6$ 的准确率最低。
作者假设这很可能是由于有限的任务相关记忆的频繁回放，换句话说，是对记忆的过拟合，所以接下来通过调整训练数据与记忆的比例来验证这个假设。

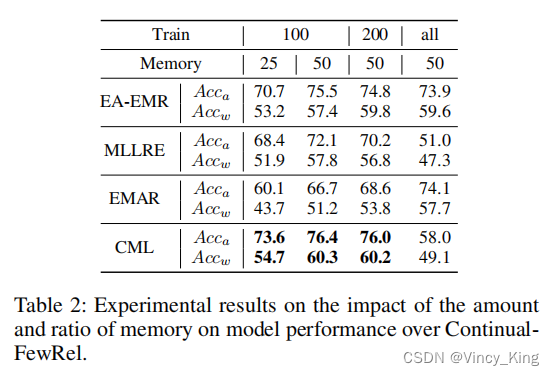
在这里插入图片描述

当内存大小固定时，更多的训练数据导致除EMAR外的所有模型的性能较差，表明该模型对内存过拟合。这是由于内存的重播频率更高。当确定训练数据与内存的比值（例如100：25和200：50）时，模型的性能符合使用更多数据时具有更好的性能的一般规则。

6.3 Analysis of Task Difficulty

6.3.1 Qualitative Analysis
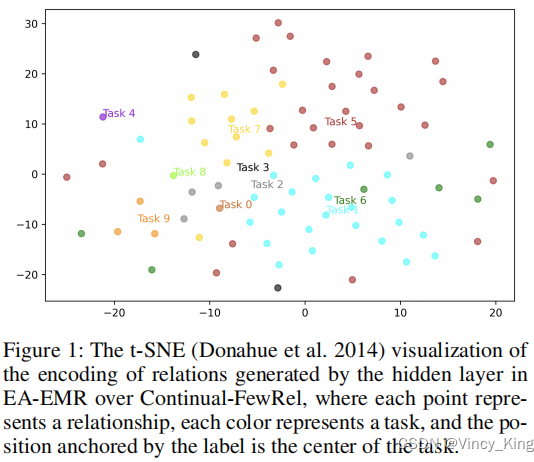
在这里插入图片描述

任务T4和T8各只有一个关系，并且T4中的关系与其他关系很远，但关系T8更近。他们与其他关系的距离差异可能解释了表3中他们的特定任务表现的差异，其中T4没有遭受灾难性遗忘，但T8有。换句话说，T4很容易，而T8更难。
T3（黑色）只包含两个关系，它与其他任务显著重叠。因此，T3上的灾难性遗忘更为严重，即T3上的困难。
因此，在持续学习中，任务T的难度可能表现为T与其他观察到的任务之间的相关性。在关系提取场景中，将这种关联定义为关系之间的语义相似性。

6.3.2 Quantitative Analysis

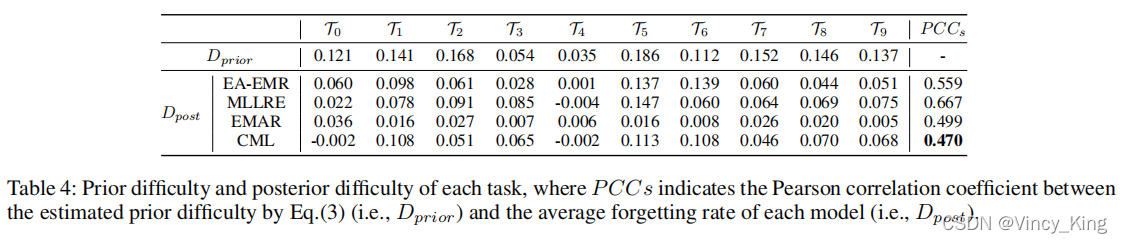
三种模型的PCCs（表示由等式估计的先验难度之间的皮尔逊相关系数(即 $D_{prior})$ 和每个模型的平均遗忘率(即 $D_{post})$ ）表明，基于语义嵌入的先验难度对遗忘率有利，说明哪些任务是困难的。
将CML与其他三种方法的PCCs值进行比较，本文提出的CML确实降低了相似任务的遗忘率，从而减轻了相似任务之间的干扰。
对于CML中的任务 $T_0和T_4$ ，平均遗忘率为负，这意味着这些任务的准确性随着它们接近尾声而降低。
从表1、表3的分析可以明显看出，CML提高了整体精度，有效缓解了顺序敏感性问题。但这些改进的代价是对T0和T4等简单任务的准确性的适度降低。