MonoPair: Monocular 3D Object Detection Using Pairwise Spatial Relationships

概要

单目三维目标检测的好处有低成本、低耗能、应用灵活等，但它的局限性之一就是对部分可见的样本难以检测，这是因为大多数检测器把每个三维物体当成独立的训练目标，那么部分被遮挡的物体就难以被get到。
如果直接来解决这个问题，大多使用网络来获得更多的信息，但是这种进步空间不大。
基于此，文章考虑了配对样本关系来提出新方法。利用离得近的物体的空间关系而不是独立地关注在这一个被遮挡的物体上。对部分遮挡的物体根据它们的邻近区域对空间约束进行编码，具体来说，检测器会对邻近物体对的物体位置与三维距离以无监督学习方式计算不确定性感知预测，然后通过图优化框架用非线性最小二乘进行联合优化。不确定性用来决定损失函数每一项的权重*(使用不确定性来加权后优化的代价函数)*。最后，将单阶段不确定性感知预测结构和后优化模块进行整合以保证运行效率。
方法在KITTI 3D检测基准上获得了最好的性能。
方法总体结构：
在这里插入图片描述
该结构包括一个backbone网络（使用的是DLA-34)和几个具体任务密集预测分支。backbone网络以单目图像为输入，以(W×H×64)大小的特征图为输出,是通过有监督方式训练，虚线表示神经网络向前流动。然后经过三个橙色模块后有11个输出分支，每个分支大小为(W×H×m),这11个输出分支被分成了三个部分（如图）

方法细节

注： $c^g$ ：关键点位置； $w^b,h^b)$ :bounding box大小； $c^b$ :bounding box中心； $c^w$ :世界坐标系下物体中心， $c^o$ :在特征图中的投影

2D检测
这个模块是从CenterNet中获取，输出的heatmap是用于确定关键点位置和分类，另外两个分支输出bounding box的大小和偏移量 $(\delta^v,\delta^u)$ ，这些量以特征图坐标为单位。
3D检测
相机内置矩阵和导出 $c^w$ 的表达式：
在这里插入图片描述
深度分支预测出来的是 $\hat{z}$ , $z=1/\sigma(\hat{z})-1$ dimension分支直接回归出(w,h,l),2D检测和3D检测中的深度、偏移量和大小分支都是使用L1 loss来训练的。
另外朝向的话，我估计的是局部朝向 $\alpha$ ,它是对于物体相对于相机的视角 $\gamma$ 的。朝向用8个标量表示，这个分支用MultiBin损失训练。
配对空间约束
这块定义一个回归目标来估计位置临近的物体的配对几何约束，配对策略：任意俩2D bounding box的中心为直径画个圆，圆内要是包含另一个bbox的中心点，这一对就不用考虑了。（如下）
在这里插入图片描述
配完对的效果：

对于配好的一对，特征图上的配对约束关键点是 $c_i^b+c_j^b)/2$ ,回归目标是配对约束分支输出的三维距离。

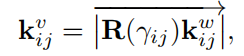
其中 $k_{ij}^w=c_i^w-c_j^w$ （相机坐标系下）
$\gamma_{ij}=arctan(p_x^w/p_z^w)$

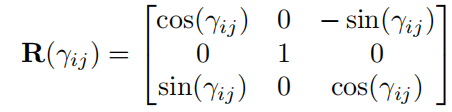
由于相机坐标系下的不同角度下的距离不变性，三维空间下的绝对距离我们不用 $k^w$ 而用 $k^v$ 。
Uncertainty
用L1损失定义回归任务：
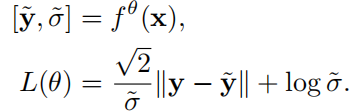
在这里插入图片描述
x:输入数据
y:groungtruth 回归目标
$\hat{y}$ :预测的结果
$\hat{\sigma}$ :模型的另一个输出，可以代表x的观测噪声（偶然不确定性，在本文章中出现在三个分支里面，主要用于确定error的权重）
$\theta$ :回归模型的权重
空间约束优化
用了一个图模型，顶点是配对了的目标，边是配对了的约束。
优化形式：（非线性最小化二乘问题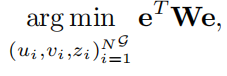）在这里插入图片描述
e:error向量
W:不同error的权重矩阵
例子：

配对约束error
对每一对，有三个错误项 $e_{ij}^x,e_{ij}^y,e_{ij}^z)$ 衡量网络估计的三维距离和 $k_{ij}^v$ 的差距，如下：
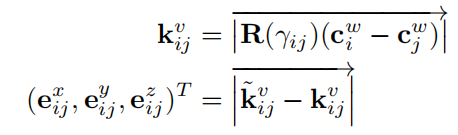
目标位置error
衡量网络估计出来的目标位置和优化的位置的偏差：
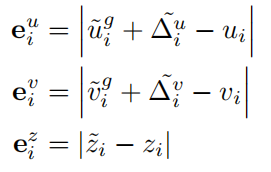
权重矩阵
不确定性越低，对应的error权重会更高（why higher),所以W的一个因子是 $1/\hat{\sigma}$ ,有了置信区间，配对约束和目标位置error可以一起被最小化。