Overview
这三个东西的话,都是用来算相似度的,用更准确的说法应该叫 ∣ ∣ L ∣ ∣ 1 ||L||_1 ∣∣L∣∣1?, ∣ ∣ L ∣ ∣ 2 ||L||_2 ∣∣L∣∣2?, ∣ ∣ L ∣ ∣ ∞ ||L||_{\infty} ∣∣L∣∣∞?,即数值分析中的1-范数、2-范数、无穷范数。接下来为了方便描述起见仅以二维空间下的两点 A ( x 1 , y 1 ) A(x_1,y_1) A(x1?,y1?), B ( x 2 , y 2 ) B(x_2,y_2) B(x2?,y2?)为例。
L1距离
即曼哈顿距离,可以简单理解为只能横着走或竖着走: d 1 = ∣ x 1 ? x 2 ∣ + ∣ y 1 ? y 2 ∣ d_1=|x_1-x_2|+|y_1-y_2| d1?=∣x1??x2?∣+∣y1??y2?∣
L2距离
即欧氏距离,也是我们平时最常用的,两点之间的直线距离: d 2 = ( x 1 ? x 2 ) 2 + ( y 1 ? y 2 ) 2 {d_2} = \sqrt {{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2}} d2?=(x1??x2?)2+(y1??y2?)2?
L-Inf距离
即切比雪夫距离,可以理解为国际象棋中国王的走子法,有八个方向可以移动: d ∞ = max ? ( ∣ x 1 ? x 2 ∣ , ∣ y 1 ? y 2 ∣ ) {d_\infty } = \max (|{x_1} - {x_2}|,|{y_1} - {y_2}|) d∞?=max(∣x1??x2?∣,∣y1??y2?∣)
Summary
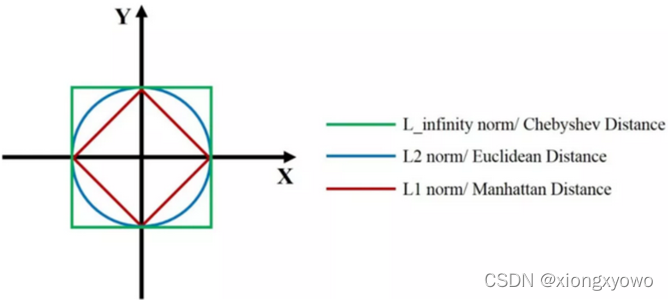
考虑这三种距离,距原点
(
0
,
0
)
(0,0)
(0,0)为1的所有点构成的集合如下: