参考书目:数学教科书,作者:我妻幸长
文章目录
什么是概率
P
(
A
)
=
a
n
P(A)=\frac{a}{n}
P(A)=na?
其中P(A)是事件A发生的概率,a是A事件发生场景的数量,n是所有场景发生的数量
例如抛硬币,有正面和反面两种情况则n=2,若A代表正面的情况,a=1,即
P
(
A
)
=
1
2
P(A)=\frac{1}{2}
P(A)=21?
补事件
P
(
A
ˉ
)
=
1
?
P
(
A
)
P(\bar{A})=1-P(A)
P(Aˉ)=1?P(A)
例如掷骰子,两个骰子点数之和为5的事件是A,则
P
(
A
)
=
1
9
P(A)=\frac{1}{9}
P(A)=91?,则补事件:点数之和不为5的概率为
P
(
A
ˉ
)
=
1
?
1
9
=
8
9
P(\bar{A})=1-\frac{1}{9}=\frac{8}{9}
P(Aˉ)=1?91?=98?
依概率收敛
当试验次数增多,$\frac{事件发生数}{试验数}$会向概率收敛#试验:掷一个骰子点数为5的概率收敛与1/6
import numpy as np
import matplotlib.pyplot as plt
x=[] #记录试验次数
y=[] #记录当前出现5的概率
total=0#总试验次数
num_5=0#骰子出现5的次数
n=5000#掷骰子次数
for i in range(n):
if np.random.randint(6)+1 == 5:
num_5+=1 #因为python中数字类型不可改变所以没有++(--)运算符,每次值发生改变都是申请一块内存赋新值
total += 1
x.append(i)
y.append(num_5/total)
plt.plot(x,y)
plt.plot(x,[1/6]*n,linestyle="dashed")#注:将列表1/6重复n次
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
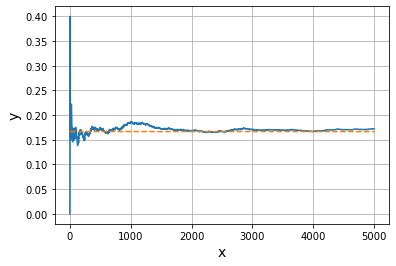
可以看出随着试验次数增加
5
出
现
次
数
试
验
数
\cfrac{5出现次数}{试验数}
试验数5出现次数? 向概率16.7%收敛
平均值和期望值
平均值:
μ
=
∑
k
=
1
n
x
k
\mu=\sum\limits_{k=1}^n x_k
μ=k=1∑n?xk?
#numpy.averge()函数计算平均值
x=np.array([42,53,56,32,75])
print(np.average(x))
51.6
期望值:
E
=
∑
k
=
1
n
P
k
x
k
E=\sum\limits_{k=1}^n P_kx_k
E=k=1∑n?Pk?xk?
其中
P
k
P_k
Pk?是获得值
x
k
x_k
xk?的概率
#示例:
p=np.array([0.8,0.15,0.05])#概率
x=np.array([100,500,1000])#值
print(np.sum(p*x))
205.0
平均值与期望关系的推导
将平均值写为
1
n
∑
k
=
1
n
n
k
x
k
\frac{1}{n}\sum\limits_{k=1}^n n_kx_k
n1?k=1∑n?nk?xk?,其中
n
k
n_k
nk?为值
x
k
x_k
xk?出现的次数
而
n
k
n_k
nk?满足
∑
k
=
1
n
n
k
=
n
\sum\limits_{k=1}^n n_k=n
k=1∑n?nk?=n
变形为
∑
k
=
1
n
n
k
n
x
k
\sum\limits_{k=1}^n \frac{n_k}{n}x_k
k=1∑n?nnk??xk?
将
n
k
n
\frac{n_k}{n}
nnk??看做概率
P
k
P_k
Pk?
则平均值表达式可写为
∑
k
=
1
n
P
k
x
k
\sum\limits_{k=1}^nP_kx_k
k=1∑n?Pk?xk?与期望值表达式相同,意味着是同一个概念。
方差与标准差
方差表达式:
V
=
1
n
∑
k
=
1
n
?
x
k
?
μ
?
2
V=\frac{1}{n}\sum\limits_{k=1}^n \lgroup x_k-\mu \rgroup^2
V=n1?k=1∑n??xk??μ?2
其中
μ
\mu
μ是平均值
标准差为方差的平方根
σ
=
V
\sigma=\sqrt{V}
σ=V?
#numpy实现方差numpy.var()
import numpy as np
x_1=np.array([55,49,60,40])
x_2=np.array([51,49,52,48])
print(np.var(x_1))#x_1的方差
print(np.var(x_2))#x_2的方差
#numpy.std()实现标准差
print(np.std(x_1))
print(np.std(x_2))
55.5
2.5
7.44983221287567
1.5811388300841898
正态分布
正态分布又称高斯分布,非常适用于自然界和人类行动、特性等各种现象的数据分布
f
(
x
)
=
1
σ
2
π
exp
?
(
?
(
x
?
μ
)
2
2
σ
2
)
f(x)=\frac{1}{\sigma \sqrt{2\pi}} \exp\big(-\frac{(x-\mu)^2}{2\sigma^2}\big)
f(x)=σ2π?1?exp(?2σ2(x?μ)2?)
若平均值
μ
=
0
\mu=0
μ=0和标准差
σ
=
1
\sigma=1
σ=1时可化简为
f
(
x
)
=
1
2
π
exp
?
(
?
x
2
2
)
f(x)=\frac{1}{\sqrt{2\pi}}\exp\big(-\frac{x^2}{2}\big)
f(x)=2π?1?exp(?2x2?)
#绘制正态分布曲线
import numpy as np
import matplotlib.pyplot as plt
def pdf(x,mu,sigma):#mu:平均值,sigma:标准差
return 1/(sigma*np.sqrt(2*np.pi))*np.exp(-(x-mu)**2/(2*sigma**2))
x=np.linspace(-5,5)
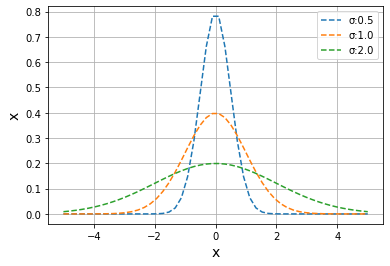
y_1=pdf(x,0.0,0.5)#平均值0,标准差0.5,不难发现平均值就是最大值所在的位置
y_2=pdf(x,0.0,1.0)#平均值0,标准差0.5
y_3=pdf(x,0.0,2.0)#平均值0,标准差0.5
plt.plot(x,y_1,label="σ:0.5",linestyle="dashed")
plt.plot(x,y_2,label="σ:1.0",linestyle="dashed")
plt.plot(x,y_3,label="σ:2.0",linestyle="dashed")
plt.legend()
plt.xlabel("x",size=14)
plt.ylabel("x",size=14)
plt.grid()
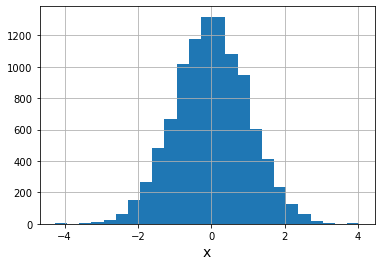
利用正太分布随机数画直方图
人工智能的参数常根据正态分布随机确定
#numpy.random.normal()
s=np.random.normal(0,1,10000)#表示平均值为0,标准差为1,产生10000个随机数
plt.hist(s,bins=25)
plt.xlabel("x",size=14)
plt.grid()
plt.show()
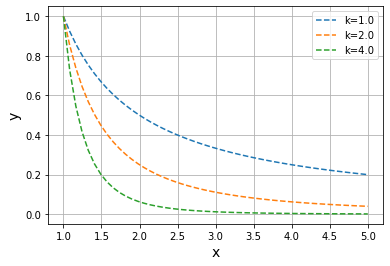
幂律
与正太分布一样,常用于自然和社会等各种现象,延伸范围比正太分布更广泛
f
(
x
)
=
c
x
?
k
f(x)=cx^{-k}
f(x)=cx?k
k=1时等式成反比,幂律的特征如同反比一样,延伸范围非常广泛
#绘制幂律图像
def power_func(x,c,k):
return c*x**(-k)
x=np.linspace(1,5)
y_1=power_func(x,1.0,1.0)
y_2=power_func(x,1.0,2.0)
y_3=power_func(x,1.0,4.0)
plt.plot(x,y_1,label="k=1.0",linestyle="dashed")
plt.plot(x,y_2,label="k=2.0",linestyle="dashed")
plt.plot(x,y_3,label="k=4.0",linestyle="dashed")
plt.legend()
plt.grid()
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.show()
遵循幂律的随机数
幂律分布中存在一种被称为帕累托分布的分布方法
f
(
x
)
=
a
m
a
x
a
+
1
f(x)=a\frac{m^a}{x^{a+1}}
f(x)=axa+1ma?
其中m与a为常数
画出其图像如下:
#numpy.pareto()生成帕累托分布的随机数
import numpy as np
import matplotlib.pyplot as plt
s=np.random.pareto(4,1000)#a=4,m=1,1000个
plt.hist(s,bins=25)
plt.xlabel("x",size=14)
plt.grid()
plt.show()
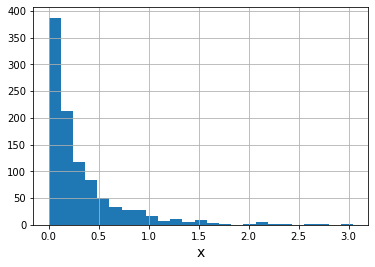
可以发现,x越大采样率越低。实际采用的数据经常遵循幂律,用人工智能处理问题要加以注意。
协方差
协方差表示两组数据之间关系的数值,常用于人工智能中的数据预处理。
X
=
x
1
,
x
2
,
?
?
,
x
n
Y
=
y
1
,
y
2
,
?
?
,
y
n
协
方
差
:
C
o
v
(
x
,
y
)
=
1
n
∑
k
=
1
n
(
x
k
?
u
x
)
(
y
k
?
u
y
)
X=x_1,x_2,\cdots,x_n \\ Y=y_1,y_2,\cdots,y_n \\ 协方差:Cov(x,y)=\frac{1}{n}\sum\limits_{k=1}^n(x_k-u_x)(y_k-u_y)
X=x1?,x2?,?,xn?Y=y1?,y2?,?,yn?协方差:Cov(x,y)=n1?k=1∑n?(xk??ux?)(yk??uy?)
协方差的含义:
- 协方差大(正):X较大时Y也较大,X较小时Y也有较小的倾向(正相关)
- 协方差接近0:X与Y的关系不大
- 协方差较小(负):X较大Y较小,X较小Y有较大倾向(负相关)
#示例
import numpy as np
import matplotlib.pyplot as plt
x=np.array([50,70,40,60,80])#数学得分
y=np.array([60,80,50,50,70])#英语得分
z=np.array([60,40,60,40,30])#语文得分
#计算x与y即数学得分和英语得分的协方差
cov_xy=np.average((x-np.average(x))*(y-np.average(y)))
print(cov_xy)
#数学与语文的协方差
cov_xz=np.average((x-np.average(x))*(z-np.average(z)))
print(cov_xz)
#画散点图表示他们间的关系
plt.scatter(x,y,marker="o",label="xy",s=40)#s为标记大小,marker是点的形状
plt.scatter(x,z,marker="x",label="xy",s=40)
plt.legend()
plt.grid()
plt.show()
120.0
-160.0
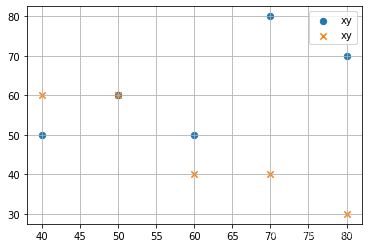
所以cov_xy是大于0的较大值,cov_xz是小于0的较小值
据协方差生成数据
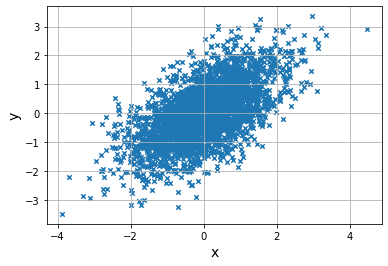
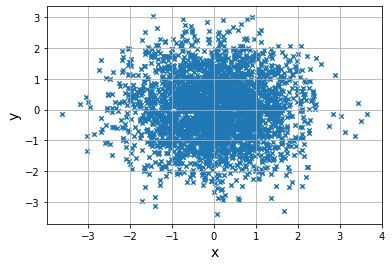
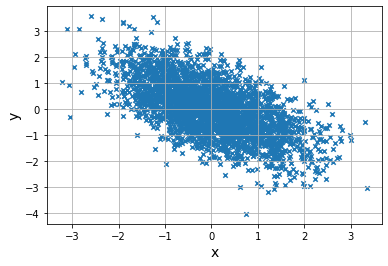
random.multivariaate_normal()函数使用协方差和正太分布生成数据,要求用矩阵指定协方差def show_cov(cov):#写一个协方差随机数图像函数
print("---Covariance:",cov,"---")
average=np.array([0,0])#分别为x和y的平均值
#协方差矩阵
cov_matrix=np.array([
[1,cov],
[cov,1]
])
#3000组数据3000个[x,y]
data=np.random.multivariate_normal(average,cov_matrix,3000)
#data呈现的矩阵形状是是(3000,2)
#取出横坐标
x=data[:,0]#第一列
y=data[:,1]#第二列
plt.scatter(x,y,marker="x",s=20)
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
#调用函数
show_cov(0.6)#正相关
show_cov(0)#不相关
show_cov(-0.6)#负相关
---Covariance: 0.6 ---
---Covariance: 0 ---
---Covariance: -0.6 ---
相关系数
ρ
=
C
o
v
(
x
,
y
)
σ
x
σ
y
\rho=\frac{Cov(x,y)}{\sigma_x\sigma_y}
ρ=σx?σy?Cov(x,y)?
?
1
≤
ρ
≤
1
?
ρ
-1\le\rho\le 1 \ \rho
?1≤ρ≤1?ρ接近+1时正相关较强,接近-1时负相关较强,等于0则没有关系,因此更容易用它比较关系强度
#python计算相关系数用numpy.corrcoef()
x=np.array([50,70,40,60,80])
y=np.array([60,80,50,50,70])
print("---使用corrcoef()函数---")
print(np.corrcoef(x,y))
print()
print("---根据协方差与标准差进行计算")
cov_xy=np.average((x-np.average(x))*(y-np.average(y)))
print(cov_xy/(np.std(x)*np.std(y)))
plt.scatter(x,y)
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
---使用corrcoef()函数---
[[1. 0.72760688]
[0.72760688 1. ]]
---根据协方差与标准差进行计算
0.7276068751089989
条件概率和贝叶斯定理
条件概率
表示事件B发生时A发生的概率
P
(
A
∣
B
)
=
P
(
A
∩
B
)
P
(
B
)
P(A\mid B)=\frac{P(A\cap B)}{P(B)}
P(A∣B)=P(B)P(A∩B)?
其中
P
(
A
∩
B
)
P(A\cap B)
P(A∩B)是A、B同时发生的概率
举例:袋子里5个黑球,5个白球;白球中3个写0,2个写1;黑球中2个写0,3个写1
则摸到白0的概率是?
计摸到0是A事件,是白球是B事件
P
(
A
∣
B
)
=
P
(
A
∩
B
)
P
(
B
)
P(A\mid B)=\cfrac{P(A\cap B)}{P(B)}
P(A∣B)=P(B)P(A∩B)?
P
(
A
∩
B
)
=
3
10
P(A\cap B)=\cfrac{3}{10}
P(A∩B)=103? ,
P
(
B
)
=
1
2
P(B)=\cfrac{1}{2}
P(B)=21?,则
P
(
A
∣
B
)
=
3
10
1
2
=
3
5
P(A\mid B)=\cfrac{\cfrac{3}{10}}{\cfrac{1}{2}}=\cfrac{3}{5}
P(A∣B)=21?103??=53?
贝叶斯定理
公式如下:
P
(
B
∣
A
)
=
P
(
A
∣
B
)
P
(
B
)
P
(
A
)
P(B\mid A)=\cfrac{P(A\mid B)P(B)}{P(A)}
P(B∣A)=P(A)P(A∣B)P(B)?
其中
P
(
B
)
P(B)
P(B)为先验概率,
P
(
B
∣
A
)
P(B\mid A)
P(B∣A)是B发生在A之后称为后验概率,即该公式就是将先验概率转换为后验概率
推导过程:
∵
?
P
(
A
∩
B
)
=
P
(
B
∩
A
)
∴
P
(
B
∣
A
)
=
P
(
B
∩
A
)
P
(
A
)
两
边
同
时
除
以
P
(
A
∣
B
)
=
P
(
A
∩
B
)
P
(
B
)
?
P
(
B
∣
A
)
P
(
A
∣
B
)
=
P
(
B
)
P
(
A
)
?
P
(
B
∣
A
)
=
P
(
A
∣
B
)
P
(
B
)
P
(
A
)
\because \ P(A\cap B)=P(B\cap A) \\ \therefore P(B\mid A)=\cfrac{P(B\cap A)}{P(A)}两边同时除以P(A\mid B)=\cfrac{P(A\cap B)}{P(B)}\\ \Rightarrow \cfrac{P(B\mid A)}{P(A\mid B)}=\cfrac{P(B)}{P(A)}\Rightarrow P(B\mid A)=\cfrac{P(A\mid B)P(B)}{P(A)}
∵?P(A∩B)=P(B∩A)∴P(B∣A)=P(A)P(B∩A)?两边同时除以P(A∣B)=P(B)P(A∩B)??P(A∣B)P(B∣A)?=P(A)P(B)??P(B∣A)=P(A)P(A∣B)P(B)?
似然
n个元素构成的数据
x
1
,
x
2
,
?
?
,
x
n
x_1,x_2,\cdots,x_n
x1?,x2?,?,xn?
这些值出现的概率为:
p
(
x
1
)
,
p
(
x
2
)
,
?
?
,
p
(
x
n
)
p(x_1),p(x_2),\cdots,p(x_n)
p(x1?),p(x2?),?,p(xn?)
则似然表达式:
p
(
x
1
)
p
(
x
2
)
?
p
(
x
n
)
=
∏
k
=
1
n
p
(
x
k
)
p(x_1)p(x_2)\cdots p(x_n)=\prod_{k=1}^{n}p(x_k)
p(x1?)p(x2?)?p(xn?)=k=1∏n?p(xk?)
若使用正态分布概率密度函数
p
(
x
)
=
1
σ
2
π
exp
?
(
?
(
x
?
μ
)
2
2
σ
2
)
p(x)=\cfrac{1}{\sigma\sqrt{2\pi}}\exp\big( -\cfrac{(x-\mu)^2}{2\sigma^2} \big)
p(x)=σ2π?1?exp(?2σ2(x?μ)2?)
则可用概率密度函数将似然表达如下
L
=
∏
k
=
1
n
p
(
x
k
)
=
(
1
σ
2
π
)
n
∏
k
=
1
n
exp
?
(
?
(
x
k
?
μ
)
2
2
σ
2
)
=
(
1
σ
2
π
)
n
∏
k
=
1
n
exp
?
(
?
∑
k
=
1
n
(
x
k
?
μ
)
2
2
σ
2
)
L=\prod_{k=1}^np(x_k)=\big( \cfrac{1}{\sigma\sqrt{2\pi}} \big)^n\prod_{k=1}^n\exp\big( -\cfrac{(x_k-\mu)^2}{2\sigma^2} \big)\\=\big( \cfrac{1}{\sigma\sqrt{2\pi}} \big)^n\prod_{k=1}^n\exp(-\sum\limits_{k=1}^n\cfrac{(x_k-\mu)^2}{2\sigma^2})
L=k=1∏n?p(xk?)=(σ2π?1?)nk=1∏n?exp(?2σ2(xk??μ)2?)=(σ2π?1?)nk=1∏n?exp(?k=1∑n?2σ2(xk??μ)2?)
而似然是概率之积,若放置不管结果会无限趋于0,同时难以进行微分,所以常用对数形式来处理似然,则上式可表示为
log
?
L
=
∑
k
=
1
n
log
?
p
(
x
k
)
=
n
log
?
(
1
σ
2
π
)
?
∑
k
=
1
n
(
x
k
?
μ
)
2
2
σ
2
\log{L}=\sum\limits_{k=1}^n\log p(x_k)=n\log{\big( \cfrac{1}{\sigma\sqrt{2\pi}} \big)}-\sum\limits_{k=1}^n \cfrac{(x_k-\mu)^2}{2\sigma^2}
logL=k=1∑n?logp(xk?)=nlog(σ2π?1?)?k=1∑n?2σ2(xk??μ)2?
import numpy as np
import matplotlib.pyplot as plt
#画出数据在x轴上的散点图
x_data=np.array([2.4,1.2,3.5,2.1,4.7])
y_data=np.zeros(5)
#假定mu和sigma
mu=0
sigma=1
#正态分布密度函数
def pdf(x,mu,sigma):
return 1/(sigma*np.sqrt(2*np.pi))*np.exp(-((x-mu)**2)/(2*sigma**2))
x_pdf=np.linspace(-5,5)
y_pdf=pdf(x_pdf,mu,sigma)
plt.scatter(x_data,y_data)
plt.plot(x_pdf,y_pdf)
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
#求似然
print("---似然---")
print(np.prod(pdf(x_data,mu,sigma)))
print("---对数似然---")
print(np.sum(np.log(pdf(x_data,mu,sigma))))
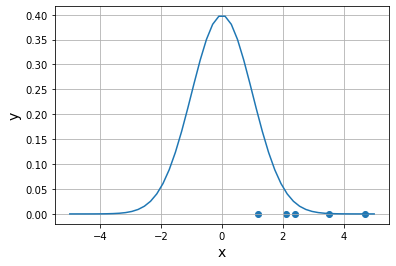
---似然---
1.0632480805734735e-12
---对数似然---
-27.569692666023364
import numpy as np
import matplotlib.pyplot as plt
#画出数据在x轴上的散点图
x_data=np.array([2.4,1.2,3.5,2.1,4.7])
y_data=np.zeros(5)
#假定mu和sigma
mu=np.average(x_data)
sigma=np.std(x_data)
#正态分布密度函数
def pdf(x,mu,sigma):
return 1/(sigma*np.sqrt(2*np.pi))*np.exp(-((x-mu)**2)/(2*sigma**2))
x_pdf=np.linspace(-3,7)
y_pdf=pdf(x_pdf,mu,sigma)
plt.scatter(x_data,y_data)
plt.plot(x_pdf,y_pdf)
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
#求似然
print("---似然---")
print(np.prod(pdf(x_data,mu,sigma)))
print("---对数似然---")
print(np.sum(np.log(pdf(x_data,mu,sigma))))
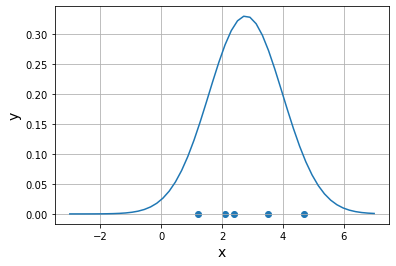
---似然---
0.0003211757807192693
---对数似然---
-8.043521981227514
#通过图像来确认假设为正太分布时的最大似然
x_data=np.array([2.4,1.2,3.5,2.1,4.7])
mu=np.average(x_data)
sigma=np.std(x_data)
def pdf(x,mu,sigma):
return 1/(sigma*np.sqrt(2*np.pi))*np.exp(-(x-mu)**2/(2*sigma**2))
#对数似然函数
def log_likelihood(p):
return np.sum(np.log(p))
x_sigma=np.linspace(0.5,8)#通过调整标准差找到最大似然
y_loglike=[]#记录随着x_sigma增大的对数似然值
for s in x_sigma:
log_like=log_likelihood(pdf(x_data,mu,s))
y_loglike.append(log_like)
plt.plot(x_sigma,np.array(y_loglike))
#画曲线的另一种方式传入([x1,x2],[y1,y2])
plt.plot([sigma,sigma],[min(y_loglike),max(y_loglike)],linestyle="dashed")#画得到最大似然时的x=sigma垂线
plt.xlabel("x_sigma",size=14)
plt.ylabel("y_loglike",size=14)
plt.grid()
plt.show()
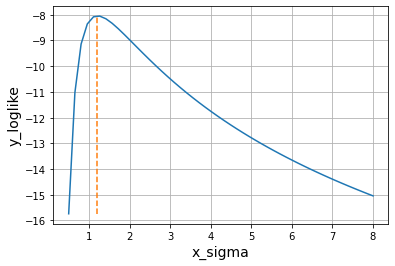
信息量
选择信息量(自熵)
事件E发生的概率为
P
(
E
)
P(E)
P(E),此时它的选择信息量
I
(
E
)
I(E)
I(E)可表示为:
I
(
E
)
=
?
log
?
2
P
(
E
)
I(E)=-\log_{2}P(E)
I(E)=?log2?P(E)
底为2或是其他本质上没有区别
例如:抛一枚硬币正面朝上的概率为
1
2
\frac{1}{2}
21?则它的选择信息量为
?
log
?
2
1
2
=
1
-\log_2\frac{1}{2}=1
?log2?21?=1
选择信息量是衡量某个时间多难发生的尺度,而不是有用性的尺度,例如:中奖概率1/100的奖金是1元还是1亿元它们的信息量并没有区别
#画出0.01到1的选择信息量图表
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(0.01,1)
y=-np.log2(x)
plt.plot(x,y)
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
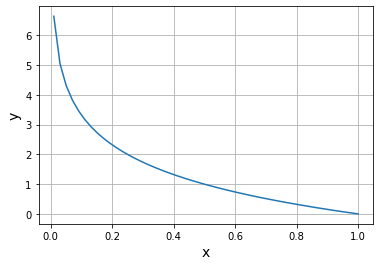
可以发现x趋于0,信息量越大,发生难度越大
信息量有可求和的特性
例如一副扑克牌抽到黑桃1的概率是1/52则信息量为
log
?
2
52
\log_2 52
log2?52,抽到黑桃概率是1/4,抽到1概率是1/13则
log
?
2
4
+
log
?
2
12
=
log
?
2
52
\log_24+\log_212=\log_252
log2?4+log2?12=log2?52,即抽到黑桃与抽到1的选择信息量之和与抽到黑桃1的值完全相等
平均信息量(熵)
又称为香浓信息量
H
=
?
∑
k
=
1
n
P
(
E
k
)
log
?
2
P
(
E
k
)
H=-\sum\limits_{k=1}^nP(E_k)\log_2P(E_k)
H=?k=1∑n?P(Ek?)log2?P(Ek?)
就是选择信息量乘上概率后的总和
例子:抛硬币正面概率为P反面为1-P,则平均信息量为:
H
=
?
P
log
?
2
P
?
(
1
?
p
)
log
?
2
(
1
?
p
)
H=-P\log_2P-(1-p)\log_2(1-p)
H=?Plog2?P?(1?p)log2?(1?p)
画出图像:
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(0.01,0.99)
y=-x*np.log2(x)-(1-x)*np.log2(1-x)
plt.plot(x,y)
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
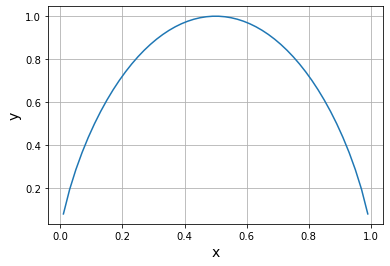
这表明了,越难预测平均信息量越大,越容易预测平均信息量越小,则平均信息量是衡量信息无序性和不确定性的标准。
交叉熵
交叉熵是衡量概率分布与预期值之间距离的尺度
例子:事件发生的概率是P则不发生的概率为1-P,用一个变量t取值为0或1,将该事件的两种情况结合起来
P
(
1
?
P
)
1
?
t
(12-1)
P(1-P)^{1-t}\tag{12-1}
P(1?P)1?t(12-1)
t=1时表示该事件发生的概率,t=0时表示该事件不发生的概率
推广到n个事件并使用似然来得到我们预测的准确程度,这里的
t
k
t_k
tk?就表示事件是否实际发生
L
=
∏
k
=
1
n
P
k
t
k
(
1
?
P
k
)
1
?
t
k
(12-2)
L=\prod_{k=1}^nP_k^{t_k}(1-P_k)^{1-t_k}\tag{12-2}
L=k=1∏n?Pktk??(1?Pk?)1?tk?(12-2)
进一步探究:
假设
P
(
x
)
P(x)
P(x)是我们预测的概率密度函数,可以通过式子
(
12.2
)
(12.2)
(12.2)即事件是否真实发生的似然来判断我们概率密度函数(概率分布)的合理性。
原理:若我们预测的
P
(
x
k
)
P(x_k)
P(xk?)越小则
1
?
P
(
x
k
)
1-P(x_k)
1?P(xk?)一定更大,说明我们认为该事件不发生的概率较大,那么
P
k
t
k
(
1
?
P
k
)
1
?
t
k
P_k^{t_k}(1-P_k)^{1-t_k}
Pktk??(1?Pk?)1?tk?实际上不发生时
t
k
=
0
t_k=0
tk?=0那么就是L式子中乘上了
(
1
?
P
k
)
(1-P_k)
(1?Pk?)相较于乘上较小的
P
k
P_k
Pk?更大了,说明在事件
x
k
x_k
xk?上的预测是正确的,最后得到的
L
L
L也更大,同理
P
k
P_k
Pk?较大时也可证得预测正确时
L
L
L更大。
同样乘积的形式难以微分,用log使其变形为对数形式,并转变正负号:
E
=
?
log
?
L
=
?
∑
k
=
1
n
(
t
k
log
?
P
k
+
(
1
?
t
k
)
log
?
(
1
?
P
k
)
)
(12-3)
E=-\log L=-\sum\limits_{k=1}^n\big( t_k\log P_k+(1-t_k)\log (1-P_k) \big)\tag{12-3}
E=?logL=?k=1∑n?(tk?logPk?+(1?tk?)log(1?Pk?))(12-3)
E就是交叉熵,那么当交叉熵越小概率分布越合理,在人工智能对两个组进行分类时,为了使交叉熵最小,通常会进行训练学习。
有任意一个事件发生的场合
考虑在m个事件中任意一个事件发生时的交叉熵。
P
j
P_j
Pj?为事件j发生的概率则:
∑
j
=
1
m
p
j
\sum\limits_{j=1}^m p_j
j=1∑m?pj?
同样事件j的发生概率可归纳为
∏
j
=
1
m
p
j
t
j
\prod_{j=1}^m p_j^{t_j}
j=1∏m?pjtj??其中
t
j
t_j
tj?表示事件j是否实际发生,因为是m个事件中只有1个发生则
t
1
,
t
2
,
?
?
,
t
m
t_1,t_2,\cdots,t_m
t1?,t2?,?,tm?只有1个为1
那么事件发生n次的似然可以表示为
∏
k
=
1
n
∏
j
=
1
m
p
k
j
t
k
j
\prod_{k=1}^n\prod_{j=1}^m p_{kj}^{t_{kj}}
k=1∏n?j=1∏m?pkjtkj??
取负号和对数之后得交叉熵
E
=
?
∑
k
=
1
n
∑
j
=
1
m
(
t
k
j
log
?
P
k
j
)
(12-4)
E=-\sum\limits_{k=1}^n\sum\limits_{j=1}^m(t_{kj}\log{P_{kj}})\tag {12-4}
E=?k=1∑n?j=1∑m?(tkj?logPkj?)(12-4)
在使用神经网络将对象分类为3个以上时,常将交叉熵最小化来进行学习。可将(12-3)、(12-4)看做预测结果(概率)与实际结果的误差,这种函数叫做误差函数或损失函数。
#计算交叉熵利用公式(12-3)
import numpy as np
delta=1e-7#取一个极小值避免log中出现0,在计算log时要加上该极小值
def cross_entropy(p,t):#交叉熵函数
return -np.sum(t*np.log(p+delta)+(1-t)*np.log(1-p+delta))
#正确答案
t=np.array([1,0,1,1,0,0])
p_1=np.array([0.2,0.8,0.1,0.3,0.9,0.7])#与答案相悖的预测
p_2=np.array([0.7,0.3,0.9,0.8,0.1,0.2])#与正确答案相近的预测
print("-----与正确答案相悖的预测-----")
print(cross_entropy(p_1,t))
print("-----与正确答案相近的预测-----")
print(cross_entropy(p_2,t))
-----与正确答案相悖的预测-----
10.231987952842859
-----与正确答案相近的预测-----
1.3703572638850776