我又来给大家分享PAPER了!!!
今天给大家分享的这篇论文是NIPS’ 2021的一篇Few-Shot增量学习(FSCIL)文章,这篇文章通过固定backbone和prototype得到一个简单的baseline,发现这个baseline已经可以打败当前IL和IFSL的很多SOTA方法,基于此通过借鉴robust optimize的方法,提出了在base training训练时通过flat local minima来对后面的session进行fine-tune novel classes,解决灾难性遗忘问题。
| No. | content |
|---|---|
| PAPER | {NIPS’ 2021} Overcoming Catastrophic Forgetting in Incremental Few-Shot Learning by Finding Flat Minima[1] |
| URL | 论文地址 |
| CODE | 代码地址 |
1.1 Motivation
- 不同于现有方法在学习新任务时尝试克服灾难性遗忘问题,这篇文章提出在训练base classes时就提出策略来解决这个问题。
- 作者提出找到base training function的flat local minima,最小值附近loss小,作者认为base classes分离地更好。(直觉上,flat local minima会比sharp的泛化效果更好,参阅下图[2])
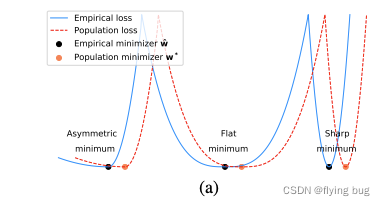
?
1.2 Contribution
- 作者发现一个简单的baseline model,只要在base classes上训练,不在new tasks上进行适应,就超过了现有的SOTA方法,说明灾难性遗忘问题非常严重。
- 作者提出在primitive stage来解决灾难性遗忘问题,通过在base classes上训练时找到flat minima region并在该region内学习新任务,模型能够更好地克服遗忘问题。
?
1.3 A Simple Baseline
作者提出了一个简单的baseline,模型只在base classes上进行训练,在后续的session上直接进行推理。
Training(t=1)
在session 1上对特征提取器进行训练,并使用一个全连接层作为分类器,使用CE Loss作为损失函数,从session 2(
t
≥
2
t\geq2
t≥2)开始将特征提取器固定住,不使用novel classes进行任何fine-tune操作。
Inference(test)
使用均值方式获得每个类的prototype,然后通过欧氏距离
d
(
?
,
?
)
d(·,·)
d(?,?)采用最近邻方式进行分类。分类器的公式如下:
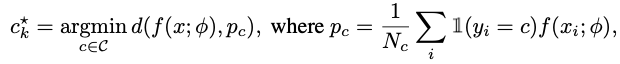
其中
p
c
p_c
pc?表示类别
c
c
c的prototype,
N
c
N_c
Nc?表示类别
c
c
c的训练图片数量。同时作者将
C
T
C^T
CT中所有类的prototypes保存下来用于后续的evaluation。
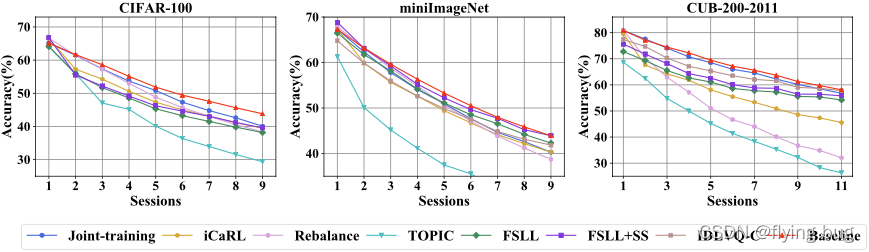
作者表示通过这种保存old prototype的方式就打败了现有的SOTA方法,证明了灾难性遗忘非常严重。
?
1.4 Method
核心想法就是在base training的过程中找到函数的flat local minima
θ
?
\theta^*
θ?,并在后续的few-shot session中在flat region进行fine-tune,这样可以最大限度地保证在novel classes上进行fine-tune时避免遗忘知识。在后续增量few-shot sessions(
t
≥
2
t\geq2
t≥2)中,在这个flat region进行fine-tune模型参数来学习new classes
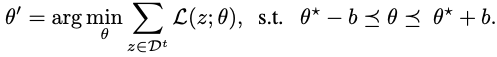
1.4.1 寻找Base Training的flat local minima
Definition 1(
b
b
b-Flat Local Minima) Given a real-valued objective function
L
(
z
;
θ
)
\mathcal{L}(z; θ)
L(z;θ), for any
b
>
0
b > 0
b>0,
θ
?
\theta^*
θ? is a b-flat local minima of
L
(
z
;
θ
)
\mathcal{L}(z; θ)
L(z;θ), if the following conditions are satisfied.
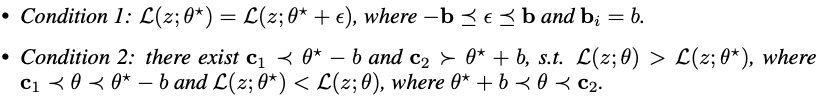
为了找到base training function的近似flat local minima,作者提出添加一些随机噪声到模型参数,噪声可以被多次添加以获得相似但不同的loss function,直觉上,flat local minima附近的参数向量有小的函数值。
假设模型的参数
θ
=
{
?
,
ψ
}
\theta=\{\phi,\psi\}
θ={?,ψ},
?
\phi
?表示特征提取网络的参数,
ψ
\psi
ψ表示分类器的参数。
z
z
z表示一个有类标训练样本,损失函数
L
:
?
R
d
z
→
R
\mathcal{L}:\ \mathbb{R}^{d_z} \rightarrow \mathbb{R}
L:?Rdz?→R。我们的目标就是最小化期望损失函数
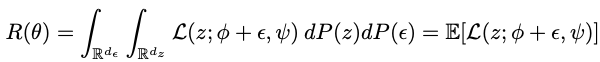
P
(
z
)
P(z)
P(z)是数据分布
P
(
?
)
P(\epsilon)
P(?)是噪声分布,
z
z
z和
?
\epsilon
?是相互独立的。
因此最小化期望损失是不可能的,所以这里我们最小化他的近似,empirical loss,
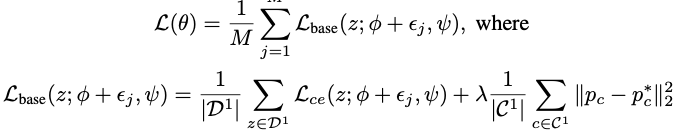
?
i
\epsilon_i
?i?是
P
(
?
)
中
的
噪
声
样
本
P(\epsilon)中的噪声样本
P(?)中的噪声样本,
M
M
M是采样次数。这个loss的前半部分是为了找到flat region,它的特征提取网络参数
?
\phi
?可以很好地区分base classes。第二部分是通过MSE Loss的设计为了让prototype尽量保持不变, 避免模型遗忘过去的知识。
?
1.4.2 在Flat Region内进行IFSL
作者认为虽然flat region很小,但对于few-shot的少量样本来说,足够对模型进行迭代更新。

通过欧氏距离使用基于度量的分类算法来fine-tune模型参数。
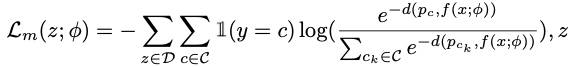
?
1.4.3 收敛性分析
我们的目标是找到一个flat region使模型效果较好。然后,通过最小化期望损失(噪声 ? \epsilon ?和数据 z z z的联合分布)。为了近似这个期望损失,我们在每次迭代中多次从 P ( ? ) P(\epsilon) P(?)采样,并使用随机梯度下降(SGD)优化目标函数。后面是相关的理论证明,感兴趣的可以自行阅读分析。
?
【参考文献】
[1] Shi G, Chen J, Zhang W, et al. Overcoming Catastrophic Forgetting in Incremental Few-Shot Learning by Finding Flat Minima[J]. Advances in Neural Information Processing Systems, 2021, 34.
[2] He H, Huang G, Yuan Y. Asymmetric valleys: Beyond sharp and flat local minima[J]. arXiv preprint arXiv:1902.00744, 2019.