[人工智能]HMM隐马尔科夫模型

隐马尔科夫模型(HMM)

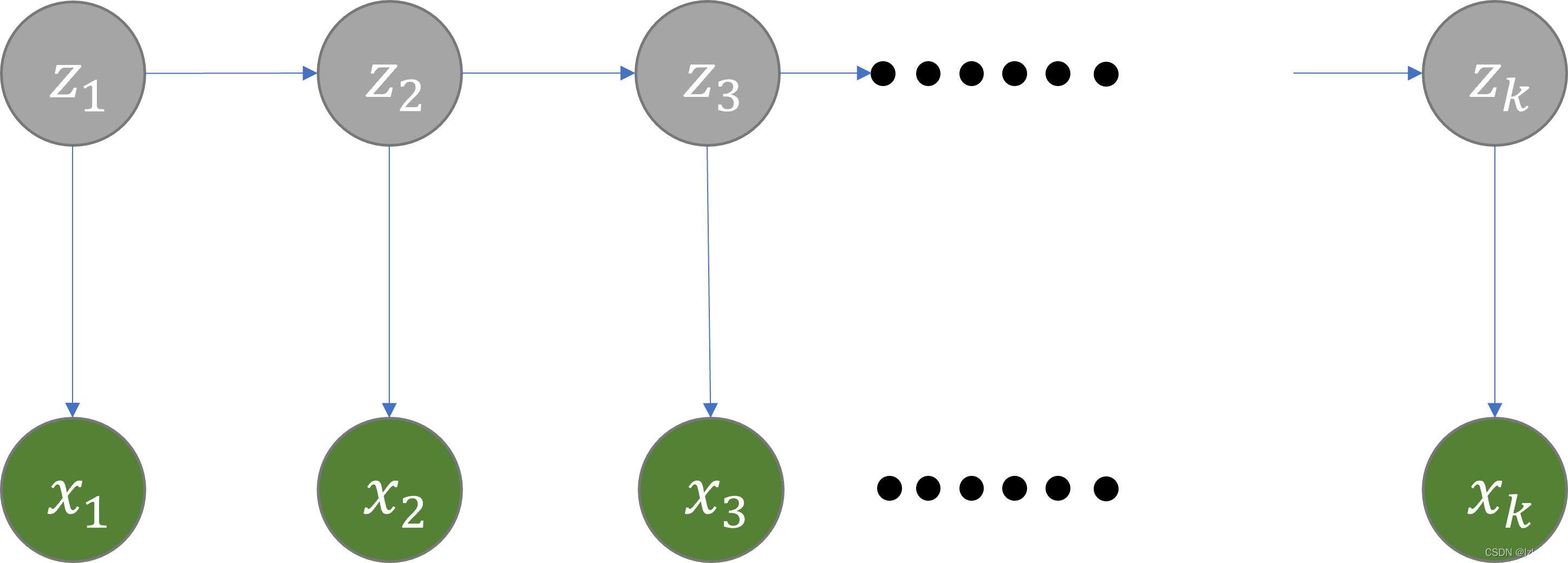
隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，称为状态序列（state sequence)；每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列(observation sequence)。序列的每一个位置又可以看作是一个时刻。

生成式模型vs判别式模型

给定任务：已知序列$x$，求标签$y$，我们要做的实际上就是求$p(Y|X)$

生成式模型

生成式模型是对联合概率$p(x,y)$进行建模，就是考虑所有可能的标签$y$，选择$p(x,y)$?最大的作为输出。

比较常见的生成式模型有：朴素贝叶斯、隐马尔科夫模型等

判别式模型

判别式模型是对条件概率$p(y|x)$进行建模，就是在已知样本集中通过统计或计算得到条件概率，选择$p(y|x)$最大的作为输出。

比较常见的判别式模型有：逻辑回归、条件随机场等

隐马尔可夫模型是一个生成式的模型，即每次给定观测序列，我们考虑所有的标记序列$y$并求出$p(x,y)$，找到使$p(x,y)$最大的$y$?

下面介绍HMM中的三大参数

HMM的参数

HMM模型有三大参数，即$\theta =(\pi ,A,B)$

参数$\pi$

参数$\pi$是一个一维的向量$({\pi }_1,{\pi }_2...{\pi }_n)$，每个元素代表的是状态$i$出现在序列第一个位置的概率。以词性预测为例，$\pi$就表示动词、名词、形容词……出现在句子开头的概率。

参数A

参数$A$也叫transition probability matrix，也就是状态转移概率矩阵。矩阵中每一个元素$A_{ij}$表示从状态$i$转移到状态$j$的概率。

参数B

参数$B$也叫做emission probability matrix，也就是生成概率矩阵。矩阵中每一个元素$B_{ij}$表示状态$i$生成观测值$j$的概率。

下面，我们重点介绍HMM中的三大问题，并对每一个问题做详细探讨。

HMM三大问题

HMM要解决的三大问题如下：

• Inference：在已知模型参数$\theta$和观测序列$x$的前提下，计算概率$p(z_k|x,\theta )$。
• Learning：已知观测序列$x$，求HMM模型参数$\theta =(\pi ,A,B)$
• Decoding：已知模型参数$\theta$和观测序列$x$，求最优的标记序列$z$

Inference

首先介绍Inference问题，也就是在已知模型参数$\theta$?????和观测序列$x$?????的前提下，计算概率$p(z_k|x,\theta )$???????。最简单粗暴的方法是枚举所有可能的状态序列，再进行计算，但显然这个复杂度是指数级别的，不可取。根据条件概率公式，$p(z_k|x,\theta )=\frac{p(z_k,x|\theta )}{p(x|\theta )}$???，也就是说$p(z_k|x,\theta )\propto p(z_k,x|\theta )$???。而$p(z_k,x)=p(x_{1:k},z_k)p(x_{k+1:n}|z_k,x_{1:k})$??。因此，我们介绍两种重要算法来解决这一问题，即Forward和Backward算法，这两个算法的本质都是动态规划(DP)。

前向算法(Forward Algorithm)

前向算法计算的是$p(x_{1:k},z_k|\theta )$??。首先，我们尝试找到递推关系
$$p(x_{1:k},z_k|\theta )=C?p(x_{1:k?1},z_{k?1}|\theta )$$
这里的$C$是我们要找的一个式子。这里可以看到有一个$z_{k?1}$项，因此我们可以尝试引入$z_{k?1}$并把它边缘化，即
$$p(x_{1:k},z_k|\theta )=\sum _{z_{k?1}}p(z_{k?1},z_k,x_{1:k})$$
接着我们对式子进行一个拆分得到
$$\sum _{z_{k?1}}p(z_{k?1},z_k,x_{1:k})=\sum _{z_{k?1}}p(z_{k?1},z_k,x_{1:k?1},x_k)$$

$$\sum _{z_{k?1}}p(z_{k?1},z_k,x_{1:k?1},x_k)=\sum _{z_{k?1}}p(x_{1:k?1},z_{k?1})p(z_k|x_{1:k?1},z_{k?1})p(x_k|z_k,z_{k?1},x_{1:k?1})$$

根据D-Separation我们知道上式可以改写为
$$\sum _{z_{k?1}}p(x_{1:k?1},z_{k?1})p(z_k|x_{1:k?1},z_{k?1})p(x_k|z_k,z_{k?1},x_{1:k?1})=\sum _{z_{k?1}}p(x_{1:k?1},z_{k?1})p(z_k|z_{k?1})p(x_k|z_k)$$
于是，我们成功的找到了这个递推关系。定义${\alpha }_t(i)$?表示$1$到$t$?时刻状态$z_t=i$?的前向概率，递推公式为
$${\alpha }_t(j)=[\sum _i^N{\alpha }_{t?1}(i)A_{ij}]B_{j,x_k}$$
初始状态为${\alpha }_1(i)={\pi }_i{B}_{i,x_1}$

后向算法(Backward Algorithm)

后向算法要计算的是$p(x_{k+1:n}|z_k,\theta )$?，其推导过程与前向算法一样，只是递推的方向不同。
$$p(x_{k+1:n}|z_k)=\sum _{z_{k+1}}p(x_{k+1:n},z_{k+1}|z_k)$$

$$\sum _{z_{k+1}}p(x_{k+1:n},z_{k+1}|z_k)=\sum _{z_{k+1}}p(z_{k+1}|z_k)p(x_{k+1}|z_k,z_{k+1})p(x_{k+2:n}|z_k,z_{k+1},x_{k+1})$$

$$\sum _{z_{k+1}}p(z_{k+1}|z_k)p(x_{k+1}|z_k,z_{k+1})p(x_{k+2:n}|z_k,z_{k+1},x_{k+1})=\sum _{z_{k+1}}p(z_{k+1}|z_k)p(x_{k+1}|z_{k+1})p(x_{k+2:n}|z_{k+1})$$

定义${\beta }_t(i)$??表示$t$?到$n$?，$t$?时刻状态为$z_t=i$??的后向概率，递推公式为
$${\beta }_t(i)=\sum _j^n{A}_{ij}{B}_{j,x_{t+1}}{\beta }_{t+1}(j)$$
初始状态为${\beta }_T(i)=1$

有了前向算法和后向算法，我们的$p(z_k|x)$就可以进行计算，之前我们得到$p(z_k|x)\propto p(x_{1:k},z_k)p(x_{k+1:n}|z_k,x_{1:k})$，根据前向后向算法，$p(z_k=i|x)\propto {\alpha }_k(i){\beta }_k(i)$?。由于是概率，所以我们做一个归一化，也就是
$$p(z_k=i|x)=\frac{{\alpha }_k(i){\beta }_k(i)}{{\sum }_j{\alpha }_k(j){\beta }_k(j)}$$
我们把这个概率用${\gamma }_k(i)$来表示

根据前向向量和后向向量，我们可以再一个概率
$${\xi }_k(i,j)=p(z_k=i,z_{k+1}=j|x,\theta )=\frac{p(z_k=i,z_{k+1}=j,x|\theta )}{p(x|\theta )}$$

$$p(x|\theta )=\sum _i^n\sum _j^{n}p(z_k=i,z_{k+1}=j,x|\theta )$$

$$p(z_k=i,z_{k+1}=j,x|\theta )={\alpha }_k(i)A_{ij}{B}_{j,x_{k+1}}{\beta }_{k+1}(j)$$

于是，
$${\xi }_k(i,j)=\frac{{\alpha }_k(i)A_{ij}{B}_{j,x_{k+1}}{\beta }_{k+1}(j)}{{\sum }_i^n{\sum }_j^n{\alpha }_k(i)A_{ij}{B}_{j,x_{k+1}}{\beta }_{k+1}(j)}$$

Learning

学习问题也就是参数估计问题。对于状态$z$序列已知的情况(complete case)，我们只需要对数据集进行统计即可，类似于N-gram模型。但是在HMM中，我们的状态序列是未知的，这也就是为什么被叫做隐马尔科夫模型。对于这种情况(incomplete case)，我们采用的方法叫做EM算法

EM算法

EM算法全称叫做Expectation Maximization algorithm，专门用于求解含有$latent$ $variable$?的模型参数。EM算法的流程如下：

1. 设置模型参数的初始值${\theta }_0$
2. E步：将模型参数初始值视为已知量，根据第$i$次迭代的模型参数${\theta }_i$求第$i+1$步状态序列$z$?的期望
3. M步：求使得E步求出的期望最大的模型参数${\theta }_{i+1}$?作为第$i+1$次迭代的模型参数估计值
4. 迭代，直至收敛

参数$\pi$求解

$\pi =({\pi }_1,{\pi }_2......{\pi }_n)$?表示每一种状态作为初始状态的概率。由Inference问题我们可以求出$p(z_k|x)$?，我们可以把这个概率当作是$\pi$?的一个期望值。于是套用EM算法即可。期望计算公式为
$${\pi }_i^{(n+1)}={\gamma }_1(i)$$

参数A求解

参数$A$是转移概率矩阵，每个元素$A_{ij}$的概率表达为$p(z_k=i,z_{k+1}=j|x)$。而这个概率是我们之前求出的${\xi }_k(i,j)$?。这个概率也可以被视作是一个期望值，于是可以使用EM算法。期望计算公式为
$$A_{ij}^{(n+1)}=\frac{{\sum }_{t=1}^{T?1}{\xi }_t(i,j)}{{\sum }_{t=1}^{T?1}{\gamma }_t(i)}$$

参数B求解

参数B是生成概率矩阵，?同理，期望计算公式为
$$B_{i,x_t}^{(n+1)}=\frac{{\sum }_{t=1,x_t=k}^T{\gamma }_t(i)}{{\sum }_{t=1}^T{\gamma }_t(i)}$$

Decoding

预测问题也被称为解码问题，就是已知观测序列和模型参数，来预测最优的标记序列。最笨的办法是枚举出所有可能的状态序列，然后找概率最大的，但复杂度显然是不可接受的。

下面介绍Viterbi算法。维特比算法本质是一种动态规划算法，它的计算原理可以通过下图来理解

Viterbi算法其实就是在寻找一条最优的路径，那么在HMM问题中，就是找一条概率最大的路径。

定义${\delta }_k(i)$表示到第$k$时刻，$z_k=i$的最优路径，递推公式如下
$${\delta }_{k+1}(j)=ma{x}_{i=(1,2,3...n)}({\delta }_k(i)A_{ij}{B}_{i,x_{k+1}})$$
初始条件为
$${\delta }_1(i)={\pi }_i{B}_{i,x_1}$$
由于涉及到概率相乘，我们也可以把$\delta$?定义在对数空间，那么递推式为
δ k + 1 ( j ) = m a x i = ( 1 , 2 , 3... n ) { δ k ( i ) + l o g ( A i j ) + l o g ( B j , x k + 1 ) } \delta_{k+1}(j)=max_{i=(1,2,3...n)}\lbrace\delta_{k}(i)+log(A_{ij}) + log(B_{j,x_{k+1}})\rbrace δk+1?(j)=maxi=(1,2,3...n)?{δk?(i)+log(Aij?)+log(Bj,xk+1??)}

$${\delta }_1(i)=log{\pi }_i+log{B}_{i,x_1}$$

算法复杂度是$O(n^{2}m)$?

以把$\delta$?定义在对数空间，那么递推式为
δ k + 1 ( j ) = m a x i = ( 1 , 2 , 3... n ) { δ k ( i ) + l o g ( A i j ) + l o g ( B j , x k + 1 ) } \delta_{k+1}(j)=max_{i=(1,2,3...n)}\lbrace\delta_{k}(i)+log(A_{ij}) + log(B_{j,x_{k+1}})\rbrace δk+1?(j)=maxi=(1,2,3...n)?{δk?(i)+log(Aij?)+log(Bj,xk+1??)}

$${\delta }_1(i)=log{\pi }_i+log{B}_{i,x_1}$$

算法复杂度是$O(n^{2}m)$?

至此，HMM模型的内容就介绍完了，这个模型的原理较为复杂，要勤复习。