为什么要进行信道估计?
信号在通过信道传输的时候,会受到信道中种种因素产生的噪声以及可能发生的多径效应,弄清信号经过的信道的特性,表征信道的技术/过程称为信道估计(Channel Estimation)。
注:attenuate(减弱);phase-shift(相位移动);add noise(噪声)
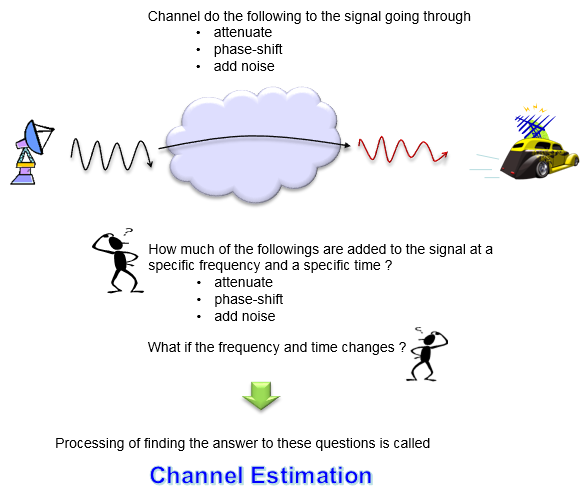
上图中的诉求,就是信道估计的目的。
如何信道估计?
我们知道了为什么要进行信道估计,接下来的问题就是我们如何找出信道的属性来估计信道?有许多不同的信道估计的方法,但是基本的思想大同小异,步骤如下:
- 1、使用信道矩阵来建立一个传输信号和接收信号的数学模型
- 2、传输一个已知的信号然后检测收到的信号,同城这个已知的信号被称为参考信号(Reference signal)
- 3、通过对比传输信号和接收信号,我们可以求解信道矩阵的元素
生成算法
我们该如何算出信道的特性呢?
- 1、我们输入了一组预定义的信号,也就是参考信号。
- 2、当这些参考信号通过信道时,它开始变形(衰减,相移,被加以噪声)
- 3、我们在接收方检测和解码接收到的参考信号
- 4、比较发送的参考信号和接收的参考信号,并找到它们之间的相关性。
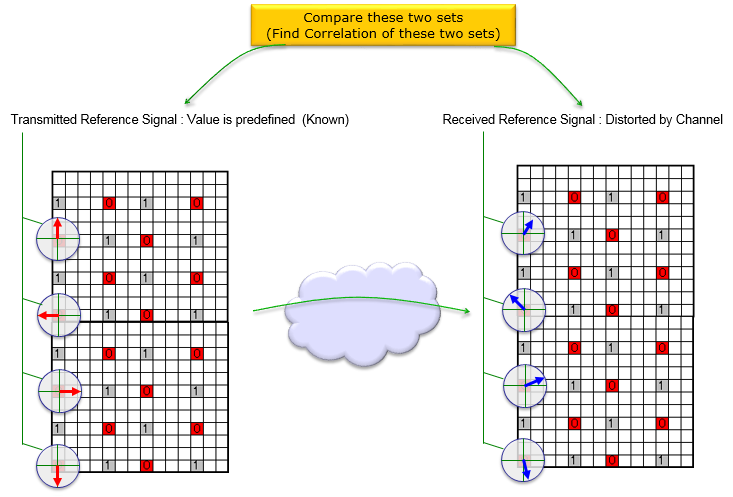
对 2 × 2 2\times2 2×2 MIMO 二输入二输出信道进行信道估计
对信道进行建模
我们假定有一个通信系统如下图所示,
x
(
t
)
x(t)
x(t)表示发送信号,
y
(
t
)
y(t)
y(t)表示接收信号。当
x
(
t
)
x(t)
x(t)在信道中传输时,它会变形、被加以各种噪声
n
n
n,并且可能会相互干扰。因此接收到的信号
y
(
t
)
y(t)
y(t)与发送信号
x
(
t
)
x(t)
x(t)不同。
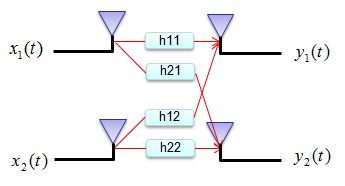
发射信号,接收信号和信道矩阵之间的关系建立数学模型,如下式:
[
y
1
(
t
)
y
2
(
t
)
]
=
[
h
11
h
12
h
21
h
22
]
[
x
1
(
t
)
x
2
(
t
)
]
+
[
n
1
n
2
]
\begin{bmatrix} y_{1}(t) \\ y_{2}(t) \end{bmatrix} = \begin{bmatrix}h_{11} & h_{12} \\ h_{21} & h_{22}\end{bmatrix}\begin{bmatrix} x_{1} (t)\\x_{2}(t) \end{bmatrix}+\begin{bmatrix} n_{1} \\ n_{2}\end{bmatrix}
[y1?(t)y2?(t)?]=[h11?h21??h12?h22??][x1?(t)x2?(t)?]+[n1?n2??]
在此等式中,我们已知
x
1
(
t
)
x_{1}(t)
x1?(t)和
x
2
(
t
)
x_{2}(t)
x2?(t),也就是传输信号或参考信号,同时已知
y
1
(
t
)
y_{1}(t)
y1?(t)和
y
2
(
t
)
y_{2}(t)
y2?(t),也就是接收信号,我们不知道的部分就是信道矩阵
H
H
H和噪声
n
1
、
n
2
n_1 、n_2
n1?、n2?。
求解部分
为了简化模型,我们假定信道没有噪声,也就是**
n
1
、
n
2
n_1 、n_2
n1?、n2?置零**。由于我们有数学模型,因此下一步是传输信号(参考信号)并从参考信号中求解出信道参数。
假设我们仅通过一个天线发送了幅度为1的已知信号,而另一个天线现在处于关闭状态。假设第一个天线接收幅度为0.8的参考信号,第二个天线接收幅度为0.2的参考信号,我们可以得出如下所示的一行信道矩阵
H
H
H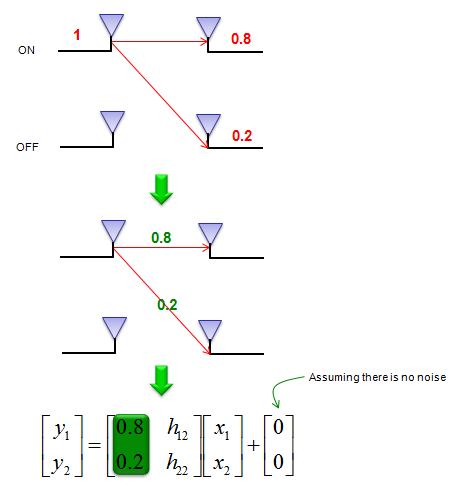
假设我们仅通过另一个天线发送了幅度为1的已知信号,并且第一个天线现在处于关闭状态,假设第一个天线接收到幅度为0.3的参考信号,第二个天线接收到幅度为0.7的参考信号。有了这个结果,我们可以得出如下所示的一行信道矩阵
H
H
H。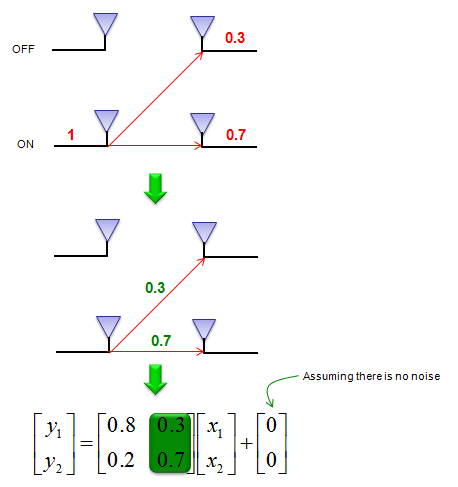
此简化模型便于理解,但如果完全按照上述方法,则会导致效率低下。根据上述,应该有一个时刻,仅发送参考信号而没有实际数据,只是为了估计信道信息,这意味着由于信道估计过程的存在,数据速率将降低。为了消除这种效率低下的问题,实际的通信系统会同时发送参考信号和数据。
我们的问题转化为:如何在同时传输参考信号和数据的情况完成信道估计?
如何在同时传输参考信号和数据的情况完成信道估计?
以 LTE为例,我们使用如下图所示的方法。在 LTE 中为
2
×
2
2 \times 2
2×2 MIMO的情况下,每个子帧都留有给每个天线的参考信号的不同位置。天线0的子帧发送了分配给天线0的参考信号,不发送分配给天线1的任何信号。天线1的子帧发送了分配给天线1的参考信号的信号,不发送分配给天线0的任何信号。因此,如果在两个接收器天线上解码为天线0的参考信号分配的资源元素,则可以估计
h
11
,
h
12
h11,h12
h11,h12。(此时依旧假设没有噪音)。如果在两个接收器天线上解码分配给天线1参考信号的资源元素,则可以估计
h
21
,
h
22
h21,h22
h21,h22。
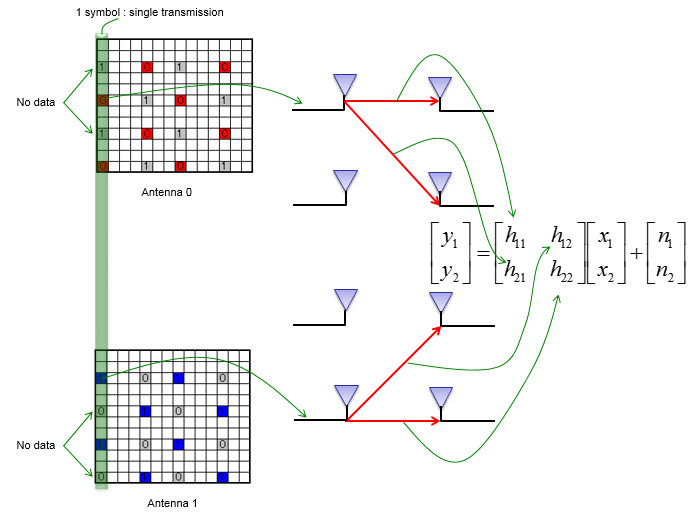
信道系数的估计
上面说明的过程是针对LTE OFDMA符号中的频域中的一个特定点测量
H
H
H矩阵,如果使用求解得
H
H
H矩阵的方法,对信道等式其他符号承参数进行解码,则解码的符号的准确性可能不尽人意,因为上一步中使用的测量数据会包含一定程度的噪声。
因此,在实际应用中,对通过上述方法测得的
H
H
H矩阵的值进行某种处理,在此处理过程中,我们可以找出噪声的总体统计属性(例如,噪声的均值,方差和统计分布),而在此过程中获得的特定噪声值本身并没有太多意义。从参考信号获得的特定值将与用于解码其他数据的噪声值(非参考信号)不同,因为噪声值是随机变化的。然而,那些随机噪声的总体特性可以是重要的信息(例如,在SNR估计等中使用)
我们将系统方程式描述如下,其中包括噪声项,但这并不意味着您可以直接测量噪声。是不可能的。该方程式仅表明检测到的信号
y
y
y 包含噪声分量的某些部分。
[
y
1
(
t
)
y
2
(
t
)
]
=
[
h
11
h
12
h
21
h
22
]
[
x
1
(
t
)
x
2
(
t
)
]
+
[
n
1
n
2
]
\begin{bmatrix} y_{1}(t) \\ y_{2}(t) \end{bmatrix} = \begin{bmatrix}h_{11} & h_{12} \\ h_{21} & h_{22}\end{bmatrix}\begin{bmatrix} x_{1} (t)\\x_{2}(t) \end{bmatrix}+\begin{bmatrix} n_{1} \\ n_{2}\end{bmatrix}
[y1?(t)y2?(t)?]=[h11?h21??h12?h22??][x1?(t)x2?(t)?]+[n1?n2??]
因此,当我们测量信道系数时,我们假定没有噪声项,如下式子
[
y
1
(
t
)
y
2
(
t
)
]
=
[
h
11
h
12
h
21
h
22
]
[
x
1
(
t
)
x
2
(
t
)
]
\begin{bmatrix} y_{1}(t) \\ y_{2}(t) \end{bmatrix} = \begin{bmatrix}h_{11} & h_{12} \\ h_{21} & h_{22}\end{bmatrix}\begin{bmatrix} x_{1} (t)\\x_{2}(t) \end{bmatrix}
[y1?(t)y2?(t)?]=[h11?h21??h12?h22??][x1?(t)x2?(t)?]
在LTE的特定应用中,我们在OFDM符号中有多个测量点(多个参考信号)。这些测量点在频域上表示。因此,重写信道矩阵以指示每个信道矩阵的测量点。
H
(
f
0
)
=
[
h
(
f
)
11
h
(
f
)
12
h
(
f
)
21
h
(
f
)
22
]
H(f_0) = \begin{bmatrix}h(f)_{11} & h(f)_{12} \\ h(f)_{21} & h(f)_{22}\end{bmatrix}
H(f0?)=[h(f)11?h(f)21??h(f)12?h(f)22??]
假设已经测量了整个OFDM符号上的
H
H
H矩阵,如下所示,每个矩阵都以一个特定的频率指示
H
H
H矩阵
H
(
f
0
)
=
[
h
(
f
)
11
h
(
f
)
12
h
(
f
)
21
h
(
f
)
22
]
H
(
f
1
)
=
[
h
(
f
)
11
h
(
f
)
12
h
(
f
)
21
h
(
f
)
22
]
?
H
(
f
n
?
1
)
=
[
h
(
f
)
11
h
(
f
)
12
h
(
f
)
21
h
(
f
)
22
]
H
(
f
n
)
=
[
h
(
f
)
11
h
(
f
)
12
h
(
f
)
21
h
(
f
)
22
]
H(f_0) = \begin{bmatrix}h(f)_{11} & h(f)_{12} \\ h(f)_{21} & h(f)_{22}\end{bmatrix}\\ \quad\\ H(f_1) = \begin{bmatrix}h(f)_{11} & h(f)_{12} \\ h(f)_{21} & h(f)_{22}\end{bmatrix}\\ \vdots \\ H(f_{n-1}) = \begin{bmatrix}h(f)_{11} & h(f)_{12} \\ h(f)_{21} & h(f)_{22}\end{bmatrix}\\ \quad\\ H(f_{n}) = \begin{bmatrix}h(f)_{11} & h(f)_{12} \\ h(f)_{21} & h(f)_{22}\end{bmatrix}
H(f0?)=[h(f)11?h(f)21??h(f)12?h(f)22??]H(f1?)=[h(f)11?h(f)21??h(f)12?h(f)22??]?H(fn?1?)=[h(f)11?h(f)21??h(f)12?h(f)22??]H(fn?)=[h(f)11?h(f)21??h(f)12?h(f)22??]
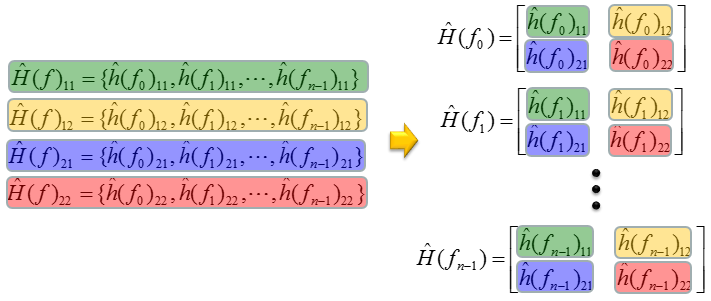
现在你有了一个
H
H
H矩阵数组。该阵列由四个不同的组组成,每个组用不同的颜色突出显示,如下所示。
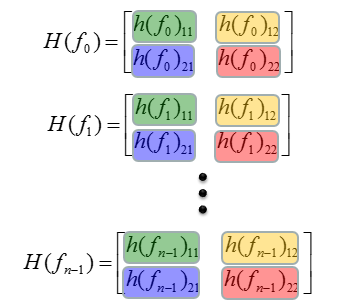
当应用处理算法时,该算法需要分别应用于这些组中的每一个。因此,为简单起见,将
H
H
H矩阵的数组重新排列为多个独立数组(在本例中为4个数组),如下所示
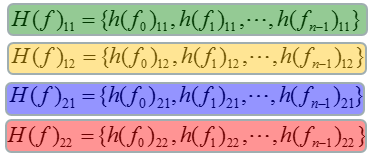
对于每一个数组将进行如下所示的相同处理,有很多处理的方法,但是总体的基本思想都是相似的。对每个频点中的信道系数阵列进行傅里叶变换,将阵列转换到时域上,从而生成标记为(2)的时域数据阵列,实际上,这是特定信道路径的脉冲响应。然后对该时域数据应用特定的过滤(或加窗)。在此示例中,将某个点的数据替换为零,并创建标记为(3)的结果。可以应用更先进复杂的过滤器或窗口,而不是这种简单的调零。然后通过将滤波后的信道脉冲数据转换回频域。此时我们得到了一个信道估计系数,可以用来解码其他信号。
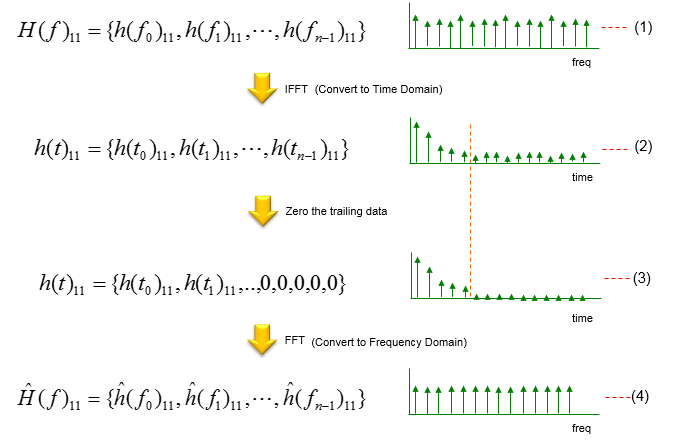
通过对所有四个阵列执行相同的过程,可以获得“估计信道系数阵列”的四个阵列。可以按以下方式重建估计信道矩阵的阵列。
噪声的估计
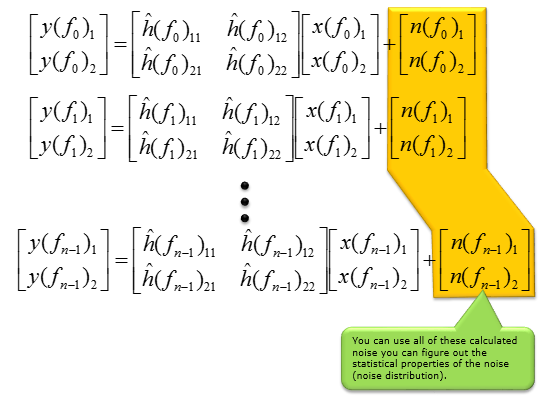
使用此估算的信道矩阵,您可以使用以下公式估算每个点的噪声值。这与本页开头的原始系统方程式相同,除了将
H
H
H矩阵替换为“估计的
H
H
H”矩阵外,现在我们知道除噪声值以外的所有值。因此,通过带入所有已知值,我们可以在每个测量点计算(估计)噪声值。

如果将此方程式应用于所有测量点,则将获得所有测量点的噪声值,并从这些计算出的噪声值中获得噪声的统计属性。如上所述,此处计算出的每个单独的噪声值没有太大意义,因为该值不能直接应用于解码其他信号,但是这些噪声的统计特性对于确定噪声而言可能是非常有用的信息。
参考:http://www.sharetechnote.com/html/Communication_ChannelEstimation.html#General_Algorithm