参考书目:数学教科书,作者:我妻幸长
文章目录
回归与过度学习
回归与分类
模型(用数学公式表示的定量规则)
Y
=
f
(
X
)
Y=f(X)
Y=f(X)来捕捉数据的倾向,
Y
=
{
y
1
,
y
2
,
?
?
,
y
m
}
Y=\{y_1,y_2,\cdots,y_m\}
Y={y1?,y2?,?,ym?},
X
=
{
x
1
,
x
2
,
?
?
,
x
n
}
X=\{x_1,x_2,\cdots,x_n\}
X={x1?,x2?,?,xn?}
若此时Y是连续值,则称为回归,若Y是0、1等离散值则称为分类
多项式回归
可以用求和的方式来表示n次多项式
f
(
x
)
=
∑
k
=
0
n
a
k
x
k
(1-1)
f(x)=\sum\limits_{k=0}^na_kx^k\tag{1-1}
f(x)=k=0∑n?ak?xk(1-1)
此时
a
0
,
a
1
.
?
?
,
a
n
a_0,a_1.\cdots,a_n
a0?,a1?.?,an?是函数的参数
最小二乘法
J
=
∑
j
=
1
m
(
f
(
x
j
)
?
t
j
)
2
(1-2)
J=\sum\limits_{j=1}^m\big( f(x_j)-t_j \big)^2\tag{1-2}
J=j=1∑m?(f(xj?)?tj?)2(1-2)
最小二乘法就是将
J
J
J最小化,求出
f
(
x
)
f(x)
f(x)的参数的方法,其中
t
j
t_j
tj?表示每个数据,通过函数的输出与各项数据相减得出差再求平方和,机器学习中常将此结果乘上1/2后作为误差(为了微分时便于处理)
利用梯度下降法最小化误差
综上我们可以得出线性回归多项式的误差公式
E
=
1
2
∑
j
=
0
m
(
∑
k
=
0
n
a
k
x
j
k
?
t
j
)
2
E=\frac{1}{2}\sum\limits_{j=0}^m\big( \sum\limits_{k=0}^na_kx_j^k -t_j\big)^2
E=21?j=0∑m?(k=0∑n?ak?xjk??tj?)2
即
f
(
x
)
f(x)
f(x)在
x
j
x_j
xj?取
x
1
,
x
2
,
?
?
,
x
m
x_1,x_2,\cdots,x_m
x1?,x2?,?,xm?下对实际值
t
j
t_j
tj?的差做平方的1/2,我们使用梯度下降法调整参数
a
k
a_k
ak?使
E
E
E最小化。
a
i
=
a
i
?
η
?
E
?
a
i
a_i=a_i-\eta\frac{\partial E}{\partial a_i}
ai?=ai??η?ai??E?
其中
0
?
i
?
n
0\leqslant i \leqslant n
0?i?n
此时要求偏微分
?
E
?
a
i
\frac{\partial E}{\partial a_i}
?ai??E?
推导过程
令
u
j
=
∑
k
=
0
n
a
k
x
j
k
?
t
j
?
?
E
?
a
i
=
?
E
?
u
j
?
u
j
?
a
i
=
∑
j
=
0
m
u
j
x
j
i
=
∑
j
=
0
m
(
f
(
x
j
)
?
t
j
)
x
j
i
u_j=\sum\limits_{k=0}^na_kx^k_j-t_j \\ \Rightarrow \cfrac{\partial E}{\partial a_i}=\cfrac{\partial E}{\partial u_j}\cfrac{\partial u_j}{\partial a_i} \\ =\sum\limits_{j=0}^m u_jx_j^i=\sum\limits_{j=0}^m\big( f(x_j)-t_j \big)x_j^i
uj?=k=0∑n?ak?xjk??tj???ai??E?=?uj??E??ai??uj??=j=0∑m?uj?xji?=j=0∑m?(f(xj?)?tj?)xji?
∑
j
=
0
m
u
j
x
j
i
=
∑
j
=
0
m
(
f
(
x
j
)
?
t
j
)
x
j
i
(1-3)
\sum\limits_{j=0}^m u_jx_j^i=\sum\limits_{j=0}^m\big( f(x_j)-t_j \big)x_j^i\tag{1-3}
j=0∑m?uj?xji?=j=0∑m?(f(xj?)?tj?)xji?(1-3)
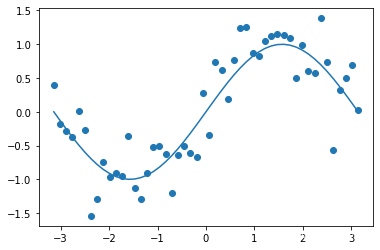
#实验数据的产生
#该数据由sin函数加上噪声
import numpy as np
import matplotlib.pyplot as plt
X=np.linspace(-np.pi,np.pi)
T=np.sin(X)
#画出添加噪声前的图像sin()
plt.plot(X,T)
T+=0.4*np.random.randn(len(X))#len是取X的长度50,生成50个正态分布随机数
plt.scatter(X,T)
plt.show()
X/=np.pi#为方便收敛X限定在-1到1之间,若大于1或小于-1由于x^i可能会很大导致E也很大使得收敛过慢
#实现多项式回归
eta=0.01 #学习系数
#---多项式实现---
def polynomial(x,params):
poly=0
for i in range(len(params)):
poly+=params[i]*x**i
return poly
#求个参数的偏微分(斜率)
def grad_params(X,T,params):
grad_ps=np.zeros(len(params))
for i in range(len(params)):
#偏微分公式
for j in range(len(X)):
grad_ps[i]+=(polynomial(X[j],params)-T[j])*X[j]**i
return grad_ps
#学习
#degree多项式次数,epoch重复次数
def fit(X,T,degree,epoch):
#设定参数初始值
params=np.random.randn(degree+1)#注i次多项式有i+1个参数
#因为x为小数次数越高的参数初始值要越大
for i in range(len(params)):
params[i]*=2**i#用2^i使参数初值增大一些
for i in range(epoch):
#这里python方便的数组操作省去了一个for循环,将所有参数都一起更新
params-=eta*grad_params(X,T,params)
return params
#显示结果
degrees=[1,2,3,4,5,6]#这里测试3个多项式次数分别为1,3,6
for degree in degrees:
print("---"+str(degree)+"次多项式---")
params=fit(X,T,degree,1000)#训练1000次后获取训练后的参数
print(params)
#从训练好的多项式中得到Y轴数组
Y=polynomial(X,params)
plt.scatter(X,T)
plt.plot(X,Y,linestyle="dashed")
plt.show()
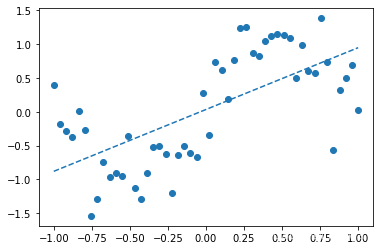
---1次多项式---
[0.0342224 0.9152711]
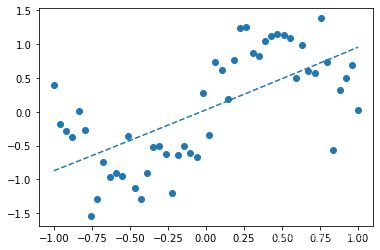
---2次多项式---
[0.03000374 0.9152711 0.01215966]
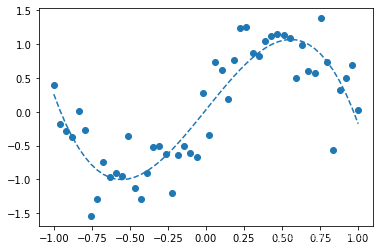
---3次多项式---
[ 0.03000374 2.79869276 0.01215966 -3.01761218]
---4次多项式---
[ 0.31493447 2.79964178 -2.5431648 -3.01905297 2.78197178]
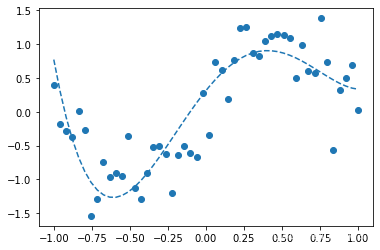
---5次多项式---
[-1.79404683e-02 -3.11067261e+00 3.78078310e-01 2.18767750e+01
-3.66761172e-01 -2.08018029e+01]
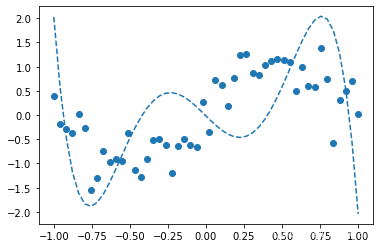
---6次多项式---
[ -0.50409283 3.92572196 11.29919126 -7.97066592 -33.29678186
4.24010247 23.80830819]
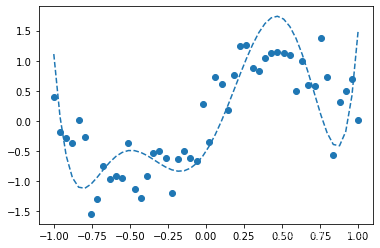
可以看出1次多项式只能大致把握数据趋势,3次多项式函数形状与sin()函数接近,6次多项式发生了过拟合。
过拟合:模型过于复杂等原因而过度拟合数据和适应数据,从而没有抓住数据的本质降低了模型预测未知数据的性能,如6次多项式的预测结果与sin()函数想差较大,应当避免这种问题的发生。
分类与逻辑回归
以0、1等离散值为输出的机器学习模型来捕捉数据的倾向被称为分类
逻辑回归将输入分为0、1二值,例如肿瘤预测根据患者的一些症状表现用
x
i
x_i
xi?表示,1为有症状,0为无症状来作为输入对肿瘤进行预测。
逻辑回归中被用于分类的公式:
y
=
1
1
+
exp
?
(
?
(
∑
k
=
1
n
a
k
x
k
+
b
)
)
(2-1)
y=\cfrac{1}{1+\exp\big( -\big( \sum\limits_{k=1}^na_kx_k+b \big) \big)}\tag{2-1}
y=1+exp(?(k=1∑n?ak?xk?+b))1?(2-1)
令$u= \sum\limits_{k=1}^na_kx_k+b $则上式可写为
y
=
1
1
+
exp
?
(
?
u
)
(2-2)
y=\cfrac{1}{1+\exp(-u)}\tag{2-2}
y=1+exp(?u)1?(2-2)
上式为sigmoid函数,有在
(
0
,
1
)
(0,1)
(0,1)之间连续输出的特性,可以解释为概率,可以使用交叉熵来表示误差
参数优化
使用梯度下降法
a
i
=
a
i
?
η
?
E
?
a
i
b
=
b
?
η
?
E
?
b
(2-3)
a_i=a_i-\eta\frac{\partial E}{\partial a_i}\tag{2-3} \\ b=b-\eta\frac{\partial E}{\partial b}
ai?=ai??η?ai??E?b=b?η?b?E?(2-3)
交叉熵处理误差
E
=
?
∑
j
=
1
m
(
t
j
log
?
y
j
+
(
1
?
t
j
)
log
?
(
1
?
y
j
)
)
(2-4)
E=-\sum\limits_{j=1}^m\big(t_j\log y_j+(1-t_j)\log(1-y_j)\big)\tag{2-4}
E=?j=1∑m?(tj?logyj?+(1?tj?)log(1?yj?))(2-4)
y
j
=
1
1
+
exp
?
(
?
(
∑
k
=
1
n
a
k
x
k
+
b
)
)
(2-5)
y_j=\cfrac{1}{1+\exp\big( -\big( \sum\limits_{k=1}^na_kx_k+b \big) \big)}\tag{2-5}
yj?=1+exp(?(k=1∑n?ak?xk?+b))1?(2-5)
计算偏微分,过程略,计算得:
?
E
?
a
i
=
∑
j
=
1
m
(
y
j
?
t
j
)
x
j
i
(2-6)
\cfrac{\partial E}{\partial a_i}=\sum\limits_{j=1}^m(y_j-t_j)x_{ji}\tag{2-6}
?ai??E?=j=1∑m?(yj??tj?)xji?(2-6)
?
E
?
b
=
∑
j
=
1
m
(
y
j
?
t
j
)
(2-7)
\cfrac{\partial E}{\partial b}=\sum\limits_{j=1}^m(y_j-t_j)\tag{2-7}
?b?E?=j=1∑m?(yj??tj?)(2-7)
生成数据
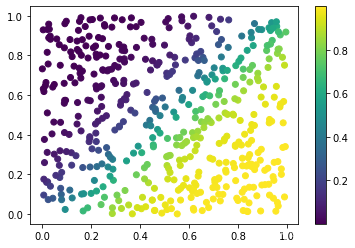
坐标平面的左上方正确标签是0,右下方正确标签是1注:该模型只有x和y两个维度所以是$a_0x_0+a_1x_1+b$
import numpy as np
import matplotlib.pyplot as plt
n_data=500#数据的数量
X=np.zeros((n_data,2))#500行2列的矩阵,第一列为坐标x,第二列为坐标y,也可看做是两个维度x1,x2
T=np.zeros((n_data))#正确的数据标签,用0、1表示
for i in range(n_data):
#随机设定x、y坐标
x_rand=np.random.rand()
y_rand=np.random.rand()
X[i,0]=x_rand
X[i,1]=y_rand
#x比y大即右下角的标签设为1
#使用正态分布使边界模糊
if x_rand>y_rand+0.2*np.random.randn():
T[i]=1
plt.scatter(X[:,0],X[:,1],c=T)#c=1的上色,参数c根据传入的数值0-1变色
plt.colorbar()
plt.show()

实现逻辑回归
#学习系数
eta=0.01
#计算分类,y
def classify(x,a_params,b_param):
#计算∑aixi+b
u=np.dot(x,a_params)+b_param
return 1/(1+np.exp(-u))
#计算交叉熵误差
def corss_entropy(Y,T):
delta=1e-7#极小值防止出现log0
return -np.sum(T*np.log(Y+delta)+(1-T)*np.log(1-Y+delta))
#微分计算
def grad_a_params(X,T,a_params,b_param):
grad_a=np.zeros(len(a_params))
for i in range(len(a_params)):#a_params=2,公式(2-6)
for j in range(len(X)):#len(X)=500
grad_a[i]+=(classify(X[j],a_params,b_param)-T[j])*X[j,i]#X[j]是传入第j行的两个维度
return grad_a
def grad_b_param(X,T,a_params,b_param):
grad_b=0
for i in range(len(X)):
grad_b+=(classify(X[i],a_params,b_param)-T[i])
return grad_b
#学习
#记录误差
error_x=[]
error_y=[]
def fit(X,T,dim,epoch):
#dim是维度,epoch是训练次数
a_params=np.random.randn(dim)
b_param=np.random.randn()
#更新参数
for i in range(epoch):
grad_a=grad_a_params(X,T,a_params,b_param)
grad_b=grad_b_param(X,T,a_params,b_param)
a_params-=eta*grad_a
b_param-=eta*grad_b
Y=classify(X,a_params,b_param)
error_x.append(i)
error_y.append(corss_entropy(Y,T))
return (a_params,b_param)
a_params,b_param=fit(X,T,2,200)
Y=classify(X,a_params,b_param)
#使用模型分类
result_x=[]#x坐标
result_y=[]#y坐标
result_z=[]#概率
for i in range(len(Y)):
result_x.append(X[i, 0])
result_y.append(X[i, 1])
result_z.append(Y[i])
print("---概率分布---")
plt.scatter(result_x,result_y,c=result_z)
plt.colorbar()
plt.show()
#误差变化
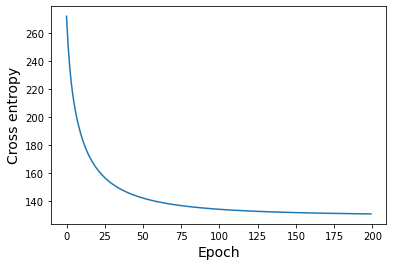
print("---误差的变化---")
plt.plot(error_x,error_y)
plt.xlabel("Epoch",size=14)
plt.ylabel("Cross entropy",size=14)
plt.show()
---概率分布---
---误差的变化---
小结
- 数据分布是根据随机生成的0-1之间的坐标,再通过正态分布模糊边界
- 使用了sigmoid函数和交叉熵得到预测误差E
- 由于数据只有x和y轴维度为2维所以 u = a 0 x 0 + a 1 x 1 + b u=a_0x_0+a_1x_1+b u=a0?x0?+a1?x1?+b通过上面的classify函数实现
- 将误差E求偏微分得到 ? E ? a i \cfrac{\partial E}{\partial a_i} ?ai??E?和 ? E ? b \cfrac{\partial E}{\partial b} ?b?E?再根据梯度下降优化参数降低误差
- 每次优化参数后记录误差
- 根据训练好的参数进行预测分类,用所得概率值使颜色渐变画出分类图像,并画出误差改变的图像
神经网络概述
人工智能、机器学习、神经网络
列举几种与人工智能相关的概念
- 机器学习:计算机算法通过经验进行学习并自动改进,做出判断。
- 遗传算法:模仿进化论,通过组合交叉和变异演算计算模型。
- 群智能:遵循简单规则行动的个体的集合体,以集团形式采取高级的行动。
- 专家系统:模仿人类专家的思维,可以提出基于知识的建议。
- 模糊控制:通过模糊控制规则采取接近人类经验的控制行为。主要用于家电等。
- 强化学习:智能体可以通过反复试验试错,学习如何在环境中实现价值最大化。
- 决策树:通过训练树形结构,可以将数据进行树枝状分类。通过这种方法可以更好地对数据进行预测。
- 支持向量机:训练超平面(平面的扩张),以此来对数据进行分类
- K K K临近:使用最相邻的 K K K个点,通过多数决定进行分类。是最简单的机器学习算法
- 神经网络:以大脑的神经网格为原型构思出的模型,是近年来备受关注的深度学习的基础
神经元模型
在单一神经元中,对多个输入乘以权重并相加然后施加偏置,最后用激活函数进行处理。通过调整每个输入的权重并改变偏置就可以调整进入激活函数的值,偏置可以用来表示神经元灵敏度的值,激活函数就是能令神经元兴奋的函数,根据输入大小决定神经元兴奋程度即是输出。
神经元网络
神经网络是由多个单一神经元组合而成,由多个神经元组成的层经过排列构成。单一神经元可以连接到相邻层中所有的神经元,但不能连接到同一层中的其他神经元。一个神经元的输出是下一层神经元的输入,信息从一层流入下一层。正向传播:将信息从输入流向输出
反向传播(误差传播法):将信息从输出流向输入
通过正向传播从接近输入的层开始逐层处理直到接近输出的层。通过反向传播从接近输出的层接近输入的层并逐层更新权重和偏置。
层数较多的神经网络学习被称为深度学习
学习机制
单一神经元的学习
神经网络通常由具有多个神经元的层组成,为了方便学习使用单一神经元并进行简单的学习。
只有一个输入的神经元,输入为x坐标输出为y坐标。
正向传播表达式
u
=
w
x
+
b
y
=
f
(
u
)
(3-1)
u=wx+b \\ y=f(u)\tag{3-1}
u=wx+by=f(u)(3-1)
其中
w
w
w是权重,
b
b
b是偏置,
f
(
x
)
f(x)
f(x)是激活函数通过该函数得到
y
y
y这里使用sigmoid函数,因此:
y
=
1
1
+
exp
?
(
?
(
w
x
+
b
)
)
y=\cfrac{1}{1+\exp(-(wx+b))}
y=1+exp(?(wx+b))1?
误差(这里处理回归最小二乘,若是处理分类则使用交叉熵):
E
=
1
2
∑
j
=
1
m
(
y
j
?
t
j
)
2
E=\cfrac{1}{2}\sum\limits_{j=1}^m(y_j-t_j)^2
E=21?j=1∑m?(yj??tj?)2
由于是单一神经元所以可以写为
1
2
(
y
?
t
)
2
(3-2)
\cfrac{1}{2}(y-t)^2\tag{3-2}
21?(y?t)2(3-2)
每一次正向传播都求出误差并更新参数,这种学习称为在线学习,若是利用误差的总和对参数进行更新的学习被称为批处理学习。
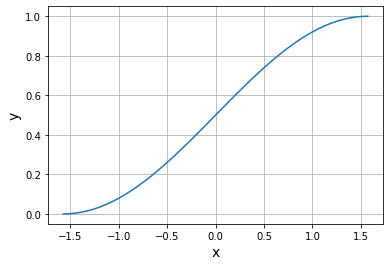
#准备正确数据
#学习sin()曲线,由于只有一个神经元只能学习曲线的一部分所以只使用-pi/2到pi/2之间的曲线,又sigmoid只能输出0-1要将正确的值调整到这个范围内
import numpy as np
import matplotlib.pyplot as plt
X=np.linspace(-np.pi/2,np.pi/2)
T=(np.sin(X)+1)/2#使正确值都在0-1之间
plt.plot(X,T)
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
权重与偏置的更新
推导过程略
w
=
w
?
η
?
E
?
w
=
x
δ
b
=
b
?
η
?
E
?
b
=
δ
δ
=
(
y
?
t
)
(
1
?
y
)
y
(3-3)
w=w-\eta\cfrac{\partial E}{\partial w}=x\delta \\ b=b-\eta\cfrac{\partial E}{\partial b}\tag{3-3}=\delta\\ \delta=(y-t)(1-y)y
w=w?η?w?E?=xδb=b?η?b?E?=δδ=(y?t)(1?y)y(3-3)
列出公式
u
=
x
w
+
b
(3-4)
u=xw+b\tag{3-4}
u=xw+b(3-4)
y
=
f
(
u
)
(3-5)
y=f(u)\tag{3-5}
y=f(u)(3-5)
w
=
w
?
η
?
E
?
w
=
x
δ
(3-6)
w=w-\eta\cfrac{\partial E}{\partial w}=x\delta\tag{3-6}
w=w?η?w?E?=xδ(3-6)
b
=
b
?
η
?
E
?
b
=
δ
(3-7)
b=b-\eta\cfrac{\partial E}{\partial b}=\delta\tag{3-7}
b=b?η?b?E?=δ(3-7)
δ
=
(
y
?
t
)
(
1
?
y
)
y
(3-8)
\delta=(y-t)(1-y)y\tag{3-8}
δ=(y?t)(1?y)y(3-8)
输入与正确数据
import numpy as np
import matplotlib.pyplot as plt
X=np.linspace(-np.pi/2,np.pi/2)#输入
T=(np.sin(X)+1)/2#正确数据
n_data=len(T)
正向传播和反向传播
#正向传播
def forward(x,w,b):
u=x*w+b
y=1/(1+np.exp(-u))
return y
#反向传播,优化参数
def backward(x,y,t):
delta=(y-t)*(1-y)*y
grad_w=x*delta
grad_b=delta
return (grad_w,grad_b)
#结果显示
def show_output(X,Y,T,epoch):
plt.plot(X,T,linestyle="dashed")#虚线画出正确数据
plt.scatter(X,Y,marker="+")#散点图显示输出
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
print("Epoch:",epoch)
print("Error:",1/2*np.sum((Y-T)**2))#误差
#---梯度下降学习---
eta=0.1
epoch =100
#初值
w=0.2
b=-0.2
for i in range(epoch):
if i<10:#仅显示前10期的学习进度
Y=forward(X,w,b)
show_output(X,Y,T,i)
#每一个epoch都使用随机抽取样本进行反向传播训练
idx_rand=np.arange(n_data)#从0开始到n_data-1的整数
np.random.shuffle(idx_rand)#打乱
for j in idx_rand:#随机样本
x=X[j]
t=T[j]
y=forward(X,w,b)
grad_w,grad_b=backward(x,y,t)#反向传播
w-=eta*grad_w
b-=eta*grad_b
Y=forward(X,w,b)#显示最终结果
show_output(X,Y,T,epoch)
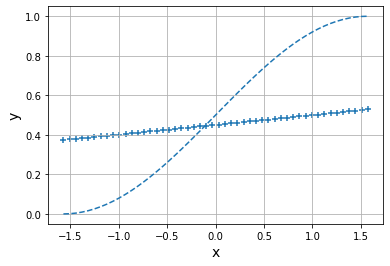
Epoch: 0
Error: 2.4930145826202508
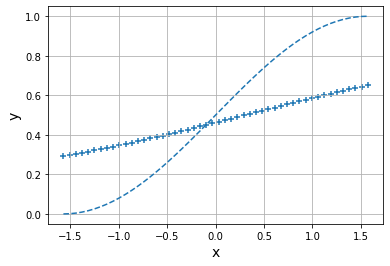
Epoch: 1
Error: 1.577394653470916
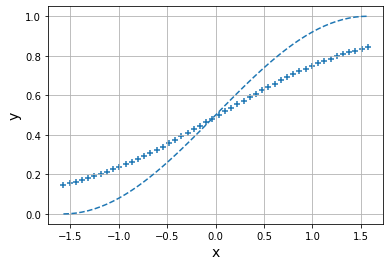
Epoch: 2
Error: 1.0861769315491316
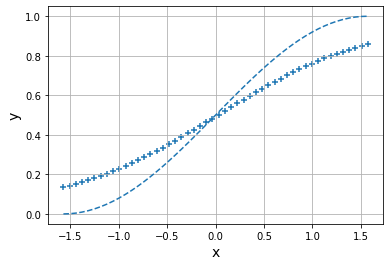
Epoch: 3
Error: 0.8038342421209601
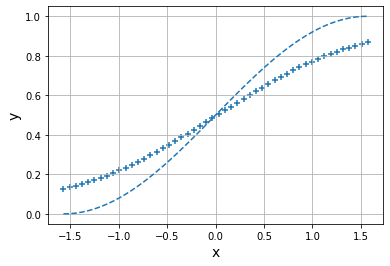
省略剩余的epoch
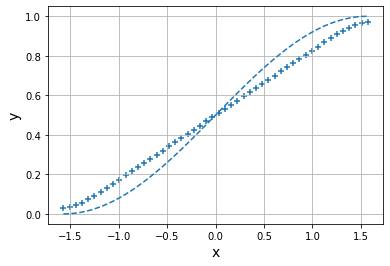
Epoch: 100
Error: 0.11897860684226028
迈向深度学习
多层神经网络的正向传播和反向传播
正向传播:
一个神经元可以有多个输入
u
=
∑
k
=
1
n
w
k
x
k
+
b
y
=
f
(
u
)
u=\sum\limits_{k=1}^nw_kx_k+b\\ y=f(u)
u=k=1∑n?wk?xk?+by=f(u)
反向传播:
δ
=
?
E
?
u
=
?
E
?
y
?
y
?
u
\delta=\cfrac{\partial E}{\partial u}=\cfrac{\partial E}{\partial y}\cfrac{\partial y}{\partial u}
δ=?u?E?=?y?E??u?y?
同单一神经元
?
E
?
w
i
=
x
δ
?
E
?
b
=
δ
\cfrac{\partial E}{\partial w_i}=x\delta\\\cfrac{\partial E}{\partial b}=\delta
?wi??E?=xδ?b?E?=δ
对于
?
y
?
u
\cfrac{\partial y}{\partial u}
?u?y?可以使用该层的激活函数求得
而对中间层求
?
E
?
y
\cfrac{\partial E}{\partial y}
?y?E?因为这一层的y是下一层的输入所以需要知道下一层(接近输出的层)的信息
?
E
?
y
=
∑
j
=
1
m
?
E
?
u
j
(
n
l
)
?
u
j
(
n
l
)
?
y
\cfrac{\partial E}{\partial y}=\sum\limits_{j=1}^m\cfrac{\partial E}{\partial u_j^{(nl)}}\cfrac{\partial u_j^{(nl)}}{\partial y}
?y?E?=j=1∑m??uj(nl)??E??y?uj(nl)??
n
l
nl
nl代表是该层下一层的变量,本质上还是链式求导法则E为输出层的误差由变量
u
(
n
l
)
u^{(nl)}
u(nl)组成而
u
(
n
l
)
u^{(nl)}
u(nl)又由上一层的输出y作为
u
(
n
l
)
u^{(nl)}
u(nl)的输入变量所以可以通过链式求导得出中间层的偏微分。
上面的
?
E
?
u
j
(
n
l
)
\cfrac{\partial E}{\partial u_j^{(nl)}}
?uj(nl)??E?可以由
δ
\delta
δ表示
δ
j
n
l
=
?
E
?
u
j
(
n
l
)
\delta^{nl}_j=\cfrac{\partial E}{\partial u_j^{(nl)}}
δjnl?=?uj(nl)??E?
又
?
u
j
(
n
l
)
?
y
=
w
j
n
l
?
w
j
(
n
l
)
\cfrac{\partial u^{(nl)}_j}{\partial y}=w_j^{nl}\ w^{(nl)}_j
?y?uj(nl)??=wjnl??wj(nl)?是y作为下一层输入对y叠加的权重,所以:
?
E
?
y
=
∑
j
=
1
m
δ
j
(
n
l
)
w
j
(
n
l
)
\cfrac{\partial E}{\partial y}=\sum\limits_{j=1}^m\delta_j^{(nl)}w_j^{(nl)}
?y?E?=j=1∑m?δj(nl)?wj(nl)?
通过这种方式依次从输出层到各级中间层最后到输入层更新参数,这种反向传播算法也称为误差反向传播法,此外可以通过矩阵同时对层内所有神经元进行处理。