开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 机器学习常考问题面经总结 -> 正文阅读

[人工智能]机器学习常考问题面经总结

1 特征工程

对于一个机器学习问题，数据和特征往往决定了结果的上限，而模型、算法的选择应优化则是在逐步接近这个上限。

1.1 特征归一化

为了消除数据特征之间的量纲影响，我们需要对特征进行归一化处理使得不同指标之间具有可比性。

1 归一化方法

最小最大法（Min-Max Scaling）： $\frac{X-X_{min}}{X_{max}-X_{max}}$
0均值归一化（Z-score Normalization）： $=\frac{x-u}{\sigma}$

2 为什么需要归一化

前面说的为了去量纲，进一步，为什么需要去量纲？拿一个随机梯度下降的例子，假设高两种数值型特征， X1 的取值范围为[0, 10],X2的取值范围为[0, 3］，于是可以构造一个目标函数等值图。另外进行归一化之后如右图
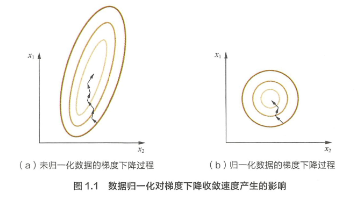
在这里插入图片描述
可以看出，如果进行归一化后，等值图是一个圆，可以更快的找到最优点。所以一般通过梯度下降求解的就是需要归一化的。比如线性回归，逻辑回归，SVM，NN。但对于决策树没必要，因为决策树在进行节点分裂时，主要通过计算特征x的信息增益/比/Gini系数。涉及到信息熵与归一化与否都没关系。

1.2 类别型特征

类比特征就是待分类的标签值。比如男女，血型A/B/O/AB.这些字符串表示出了决策树等少数模型可以接受，一般模型比如LR,SVM都需要数值型标签才能work。

序号编码：比如考试分数等级（ABC）可以表示为3，2，1，依旧保留了类别的大小关系
独热编码（one-hot）：通常用于处理类别不具有大小关系的类别。比如（A/B/O/AB）血型。
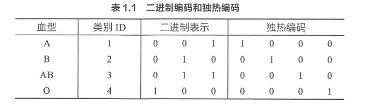
二进制编码：首先给类别进行编号，得到ID，然后以二进制作为其编码表示。二进制编码本质上是利用二进制对 ID 进行哈希映射，最终得到 0/1 特征向量，且维数少于独热编码，节省了存储空间。

1.3 组合特征

为了提高对复杂关系的拟合能力，需要对一特征进行组合交叉，将一阶特征组合为高阶特征。

1.4 文本表示能力

1 Word2Vec

2013年谷歌提出了Word2Vec模型。有两种网络结构分别是：

Cbow
Skip-gram

CBOW 和 Skip-gram 都可以表示威由输入层映射层和输出层组成的神经网络。
输入层中的每个词由独热编码方式表示，即所有词均表示为N维向量，N 为词汇表中单词的总数。在向量中，每个词都将与之对应的维度为1，其余维度的值均设为 0 。在映射层（又称隐含层）中， K 个隐含单元（ Hidden Units ）的取值可以由 N 维输入向量以及连接输入和隐含单元之间的 N×K 维权重矩阵计算得到。在 CBOW 中，还需要将各个输入词所计算出的隐含单元求和。

同理，输出层向量的值可以通过隐含层向量（ K 维），以及连接隐含层和输出层之间的 K× N 维权童声巨阵计算得到。输出层也是一个N维向量，每维与词汇表中的一个单词中日对应。最后，对输出层向量应用Softmax 激活函数，可以计算出每个单词的生成概率。
在这里插入图片描述

2 Word2Vec和LDA区别联系

首先， LDA 是利用文档中单词的共现关系来对单词按主题聚类，也可以理解为对“文档-单词”矩阵进行分解得到“文档-主题”和“主题-单词”两个概率分布。而 Word2Vec 真实是对“ 上下文－单词”矩阵进行学习。
主题模型和词嵌入两类方法最大的不同在于模型本身，主题模型是一种基于概率圄模型的生成式模型，似然函数可以写成若干条件概率连乘的形式，其中包括需要推测的隐含变量（即主题）；而词嵌入模型一般表达为神经网络的形式，似然函数定义在网络的输出之上，需要通过学习网络的权重以得到单词的稠密向量表示。

2 模型评估

2.1 评估指标

指标	T（预测正类）	F（预测负类）
Positive(正类)	TP	FP
Negative(负类)	TN	FN

$准确率： A c c u r a c y = T F + F N / T F + T N + F P + F N$
Acc缺陷：对于正负样本不均衡的条件下，比如负样本99%，即使所有样本分类为-1，也是99%的准确率。
$精确率： P r e c i s i o n = T P / T P + F P$
P指标又称为查准率，正类分类正确占比所有分类为正的比例。
$召回率： R e c a l l = T P / T P + F N$
R指标又称为查全率，正类分类为正占比真正正类的比例。
$F 1 s c o r e = 2 P R / (P + R)$
PR是一对矛盾的指标，为了均衡P和R指标，综合评价模型。

P-R曲线
P-R曲线越靠近右上角效果越好，通过移动判定阈值来绘制曲线。也是为了综合的评价模型。
在这里插入图片描述

2.2 ROC和AUC

1 ROC曲线

ROC的横坐标是假阳（FPR），纵坐标是真阳（TPR），计算方式如下：

指标	T（预测正类）	F（预测负类）
Positive(正类)	2	1
Negative(负类)	1	6
FPR	1/1+2=2/3
TPR	1/1+6=1/7

绘制ROC曲线：
对于以下的分类结果：
在这里插入图片描述
按照输出概率从大到小，作为阈值，每个阈值对应一组FPR，TPR，得到ROC曲线：

还有一种方法：
统计正负样本的个数P，N。设置横轴的刻度为1/N，纵轴的1/P。对结果按照输出概率降序排序，依次遍历样本，遇到一个正样本就沿y轴前进一个刻度，反之x轴。遍历完所有样本即达到（1，1）点。

2 AUC的计算

AUC就是ROC的曲线面积，可以使用对曲线积分的方式计算。
一般AUC取值（0.5，1）,越大越好，说明分类器将正样本排序在前，这就是AUC的物理意义。

3 ROC和P-R曲线对比

ROC比P-R曲线更加稳定，对于正负样本不均衡时，ROC曲线可以维持不变，但是P-R曲线变化剧烈。所以ROC的应用场景更加广泛。
在这里插入图片描述

2.3 余弦相似度

1 余弦相似度和欧氏距离

对于词频或者词向量，他们在空间的欧氏距离可能很大，但是余弦夹角很小，依次度量两个向量的相似度。即是扩展到高维数据，依然符合相似为1，相交为0，相反为-1的特点。所以余弦相似度取值为[0，2]。

在一些场景，例如 Word2Vec 中，其向量的模长是经过归一化的，此时欧氏距离与余弦距离有着单调的关系, 即
$\|A-B\|_{2}=\sqrt{2(1-\cos (A, B))},$
其中 $A-B\|_{2}$ 表示欧氏距离, $\cos (A, B)$ 表示余弦相似度, $(1-\cos (A, B))$ 表示余弦距离。在此场景下, 如果选择距离最小 (相似度最大) 的近邻, 那么使用余弦相似度和欧氏距离的结果是相同的。

总体来说，欧氏距离体现数值上的绝对差异，而余弦距离体现方向上的相对差异。例如, 统计两部剧的用户观看行为, 用户 $\mathrm{A}$ 的观看向量为 $(0, 1)$ , 用户 $\mathrm{B}$ 为 $(1, 0)$ ; 此时二者的余弦距离很大, 而欧氏距离很小; 我们分析两个用户对于不同视频的偏好, 更关注相对差异, 显然应当使用余弦距离。而当我们分析用户活跃度，以登陆次数 (单位: 次) 和平均观看时长 (单位: 分钟) 作为特征时, 余弦距离会认为 $(1, 10) 、 (10, 100)$ 两个用户距离很近; 但显然这两个用户活跃度是有着极大差异的, 此时我们更关注数值绝对差异，应当使用欧氏距离。

所以，针对不同的场景采用不同的距离度量方式。

2 余弦距离不是一个严格定义的距离

距离定义：在集合中，一对元素均可以唯一确定一个实数，满足正定性，对称性和三角不等式，那么这个实数就是这对元素的距离。但是余弦距离不满足三角不等式。

此外还有KL散度（相对熵）不满足对称性和三角形不等式

2.5 A/Btest

1.为什么进行A/Btest？

离线评估无法完全消除模型过拟合想象，无法代替线上实验结果
离线条件距离线上的环境有一定区别，比如延迟，数据丢失等等
线上的商业指标在线下无法计算，比如点击率，留存时长，pv访问量等等，这些都需要A/B test来获取。

2.如何进行A/B test？

对用户进行分桶，实验组和对照组。要注意样本的独立性和采样无偏性，确保同一用户每次分进同一个组。分桶过程中用户id是一个随机数，保证无偏。

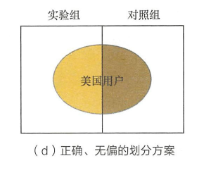
3.如何划分实验组和对照组？

对于美国用户进行推荐系统a/btest，按照用户id的奇偶性来划分两组，分别采用不同的模型。
在这里插入图片描述

2.6 模型评估方法

1 holdout法

7:3的训练测试比例

缺点：，即在验证集上计算出来的最后评估指标与原始分组有很大关系。为了消除随机性，研究者们引入了“交叉检验”的思想

2 交叉检验

k-fold交叉验证：将数据样本等分为k份，依次选择其中一份为测试集，其他为训练集，作k次实验，k次结果平均为最终的评估指标。

留一：每次留下一个样本作为测试集，进行n次实验，取平均，由于遍历时间过长，工程上不采用。

3 自助采样法（booststrap）

以上方法都有一个缺点：当样本规模比较小时，将样本集进行划分会让训练集进一步减小，这可能会影响模型训练效果。自助法可以维持数据集的规模。

对于总数为 n 的样本集合进行 n 次有放回的随机抽样得到大小为 n 的训练集。 n 次采样过程中有的样本会被重复采样，有的样本没高被抽出过，将这些没被抽出的样本作为测试集，进行模型验证，这就是自助法的验证过程。

4 自助法下，n次取样多少样本未被抽中? 36.8%

在这里插入图片描述

2.7 过拟合与欠拟合问题

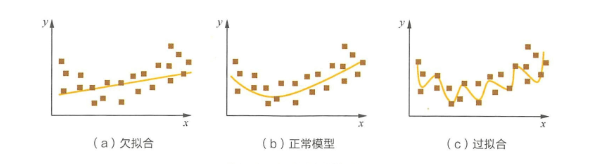
在这里插入图片描述

1 如何降低过拟合？

数据层：更多的训练数据，使得模型学习到更多有效的特征，减小噪声影响。
模型层面：降低模型复杂度。神经网络中减少神经层数，神经元个数；决策树中减少树的深度，剪枝等。
正则化：使用L1或者L2正则。给模型的参数加约束，避免权重值过大带来的过拟合风险。
集成学习方法，比如Boosting，Bagging，Stacking。

2 欠拟合怎么操作？

增加新特征：但特征不足或者表现不好时就会出现欠拟合现象，通过增加新的特征，或者使用特征交叉方法等等，比如FM，GBDT，Deep Crossing等深度学习方法。
增加模型复杂度：神经网络中增加层数和单元数，线性模型增加高次项等等。
减小正则化系数

2.8 方差和偏差

关于方差和偏差的总结方差和偏差

3 分类算法

3.1 逻辑回归

1 逻辑回归与线性回归的比较

不同之处：

LR是分类，线性回归属于回归

相同：

线性回归使用最小二乘，实际就是极大似然估计的一个化简，LR使用对数似然函数作为损失函数。
都可以使用SGD进行求解

2 LR如何进行多分类

1.当单个样本属于一个标签时
假设每个样本属于不同标签的概率服从几何分布，
$h_{\theta}(x)=\left[\begin{array}{c} p(y=1 \mid x ; \theta) \\ p(y=2 \mid x ; \theta) \\ \vdots \\ p(y=k \mid x ; \theta) \end{array}\right]=\frac{1}{\sum_{j=1}^{k} \mathrm{e}^{\theta_{j}^{\top} x}}\left[\begin{array}{c} \mathrm{e}^{\theta_{1}^{\top} x} \\ \mathrm{e}^{\theta_{2}^{\top} x} \\ \vdots \\ \mathrm{e}^{\theta_{k}^{\top} x} \end{array}\right]$
其中 $\theta_{1}, \theta_{2}, \ldots, \theta_{k} \in \mathbb{R}^{n}$ 为模型的参数，而 $\frac{1}{\sum_{j=1}^{k} \mathrm{e}^{\theta_{i}^{T} x}}$ 可以看作是对概率的归一化。为了方便起见, 我们将 $\left\{\theta_{1}, \theta_{2}, \ldots, \theta_{k}\right\}$ 这 $k$ 个列向量按顺序排列形成 $\times k$ 维矩阵, 写作 $\theta$ , 表示整个參数集。一般来说, 多项逻辑回归具有参数冗余的特点, 即将 $\theta_{1}, \theta_{2}, \ldots, \theta_{k}$ 同时加减一个向量后预测结果不变。特别地, 当类别数为 2 时,
$h_{\theta}(x)=\frac{1}{\mathrm{e}^{\theta_{1}^{\top} x}+\mathrm{e}^{\theta_{2}^{\top} x}}\left[\begin{array}{c} \mathrm{e}^{\theta_{1}^{\mathrm{x}} x} \\ \mathrm{e}^{\theta_{2}^{\mathrm{T}} x} \end{array}\right]$
利用参数只余的特点，我们将所有参数减去 $\theta_{1}$ , 变为：
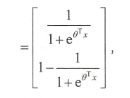
在这里插入图片描述

其中 $\theta=\theta_{2}-\theta_{1}$ 。而整理后的式子与逻辑回归一致。因此，多项逻辑回归实际上是二分类逻辑回归在多标签分类下的一种拓展。

2.当一个样本可能属于多标签时：
我们可以训练 k 个二分类的逻辑回归分类器。第i个分类器区分每个样本是否可以归为第 i 类，训练该分类器时需要把标签重新整理为“第 i 类标签 ” 与"其他标签”两类。

3 LR的优缺点

优点

处理速度快，容易并行计算，是用于学习大规模训练的样本和特征

缺点：

需要大量的特征组合和离散来增强特征的表达性
模型表达能力弱
容易欠拟合

4 LR为何使用sigmoid激活函数（sigmoid函数的优点）

$\frac{e^x}{1+e^x}$

函数单调递增，属于（0，1）范围内，所以可以作为分类的阈值函数。
函数关于（0,0.5）对称
其导数是自身的函数，计算导数很简单 $p^{'} = p (1 ? p)$

3.2 支持向量机

3.3 决策树

决策树

1 决策树有哪些常用的启发函数

1.ID3——最大信息增益
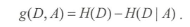
在这里插入图片描述
2.C4.5——最大信息增益比

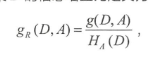
3.CART——最大基尼指数（Gini）
基尼指数描述的是数据得纯度，类似信息熵的含义。

CART 在每一次迭代中 选择基尼指数最小（ID3，C4.5选择最大的）的特征及其对应的切分点进行分类。但与 ID3 , C4.5 不同的是， CART 是一颗二叉树，采用二元切割，每一步将数据按特征 A 的取值切成两份，分别进入左右子树
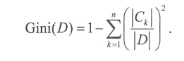
在这里插入图片描述
总结：

信息增益反映的是给定条件以后不确定性减少的程度，特征对应的取值越多就意昧着确定性更高，也就是条件熵越小，信息增益越大。这在实际应用中是个缺陷。比如引入特征DNA，每个人的DNA都不一样，所以ID3按照DNA特征进行划分一走是最优的（条件熵=0 ），但这种分类的泛化能力是非常弱的。因此， C4.5 实际上是对 ID3 进行优化 3 通过引入信息增益比一定程度上对取值比较多的特征进行惩罚，避免 ID3 出现过拟台的特性，C4.5提升决策树的泛化能力。
从样本角度，ID3只能处理离散型变量，后两者可以处理离散+连续。
- C4.5： 通过对数据排序之后找到类别不同的分割线作为切分点，根据切分点把连续属性转为布尔型，从而将连续型变量转操多个取值区间的离散型变量。
- CART：由于构建时每次都会对特征进行二值划分，因此可以很好地适用于连续性变量。

2 决策树怎么剪枝

一颗完全生长的决策树都会过拟合，预测效果很差，为了提升决策树的泛化能力，需要对决策树进行剪枝，去除一些特征。主要有两种方法，预剪枝（pre-Pruning）和后剪枝（Post-Pruning）。

预剪枝：在树中结点进行扩展之前，先计算当前的划分是否能带来模型泛化能力的提升，如果不能，则不再继续生长子树。此时可能存在不同类别的样本同时存在结点中，按照多数投票的原则判断该结点所属类别。预剪枝对于何时停止决策树的生长有以下几种方法：
1. 树深度达到一定深度，停止
2. 当前节点的样本少于某一个阈值，停止生长
3. 计算每次分裂对于测试集的准确度提升，小于阈值停止生长
后剪枝：先生长出一颗完全的树，再从下向上进行剪枝，删除子树，用一个叶子结点代替，该节点的类别同样按照多数投票的原则进行判断。同样地后剪枝也可以通过在测试集上的准确率进行判断，如果剪枝过后准确率有所提升，则进行剪枝。

总结：