[人工智能]MIND模型

Multi-Interest Network with Dynamic Routing for Recommendation at Tmall

1.胶囊网络

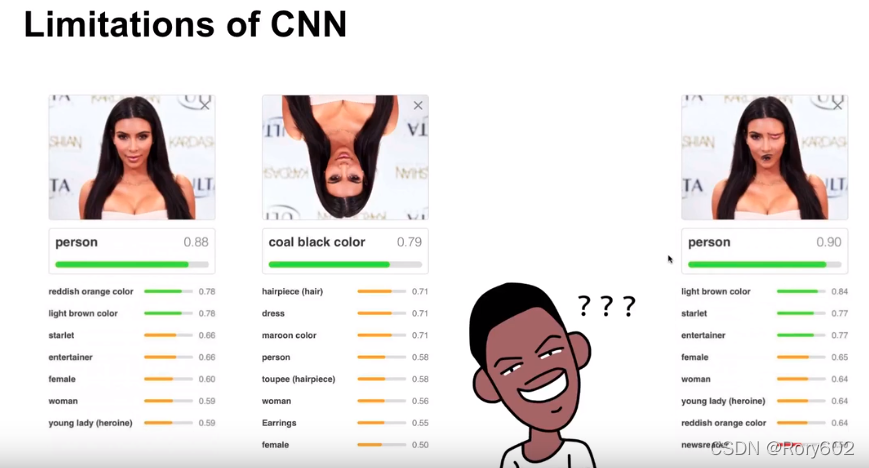
将图像倒立，识别率会下降，将眼睛和嘴调换位置，仍能识别为人，所以CNN缺乏对相对空间位置的表达。

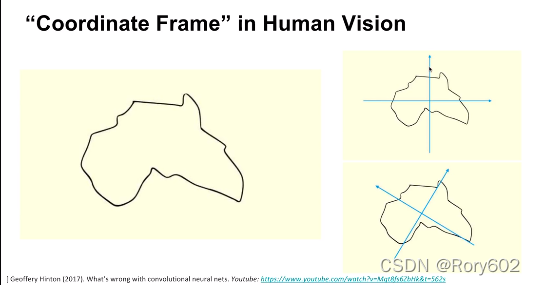
非洲还是澳大利亚？转换坐标系，其实是非洲。

low level capsule转化为high level capsule, 每个low level相当于表示实体的不同部分， high level表示整个实体。

三角形的第1个分量表示方向，整个 范数表示实体存在的置信度。

1.1胶囊网络和传统的神经网络的区别

传统的神经网络：（1）标量输入到标量输出的过程。（2）累积求和->激活函数输出

胶囊神经网络：（1）向量输入到向量输出的过程。（3）放射变换(向量乘以矩阵转化为另一个 向量)->通过c做线性加权求和->挤压（squash）->输出v。其中c是通过dynamic routing机制动态决定的。

$\frac{\Vert s{\Vert }^2}{1+\Vert s{\Vert }^2}$： squash类似sigmoid变换的函数，当s的 向量特别长，接近无穷时，将它压缩为1，当s为0时为0.

$\frac{s}{\Vert s\Vert }$为标准化的过程。

$b_{11}和b_{21}$初始化0，b可以理解为agreement（选举的意思，类似总统选举），其中$u_1和u_2$类似总统候选人。b经过softmax生成和为1的权重。经过squash会生成$a_1$, $a_1$和$u_1$的夹角比较接近，就b（agreement）就会靠近$u_1$，update agreement。类似kmeans中心点的计算。v的范数表示confidence。范数很大，表示概率很大。

训练过程： 如果是minist数据集，假设训练的正样本为1，我门希望为的1范数会比较大，其他的范数比较小。

2. MIND

2.1问题的公式表示

匹配阶段的主要目标就是对每个用户$u\in \mathcal{U}$在几十亿item池子中$\mathcal{I}$，候选集的数量大约几千左右。

每个样本可以用$\left({\mathcal{I}}_u,{\mathcal{P}}_u,{\mathcal{F}}_i\right)$表示，其中${\mathcal{I}}_u$表示与用户交互的item（或者说用户的行为）。${\mathcal{P}}_u$表示用户的基本信息（例如：用户的性别、年龄）。${\mathcal{F}}_i$表示目标 item（例如：item id和category id）。

将原始特征映射为用户表示：
$${\mathrm{V}}_u=f_{\text{user?}}\left(I_u,{\mathcal{P}}_u\right)\text{\hspace{1em}(1)}$$

其中：${\mathrm{V}}_u=\left({\mathbf{v}}_u^1,\dots ,{\mathbf{v}}_u^K\right)\in {\mathbb{R}}^{d\times K}$用来表示用户$u$的向量，$d$表示向量维度，$K$表示用户表示的数量，$K=1$表示只有一个向量被使用 ，就像YouTube DNN。

target item $i$的向量表示为：
$${\mathbf{e}}_i=f_{\text{item?}}\left({\mathcal{F}}_i\right)\text{\hspace{1em}(2)}$$
其中：$e_i\in {\mathbb{R}}^{d\times 1}$表示item $i$ 的一个向量。

Top N候选集计算：
$$f_{\text{score?}}\left({\mathrm{V}}_u,{\mathbf{e}}_i\right)=\underset{1\le k\le K}{\max }{\mathbf{e}}_i^{\mathrm{T}}{\mathbf{v}}_u^k\text{\hspace{1em}(3)}$$
$N$表示候选集的数量。

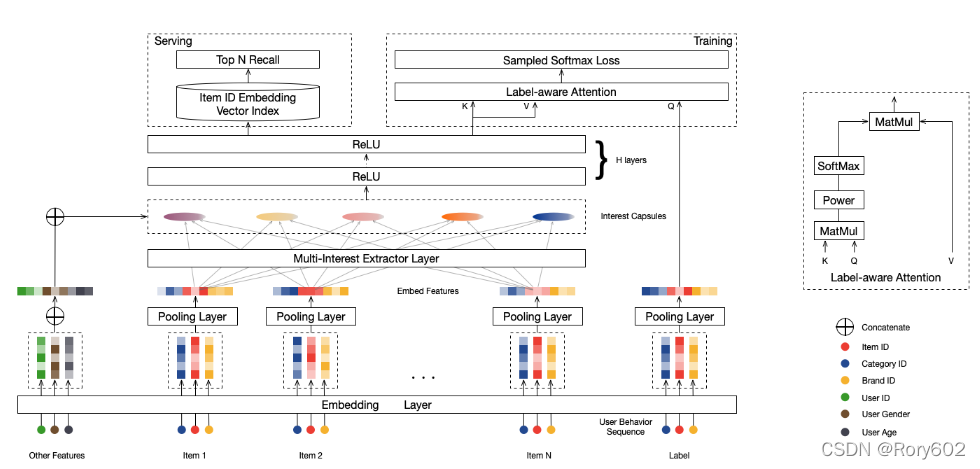
2.2嵌入和池化层

MIND的 输入特征包括3部分：用户属性特征${\mathcal{P}}_u$、用户的行为特征${\mathcal{I}}_u$和标签item${\mathcal{F}}_i$
${\mathcal{P}}_u$(性别、年龄)进行concatenate。

${\mathcal{F}}_i$（品牌id, shop id）传入average pooling 层，形成item embedding 为$e_i$。

${\mathcal{I}}_u$用户的行为序列，${\mathrm{E}}_u=\left\{{\mathbf{e}}_j,j\in I_u\right\}$。

2.3 多兴趣提取层

对用户的历史行为进行聚类

2.3.1 动态路由

假设有两个capsules, low-level capsules c ? i l ∈ R N l × 1 , i ∈ { 1 , … , m } \vec{c}_{i}^{l} \in \mathbb{R}^{N_{l} \times 1}, i \in\{1, \ldots, m\} c il?∈RNl?×1,i∈{1,…,m} 和high-level capsules c ? j h ∈ R N h × 1 , j ∈ { 1 , … , n } \vec{c}_{j}^{h} \in \mathbb{R}^{N_{h} \times 1}, j \in \{1, \ldots, n\} c jh?∈RNh?×1,j∈{1,…,n}

low-level capsule $i$和 high-level capsule $j$之间的logit $b_{ij}$计算公式如下：
$$b_{ij}={\left(c_j^h\right)}^T{\mathrm{S}}_{ij}{c}_i^l\text{\hspace{1em}(4)}$$
其中，${\mathrm{S}}_{ij}\in {\mathbb{R}}^{N_h\times N_l}$是需要学习的双线性映射矩阵。

candidate vector for high-level capsule j
$$z_j^h=\sum _{i=1}^m{w}_{ij}{\mathrm{S}}_{ij}{\mathbf{c}}_i^l\text{\hspace{1em}(5)}$$
$w_{ij}$是连接low-level和high-level之间的权重，计算方式如下：
$$w_{ij}=\frac{\exp b_{ij}}{{\sum }_{k=1}^m\exp b_{ik}}\text{\hspace{1em}(6)}$$
quash 函数应用于high-level capsules， 计算方式如下：
$$c_j^h=\mathrm{squash}\left(z_j^h\right)=\frac{{\Vert z_j^h\Vert }^2}{1+{\Vert \mid z_j^h\Vert }^2}\frac{z_j^h}{\Vert z_j^h\Vert }\text{\hspace{1em}(7)}$$
$b_{ij}$初始化为0， 当路由结束，$c_j^h$可以固定下来，作为下一层的输入。

使用Shared bilinear mapping matrix主要考虑两点：从低阶的用户行为胶囊中学习高阶的用户兴趣胶囊（1）用户行为是变长的，我们希望模型更加通用。（2）我们希望用户行为和用户兴趣能够在一个向量空间中。
b i j = u ? j T ? S e → i , i ∈ I u , j ∈ { 1 , … , K } (8) b_{i j}=\vec{u}_{j}^{T} \mathrm{~S} \overrightarrow{\boldsymbol{e}}_{i}, \quad i \in I_{u}, j \in\{1, \ldots, K\}\tag{8} bij?=u jT??Se i?,i∈Iu?,j∈{1,…,K}(8)
$e_i\in {\mathbb{R}}^d$表示item $i$的用户行为，$u_j\in {\mathbb{R}}^d$表示用户兴趣胶囊$j$。$S\in {\mathbb{R}}^{d\times d}$是用户行为胶囊和用户兴趣胶囊之间的共享矩阵。

**初始化routing logits：**如果矩阵初始化为0，会导致用户兴趣相同，因此采用高斯分布进行初始化。

动态用户兴趣的数量：
$$K_u^{\prime }=\max \left(1,\min \left(K,{\log }_2\left(\left|I_u\right|\right)\right)\right)\text{\hspace{1em}(9)}$$
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7vklCkM8-1642259038786)(Selection_006.png)]

def build(self, input_shape):
    self.routing_logits = self.add_weight(shape=[1, self.k_max, self.max_len],
                                          initializer=RandomNormal(stddev=self.init_std),
                                          trainable=False, name="B", dtype=tf.float32)
    self.bilinear_mapping_matrix = self.add_weight(shape=[self.input_units, self.out_units],
                                                   initializer=RandomNormal(stddev=self.init_std),
                                                   name="S", dtype=tf.float32)
    super(CapsuleLayer, self).build(input_shape)

def call(self, inputs, **kwargs):
    behavior_embddings, seq_len = inputs
    batch_size = tf.shape(behavior_embddings)[0]
    seq_len_tile = tf.tile(seq_len, [1, self.k_max])

    for i in range(self.iteration_times):
        mask = tf.sequence_mask(seq_len_tile, self.max_len)
        pad = tf.ones_like(mask, dtype=tf.float32) * (-2 ** 32 + 1)
        routing_logits_with_padding = tf.where(mask, tf.tile(self.routing_logits, [batch_size, 1, 1]), pad)
        weight = tf.nn.softmax(routing_logits_with_padding)
        behavior_embdding_mapping = tf.tensordot(behavior_embddings, self.bilinear_mapping_matrix, axes=1)
        Z = tf.matmul(weight, behavior_embdding_mapping)
        interest_capsules = squash(Z)
        delta_routing_logits = reduce_sum(
            tf.matmul(interest_capsules, tf.transpose(behavior_embdding_mapping, perm=[0, 2, 1])),
            axis=0, keep_dims=True
        )
        self.routing_logits.assign_add(delta_routing_logits)
    interest_capsules = tf.reshape(interest_capsules, [-1, self.k_max, self.out_units])
    return interest_capsules

2.3.2 Label-aware Attention

根据 用户的兴趣胶囊和item向量进行attention计算，对item进行加权。label是query, 兴趣胶囊是keys和values。user u的输出向量和item i计算方式如下：
$$\begin{array}{rl}{v}_u& =\text{?Attention?}\left(e_i,{\mathrm{V}}_u,{\mathrm{V}}_u\right)\\ & ={\mathrm{V}}_u\mathrm{softmax}\left(\mathrm{pow}\left({\mathrm{V}}_u^{\mathrm{T}}{e}_i,p\right)\right)\end{array}$$
其中, $p$是调整attention分布的参数，当p为0时， attention是平均的。$p$越大，趋近于无穷时，value更加关注权重最大的值，忽略其他的项。

def call(self, inputs, training=None, **kwargs):
    keys = inputs[0]
    query = inputs[1]
    weight = reduce_sum(keys * query, axis=-1, keep_dims=True)
    weight = tf.pow(weight, self.pow_p)  # [x,k_max,1]

    if len(inputs) == 3:
        k_user = tf.cast(tf.maximum(
            1.,
            tf.minimum(
                tf.cast(self.k_max, dtype="float32"),  # k_max
                tf.log1p(tf.cast(inputs[2], dtype="float32")) / tf.log(2.)  # hist_len
            )
        ), dtype="int64")
        seq_mask = tf.transpose(tf.sequence_mask(k_user, self.k_max), [0, 2, 1])
        padding = tf.ones_like(seq_mask, dtype=tf.float32) * (-2 ** 32 + 1)  # [x,k_max,1]
        weight = tf.where(seq_mask, weight, padding)

    weight = softmax(weight, dim=1, name="weight")
    output = reduce_sum(keys * weight, axis=1)

    return output

2.3.3 Training&Serving

得到用户的向量$v_u$和标签的向量$e_i$， 计算用户和标签的之间的交互的概率
$$\mathrm{Pr}(i\mid u)=\mathrm{Pr}\left(e_i\mid v_u\right)=\frac{\exp \left(v_u^{\mathrm{T}}{e}_i\right)}{{\sum }_{j\in I}\exp \left(v_u^{\mathrm{T}}{e}_j\right)}\text{\hspace{1em}(10)}$$
训练的目标函数：
$$L=\sum _{(u,i)\in \mathcal{D}}\log \mathrm{Pr}(i\mid u)\text{\hspace{1em}(11)}$$
其中$\mathcal{D}$是包括用户和item的训练数据