机器学习日记（7）
机器学习系统的开发与性能改进
假如你在开发一个机器学习系统，或者想试着改进一个机器学习系统的性能，你应如何决定接下来应该选择哪条道路？为了解决这一问题，我想仍然使用预测房价的学习例子，假如你已经完成了正则化线性回归，也就是最小
化代价函数𝐽的值，在你得到你的学习参数以后，你将你的假设函数放到一组新的房屋样本上进行测试，你发现在预测房价时产生了巨大的误差，现在你的问题是要想改进这个算法，接下来应该怎么办？
实际上你可以想出很多种方法来改进这个算法的性能，其中一种普遍的办法是使用更多的训练样本。获得更多的训练实例——通常是有效的，但代价较大，下面的方法也可能有效，可考虑先采用下面的几种方法：
1.尝试减少特征的数量
2.尝试获得更多的特征
3.尝试增加多项式特征
4.尝试减少正则化程度𝜆
5.尝试增加正则化程度𝜆
评估一个假设（Evaluating a Hypothesis）
当我们确定学习算法的参数的时候，我们考虑的是选择参量来使训练误差最小化，有人认为得到一个非常小的训练误差一定是一件好事，但我们已经知道，仅仅是因为这个假设具有很小的训练误差，并不能说明它就一定是一个好的假设函数。而且我们也学习了过拟合假设函数的例子，所以这推广到新的训练集上是不适用的。
那么，你该如何判断一个假设函数是过拟合的呢？对于这个简单的例子，我们可以对假设函数?(𝑥)进行画图，然后观察图形趋势，但对于特征变量不止一个的这种一般情况，还有像有很多特征变量的问题，想要通过画出假设函数来进行观察，就会变得很难甚至是不可能实现。
因此，我们需要另一种方法来评估我们的假设函数过拟合检验。为了检验算法是否过拟合，我们将数据分成训练集和测试集，通常用70%的数据作为
训练集，用剩下30%的数据作为测试集。很重要的一点是训练集和测试集均要含有各种类型的数据，通常我们要对数据进行“洗牌”，然后再分成训练集和测试集。
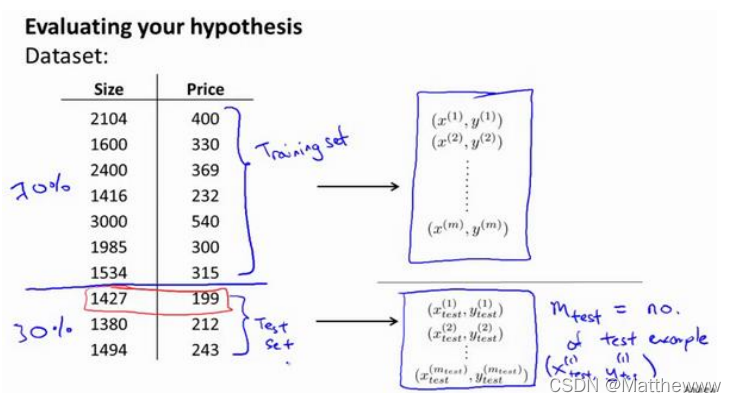
测试集评估在通过训练集让我们的模型学习得出其参数后，对测试集运用该模型，我们有两种方式计算误差：
1.对于线性回归模型，我们利用测试集数据计算代价函数𝐽
2.对于逻辑回归模型，我们除了可以利用测试数据集来计算代价函数外：
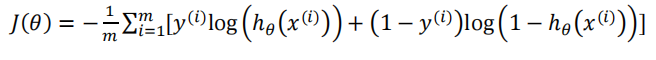
误分类的比率，对于每一个测试集实例，计算：
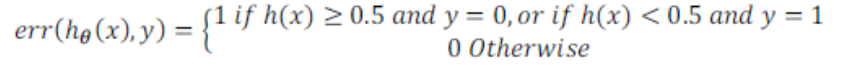
然后对计算结果求平均。
模型选择和交叉验证集（Model Selection and Train_Validation_Test Sets）
假设我们要在 10 个不同次数的二项式模型之间进行选择：
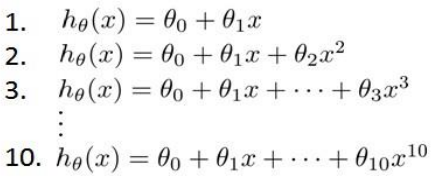
显然越高次数的多项式模型越能够适应我们的训练数据集，但是适应训练数据集并不代表着能推广至一般情况，我们应该选择一个更能适应一般情况的模型。我们需要使用交叉验证集来帮助选择模型。
即：使用 60%的数据作为训练集，使用 20%的数据作为交叉验证集，使用 20%的数据作为测试集。
模型选择的方法为：
- 使用训练集训练出 10 个模型
- 用 10 个模型分别对交叉验证集计算得出交叉验证误差（代价函数的值）
- 选取代价函数值最小的模型
- 用步骤 3 中选出的模型对测试集计算得出推广误差（代价函数的值）
线性回归各集代价函数：
诊断偏差和方差（Diagnosing Bias vs. Variance）
当你运行一个学习算法时，如果这个算法的表现不理想，那么多半是出现两种情况：要么是偏差比较大，要么是方差比较大。换句话说，出现的情况要么是欠拟合，要么是过拟合问题。那么这两种情况，哪个和偏差有关，哪个和方差有关，或者是不是和两个都有关？搞清楚这一点非常重要，因为这能判断出现的情况是这两种情况中的哪一种。其实是一个很有效的指示器，指引着可以改进算法的最有效的方法和途径。高偏差和高方差的问题基本上来说是欠拟合和过拟合的问题。
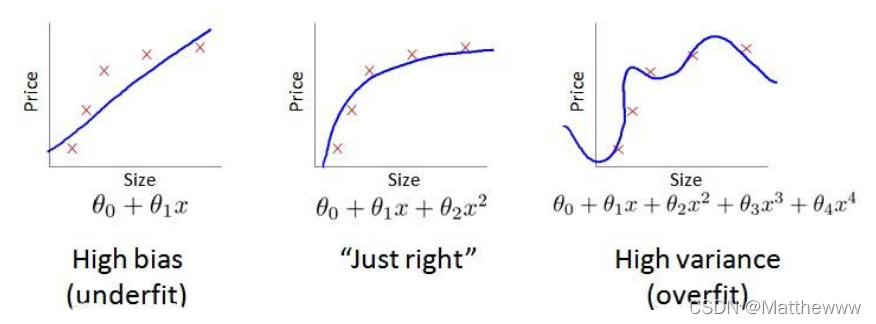
我们通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析：
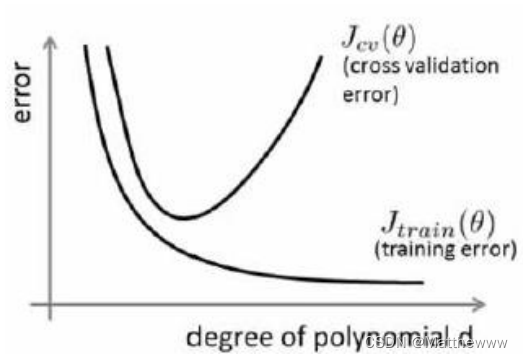
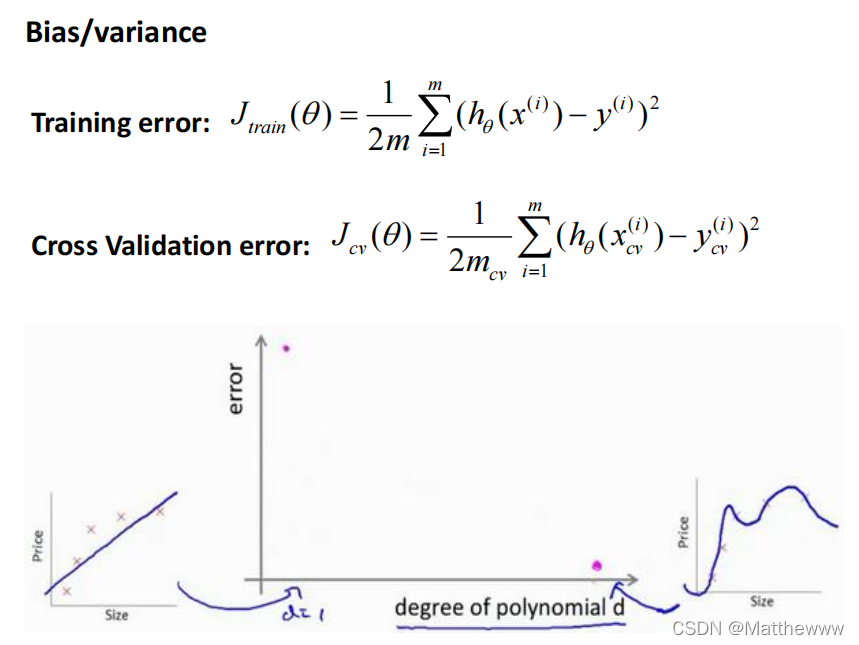
对于训练集，当 𝑑 较小时，模型拟合程度更低，误差较大；随着 𝑑 的增长，拟合程度提高，误差减小。
对于交叉验证集，当 𝑑 较小时，模型拟合程度低，误差较大；但是随着 𝑑 的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。
如果我们的交叉验证集误差较大，我们如何判断是方差还是偏差呢？根据上面的图表，我们知道:
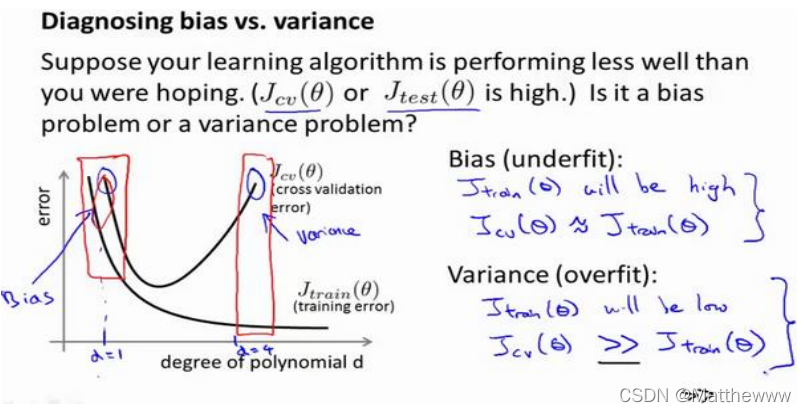
训练集误差和交叉验证集误差近似时：偏差/欠拟合
交叉验证集误差远大于训练集误差时：方差/过拟合
正则化和偏差/方差（Regularization and Bias_Variance）
在我们在训练模型的过程中，一般会使用一些正则化方法来防止过拟合。但是我们可能会正则化的程度太高或太小了，即我们在选择 λ 的值时也需要思考与刚才选择多项式模型次数类似的问题。
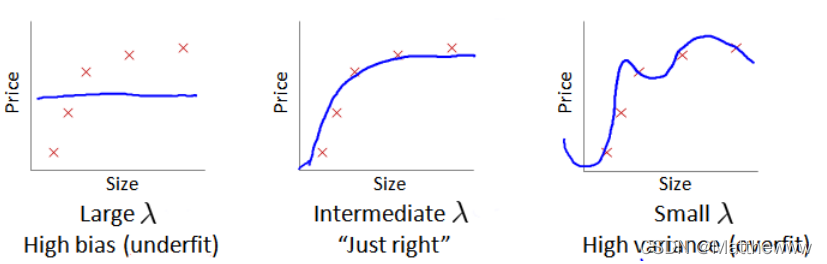
我们选择一系列的想要测试的 𝜆 值，通常是 0-10 之间的呈现 2 倍关系的值（如：0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10共 12 个）。我们同样把数据分为训练集、交叉验证集和测试集
选择𝜆的方法为：
1.使用训练集训练出 12 个不同程度正则化的模型
2.用 12 个模型分别对交叉验证集计算的出交叉验证误差
3.选择得出交叉验证误差最小的模型
4.运用步骤 3 中选出模型对测试集计算得出推广误差，我们也可以同时将训练集和交叉验证集模型的代价函数误差与 λ 的值绘制在一张图表上：
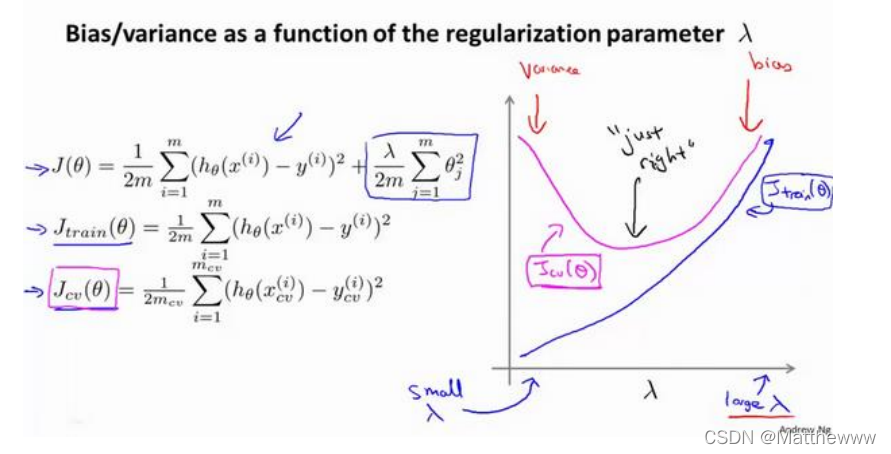
当 𝜆 较小时，训练集误差较小（过拟合）而交叉验证集误差较大
随着 𝜆 的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后增加
学习率（Learning Curves）
学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量（𝑚）的函数绘制的图表。即，如果我们有 100 行数据，我们从 1 行数据开始，逐渐学习更多行的数据。思想是：当训练较少行数据的时候，训练的模型将能够非常完美地适应较少的训练数据，但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据
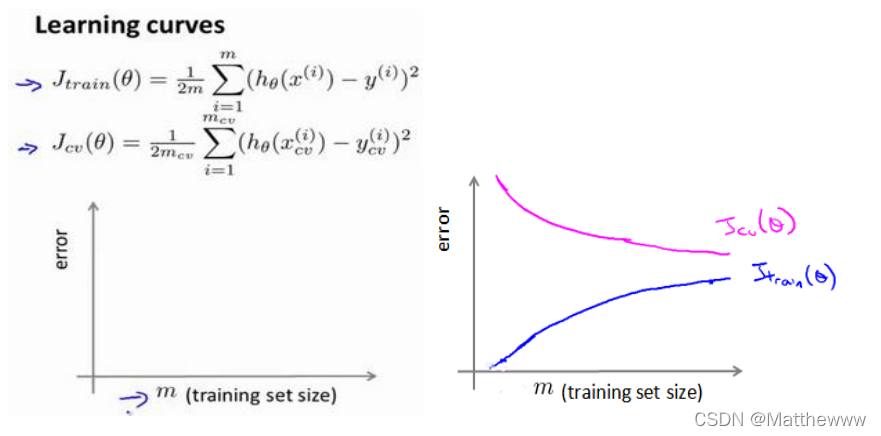
如何利用学习曲线识别高偏差/欠拟合：作为例子，我们尝试用一条直线来适应下面的数据，可以看出，在高偏差的情况下，随着训练集的增大，训练集误差会逐渐增大，最后接近交叉验证集误差（这是由于参数很少且有很多数据）：
也就是说在高偏差/欠拟合的情况下，我们会得到一个比较大的训练集误差和交叉验证集误差，并且增加数据到训练集不一定能有帮助。
如何利用学习曲线识别高方差/过拟合：假设我们使用一个非常高次的多项式模型，并且正则化非常小，可以看出，交叉验证集误差与训练集误差有一段很大的差距，当交叉验证集误差远大于训练集误差时，往训练集增加更多数据可以提高模型的效果。
也就是说在高方差/过拟合的情况下，增加更多数据到训练集可能可以提高算法效果。
总结
我们已经介绍了怎样评价一个学习算法，我们讨论了模型选择问题，偏差和方差的问题。那么这些诊断法则怎样帮助我们判断，哪些方法可能有助于改进学习算法的效果，而哪些可能是徒劳的呢？
让我们再次回到最开始的例子，在那里寻找答案，这就是我们之前的例子。回顾 最开始提出的六种可选的下一步，让我们来看一看我们在什么情况下应该怎样选择：
- 获得更多的训练实例——解决高方差
- 尝试减少特征的数量——解决高方差
- 尝试获得更多的特征——解决高偏差
- 尝试增加多项式特征——解决高偏差
- 尝试减少正则化程度 λ——解决高偏差
- 尝试增加正则化程度 λ——解决高方差
神经网络的方差和偏差：
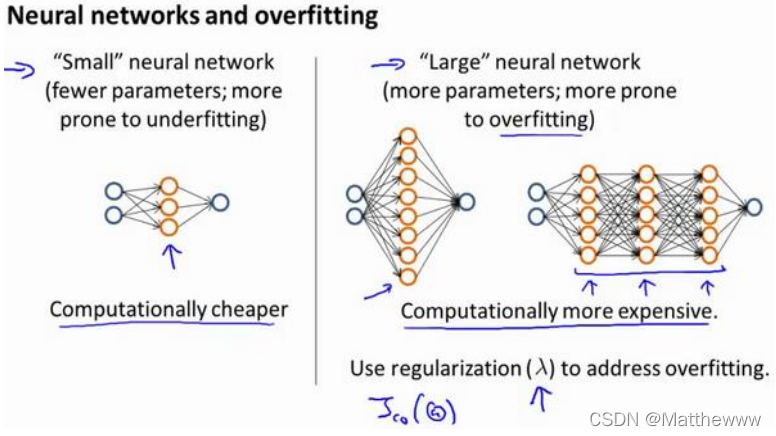
使用较小的神经网络，类似于参数较少的情况，容易导致高偏差和欠拟合，但计算代价较小使用较大的神经网络，类似于参数较多的情况，容易导致高方差和过拟合，虽然计算代价比较大，但是可以通过正则化手段来调整而更加适应数据。
通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好。
对于神经网络中的隐藏层的层数的选择，通常从一层开始逐渐增加层数，为了更好地作选择，可以把数据分为训练集、交叉验证集和测试集，针对不同隐藏层层数的神经网络训练神经网络， 然后选择交叉验证集代价最小的神经网络。