文章目录
神经网络基础与多类分类
3.1 模型表示
3.1.1 为什么需要神经网络
前两节所学习的无论是线性回归还是逻辑回归都存在一个缺点:当特征太多时,计算的负荷会非常大。例如在识别一张图片上是否是一辆汽车,我们将图片的像素视为特征,如果还需要特征组合形成多项式模型,那么可能会有上百万个特征,因此我们需要神经网络。
3.1.2 神经元与神经网络模型
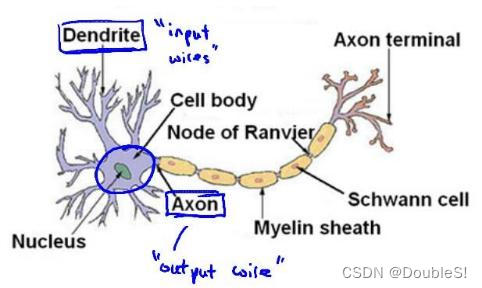
上图是一个神经元的示意图,每一个神经元可以被认为是一个处理单元/神经核,它含有许多输入/树突,并且有一个输出/轴突。
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元采纳特征作为输入,并根据神经元模型提供一个输出。下图是一个神经元示例,采用了逻辑回归模型作为自身学习模型。
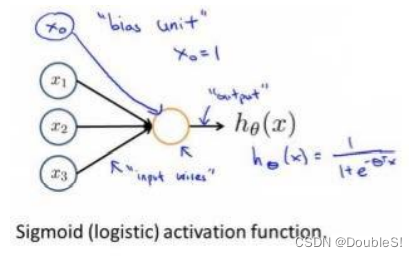
在神经网络中,参数
θ
\theta
θ 又被称为权重(weight).
神经网络模型是许多神经元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络。
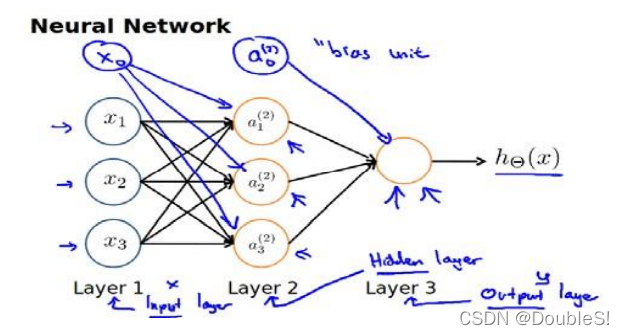
第一层为输入层,其中
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1?,x2?,x3?是输入单元,我们向它们输入原始数据。最后一层为输出层,其中的神经元称为输出单元,它负责计算
h
θ
(
x
)
h_\theta(x)
hθ?(x).中间层称为隐藏层,
a
1
,
a
2
,
a
3
a_1,a_2,a_3
a1?,a2?,a3?是中间单元,它们负责将数据进行处理,成为更“高级”的特征。与前两节引入
x
0
=
1
x_0=1
x0?=1一样,神经网络中也在非输出层都增加了一个偏差单位(bias unit).
我们引入标记法来帮助我们理解模型:
a
i
(
j
)
a_i^{(j)}
ai(j)?代表第
j
j
j层的第
i
i
i个激活单元。
Θ
(
j
)
\Theta^{(j)}
Θ(j)代表从第
j
j
j层映射到第
j
+
1
j+1
j+1层时的权重矩阵,其行数为下一层激活单元数,列数为当前层激活单元数加一(因为加了偏置单元),上图所示的
Θ
(
1
)
\Theta^{(1)}
Θ(1)的尺寸为
3
×
4
3\times4
3×4.上图中的激活单元与输出分别表达为:
a
1
(
2
)
=
g
(
θ
10
(
1
)
x
0
+
θ
11
(
1
)
x
1
+
θ
12
(
1
)
x
2
+
θ
13
(
1
)
x
3
)
a
2
(
2
)
=
g
(
θ
20
(
1
)
x
0
+
θ
21
(
1
)
x
1
+
θ
22
(
1
)
x
2
+
θ
23
(
1
)
x
3
)
a
3
(
2
)
=
g
(
θ
30
(
1
)
x
0
+
θ
31
(
1
)
x
1
+
θ
32
(
1
)
x
2
+
θ
33
(
1
)
x
3
)
h
θ
(
x
)
=
g
(
θ
10
(
2
)
a
0
+
θ
11
(
1
)
a
1
+
θ
12
(
2
)
a
2
+
θ
13
(
2
)
a
3
)
\begin{aligned} a_1^{(2)}=g(\theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1+\theta_{12}^{(1)}x_2+\theta_{13}^{(1)}x_3)\\ a_2^{(2)}=g(\theta_{20}^{(1)}x_0+\theta_{21}^{(1)}x_1+\theta_{22}^{(1)}x_2+\theta_{23}^{(1)}x_3)\\ a_3^{(2)}=g(\theta_{30}^{(1)}x_0+\theta_{31}^{(1)}x_1+\theta_{32}^{(1)}x_2+\theta_{33}^{(1)}x_3)\\ h_\theta(x)=g(\theta_{10}^{(2)}a_0+\theta_{11}^{(1)}a_1+\theta_{12}^{(2)}a_2+\theta_{13}^{(2)}a_3) \end{aligned}
a1(2)?=g(θ10(1)?x0?+θ11(1)?x1?+θ12(1)?x2?+θ13(1)?x3?)a2(2)?=g(θ20(1)?x0?+θ21(1)?x1?+θ22(1)?x2?+θ23(1)?x3?)a3(2)?=g(θ30(1)?x0?+θ31(1)?x1?+θ32(1)?x2?+θ33(1)?x3?)hθ?(x)=g(θ10(2)?a0?+θ11(1)?a1?+θ12(2)?a2?+θ13(2)?a3?)?
上面进行的讨论只是将特征矩阵其中一行(一个训练实例)喂给了神经网络,我们需要将整个数据集都喂给我们的神经网络来学习模型。由表达式我们可以得到每一个
a
a
a都是由上一层的所有
x
x
x和对应权重决定的,我们将这样从左到右的算法称为前向传播算法(FORWARD PROPAGATION)
前向传播算法相对于使用循环编码,利用向量化处理会更加简便,仍以上图为例,计算第二层激活单元的值。
X
=
[
x
0
x
1
x
2
x
3
]
z
(
2
)
=
[
z
1
(
2
)
z
2
(
2
)
z
3
(
3
)
]
{\begin{matrix} X=\begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} & z^{(2)} =\begin{bmatrix} z_1^{(2)}\\ z_2^{(2)}\\ z_3^{(3)} \end{bmatrix} \end{matrix}}
X=?????x0?x1?x2?x3????????z(2)=????z1(2)?z2(2)?z3(3)???????
z
(
2
)
=
Θ
(
1
)
x
a
(
2
)
=
g
(
z
(
2
)
)
z^{(2)}=\Theta^{(1)}x\\ a^{(2)}=g(z^{(2)})
z(2)=Θ(1)xa(2)=g(z(2))
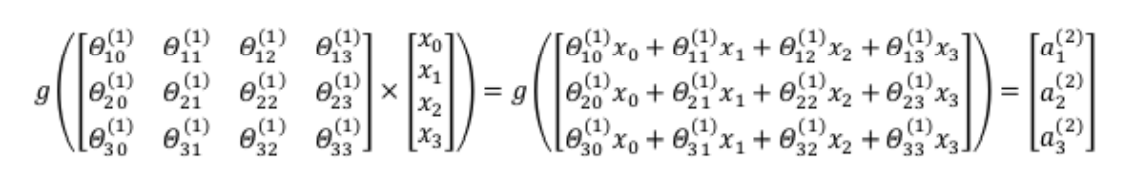
令
z
(
2
)
=
Θ
(
1
)
x
z^{(2)}=\Theta^{(1)}x
z(2)=Θ(1)x,则
a
(
2
)
=
g
(
z
(
2
)
)
a^{(2)}=g(z^{(2)})
a(2)=g(z(2)),计算后添加
a
0
(
2
)
=
1
a_0^{(2)}=1
a0(2)?=1.后计算输出的值为:
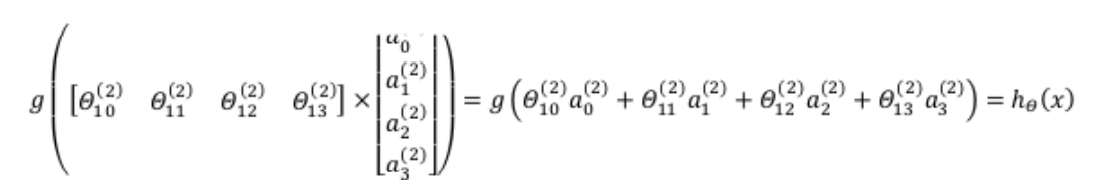
我们令
z
(
3
)
=
Θ
(
2
)
a
(
2
)
z^{(3)}=\Theta^{(2)}a^{(2)}
z(3)=Θ(2)a(2),则
h
θ
(
x
)
=
a
(
3
)
=
g
(
z
(
3
)
)
h_\theta(x)=a^{(3)}=g(z^{(3)})
hθ?(x)=a(3)=g(z(3)).
上面讨论的仅是一个训练实例所进行的计算。如果我们要对整个训练集进行计算,我们需要将训练集特征矩阵转置,使得同一个训练实例的特征在同一列里。即:
z
(
2
)
=
Θ
(
1
)
×
X
T
a
(
2
)
=
g
(
z
(
2
)
)
z^{(2)}=\Theta^{(1)}\times X^T\\ a^{(2)}=g(z^{(2)})
z(2)=Θ(1)×XTa(2)=g(z(2))
通过上面的表达式我们可以看出以sigmoid为模型的神经网络就像是Logistic regression,我们可以把中间层的激活单元看作更为高级的特征值,它们由
x
x
x决定,可以更好的预测新数据。
3.2 模型的直观理解
3.2.1 单层神经元
在神经网络中,输出层作出的预测利用的是隐藏层中的特征,而非输入层的原始特征,我们可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征。
我们通过一个单层神经元来表示逻辑运算,比如逻辑与、逻辑或。
举例说明:逻辑与(AND)

其中
θ
0
=
?
30
,
θ
1
=
20
,
θ
2
=
20
\theta_0=-30,\theta_1=20,\theta_2=20
θ0?=?30,θ1?=20,θ2?=20,输出函数即为
h
θ
(
x
)
=
g
(
?
30
+
20
x
1
+
20
x
2
)
.
h_\theta(x)=g(-30+20x_1+20x_2).
hθ?(x)=g(?30+20x1?+20x2?).
我们知道sigmoid函数的图像为:

z
=
4.6
z=4.6
z=4.6时,
g
(
z
)
≈
0.99
g(z)\approx0.99
g(z)≈0.99;
z
=
?
4.6
z=-4.6
z=?4.6时,
g
(
z
)
≈
0.01
g(z)\approx0.01
g(z)≈0.01

同理,OR函数可以如下表达:
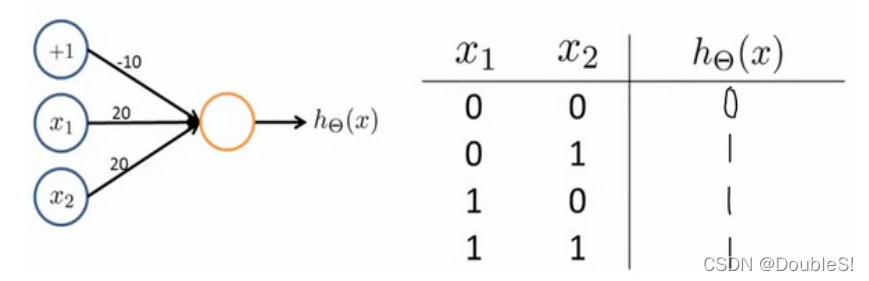
( N O T x 1 ) A N D ( N O T x 2 ) (NOTx_1)AND(NOTx_2) (NOTx1?)AND(NOTx2?)函数(或非函数)可以如下表达:
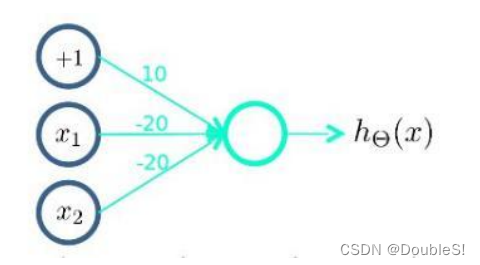
3.2.2 神经元组合
当我们想实现
X
N
O
R
XNOR
XNOR(同或)功能,
X
N
O
R
=
(
x
1
A
N
D
x
2
)
O
R
(
(
N
O
T
x
1
)
A
N
D
(
N
O
T
x
2
)
)
XNOR=(x_1 AND x_2)OR((NOT x_1)AND(NOTx_2))
XNOR=(x1?ANDx2?)OR((NOTx1?)AND(NOTx2?))
由此我们可以将单层神经元进行组合得到实现更复杂功能的函数表达。
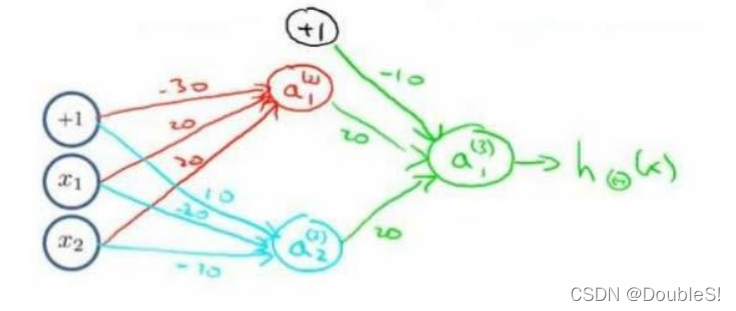
其中,
a
1
(
2
)
a_1^{(2)}
a1(2)?实现了
x
1
与
x
2
x_1与x_2
x1?与x2?的与运算,
a
2
(
2
)
a_2^{(2)}
a2(2)?实现了
x
1
与
x
2
x_1与x_2
x1?与x2?的或非运算,
a
1
(
3
)
a_1^{(3)}
a1(3)?实现了
a
1
(
2
)
与
a
2
(
2
)
a_1^{(2)}与a_2^{(2)}
a1(2)?与a2(2)?的或运算。
按这种方法我们可以逐渐构造出越来越复杂的函数,也能得到更强的特征。
3.3 多类分类
当我们不止有两个分类,比如通过图片识别路人、汽车、摩托车、卡车,输出层应该有4个值。
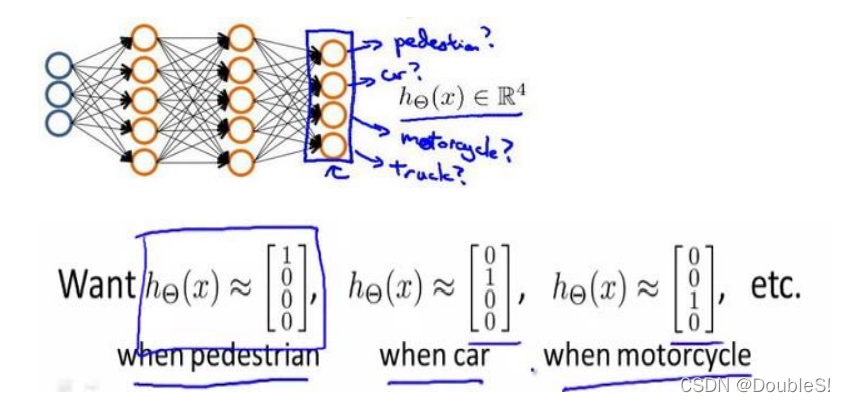
神经网络算法输出结果为四种可能情形之一:
[
1
0
0
0
]
[
0
1
0
0
]
[
0
0
1
0
]
[
0
0
0
1
]
\begin{matrix} \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} \begin{bmatrix} 0\\ 1\\ 0\\ 0 \end{bmatrix} \begin{bmatrix} 0\\ 0\\ 1\\ 0 \end{bmatrix} \begin{bmatrix} 0\\ 0\\ 0\\ 1 \end{bmatrix} \end{matrix}
?????1000???????????0100???????????0010???????????0001???????
3.4 配套作业的Python实现
3.4.1 Logistic regression实现多类分类
1.问题背景
您将使用逻辑回归和神经网络识别手写数字(从 0 到 9)。
自动手写数字识别在今天被广泛使用:从识别邮政编码(邮政编码)在邮件信封上识别银行支票上的金额。 此次练习将向您展示您所学的方法如何用于此分类任务。
2.代码实现
我们先导入我们所需要的库。
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as sio
import matplotlib
import scipy.optimize as opt
from sklearn.metrics import classification_report#这个包是评价报告
导入数据集,吴恩达给出的数据集是mat文件需要用scipy.io来加载数据。
与此同时,给出的数据集为(5000,400),400为20×20的灰度值,5000个训练实例。但是我们需要将20×20进行转置才能得到正确方向的图片。
def load_data(path, transpose=True):
data = sio.loadmat(path)
y = data.get('y') # (5000,1)
y = y.reshape(y.shape[0]) # make it back to column vector
X = data.get('X') # (5000,400)
if transpose:
# for this dataset, you need a transpose to get the orientation right
X = np.array([im.reshape((20, 20)).T for im in X])
# and I flat the image again to preserve the vector presentation
X = np.array([im.reshape(400) for im in X])
return X, y
X, y = load_data('ex3data1.mat')
print(X.shape)
print(y.shape)
我们可以通过数据集绘制图片,加深对灰度值和数据集的理解。
def plot_an_image(image):
"""
image : (400,)
"""
fig, ax = plt.subplots(figsize=(1, 1))
ax.matshow(image.reshape((20, 20)), cmap=matplotlib.cm.binary)
plt.xticks(np.array([])) # just get rid of ticks
plt.yticks(np.array([]))
pick_one = np.random.randint(0, 5000)
plot_an_image(X[pick_one, :])
plt.show()
print('this should be {}'.format(y[pick_one]))

需要注意的是,该数据集中0的y值为10.
def plot_100_image(X):
""" sample 100 image and show them
assume the image is square
X : (5000, 400)
"""
size = int(np.sqrt(X.shape[1]))
# sample 100 image, reshape, reorg it
sample_idx = np.random.choice(np.arange(X.shape[0]), 100) # 100*400
sample_images = X[sample_idx, :]
fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))
for r in range(10):
for c in range(10):
ax_array[r, c].matshow(sample_images[10 * r + c].reshape((size, size)),
cmap=matplotlib.cm.binary)
plt.xticks(np.array([]))
plt.yticks(np.array([]))
#绘图函数,画100张图片
plot_100_image(X)
plt.show()

raw_X, raw_y = load_data('ex3data1.mat')
print(raw_X.shape)
print(raw_y.shape)
(5000, 400)
(5000,)
首先,我们对数据进行整理。我们需要在X前插入一列1作为偏置单元。
# add intercept=1 for x0
X = np.insert(raw_X, 0, values=np.ones(raw_X.shape[0]), axis=1)#插入了第一列(全部为1)
X.shape
(5000, 401)
对y我们进行向量化标签处理,最后维数为10×5000,每一行都代表与该数字的关系,比如第一行,y[0]代表该样本是否为0.(因为我将10的行放在了第一行)依次类推,得到了各数字的二分类预测(是or不是),最终将得到输出向量。
# y have 10 categories here. 1..10, they represent digit 0 as category 10 because matlab index start at 1
# I'll ditit 0, index 0 again
y_matrix = []
for k in range(1, 11):
y_matrix.append((raw_y == k).astype(int)) # 见配图 "向量化标签.png"
# last one is k==10, it's digit 0, bring it to the first position,最后一行k=10,都是0,把最后一行放到第一行
y_matrix = [y_matrix[-1]] + y_matrix[:-1]
y = np.array(y_matrix)
print(y.shape)
# 扩展 5000 到 10*5000
# 比如 y=10 -> [0, 0, 0, 0, 0, 0, 0, 0, 0, 1]: ndarray为单独一列
我们从训练一维模型开始,也就是用逻辑回归实现二分类,比如判断该数字是否为0.我们可以直接利用上一节所写的代价函数与梯度函数。
"""
计算代价函数与梯度的矩阵计算方法
matrix *为矩阵乘法
array @为矩阵乘法 *为对应元素相乘
def cost(theta, X, y, l=1):
# INPUT:参数值theta,数据X,标签y,学习率
# OUTPUT:当前参数值下的交叉熵损失
# TODO:根据参数和输入的数据计算交叉熵损失函数
# STEP1:将theta, X, y转换为numpy类型的矩阵
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
# STEP2:根据公式计算损失函数(不含正则化)
cross_cost = np.mean(np.multiply(y, np.log(sigmoid(X * theta.T))) - np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T))))
# STEP3:根据公式计算损失函数中的正则化部分
reg = (l / (2 * len(X))) * np.power(theta[1:], 2).sum()
# STEP4:把上两步当中的结果加起来得到整体损失函数
whole_cost = cross_cost + reg
return whole_cost
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def gradient(theta, X, y, l=1):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y).T
parameters = int(theta.ravel().shape[1])
error = sigmoid(X * theta.T) - y
grad = ((X.T * error) / len(X)).T + ((l / len(X)) * theta)
# intercept gradient is not regularized
grad[0, 0] = np.sum(np.multiply(error, X[:, 0])) / len(X)
return np.array(grad).ravel()
"""
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def cost(theta, X, y, l=1):
''' cost fn is -l(theta) for you to minimize'''
return np.mean(-y * np.log(sigmoid(X @ theta)) - (1 - y) * np.log(1 - sigmoid(X @ theta)))
def regularized_cost(theta, X, y, l=1):
'''you don't penalize theta_0'''
theta_j1_to_n = theta[1:]
regularized_term = (l / (2 * len(X))) * np.power(theta_j1_to_n, 2).sum()
return cost(theta, X, y) + regularized_term
def regularized_gradient(theta, X, y, l=1):
'''still, leave theta_0 alone'''
theta_j1_to_n = theta[1:]
regularized_theta = (l / len(X)) * theta_j1_to_n
# by doing this, no offset is on theta_0
regularized_term = np.concatenate([np.array([0]), regularized_theta])
return gradient(theta, X, y) + regularized_term
def gradient(theta, X, y, l=1):
'''just 1 batch gradient'''
return (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y)
def logistic_regression(X, y, l=1):
"""generalized logistic regression
args:
X: feature matrix, (m, n+1) # with incercept x0=1
y: target vector, (m, )
l: lambda constant for regularization
return: trained parameters
"""
# init theta
theta = np.zeros(X.shape[1])
# train it
res = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient,
options={'disp': True}
)
# get trained parameters
final_theta = res.x
return final_theta
def predict(x, theta):
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int)
t0 = logistic_regression(X, y[0])
print(t0.shape)
y_pred = predict(X, t0)
print('Accuracy={}'.format(np.mean(y[0] == y_pred)))
(401,)
Accuracy=0.9974
下一步我们训练k维模型,生成输出向量,从而得到分类结果。
k_theta = np.array([logistic_regression(X, y[k]) for k in range(10)])
print(k_theta.shape)
(10, 401)
现在我们考虑k维模型在进行预测时的维度问题,需要用
X
×
θ
T
X\times \theta^T
X×θT.
(
5000
,
401
)
×
(
10
,
401
)
T
=
(
5000
,
10
)
(5000,401)×(10,401)^T=(5000,10)
(5000,401)×(10,401)T=(5000,10)
因此最终结果每一行为每个样本的输出向量,可以识别该数字。
prob_matrix = sigmoid(X @ k_theta.T)
# np.set_printoptions(suppress=True) 对很大/很小的数不采用科学计数法
y_pred = np.argmax(prob_matrix, axis=1) # 返回沿轴axis最大值的索引,axis=1代表行
y_answer = raw_y.copy() # 正确结果
y_answer[y_answer==10] = 0
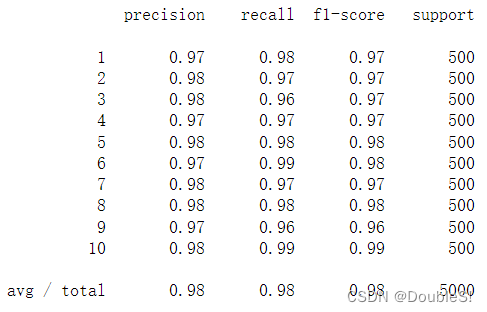
print(classification_report(y_answer, y_pred))
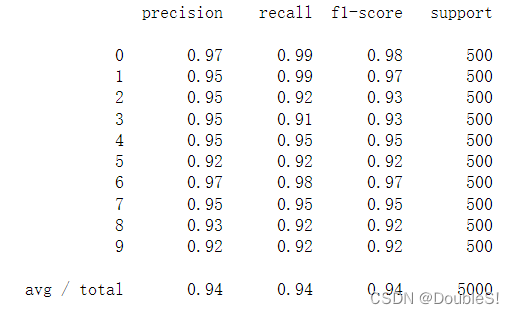
3.4.2 前向传播算法预测
1.问题背景
同3.4.1
2.模型展示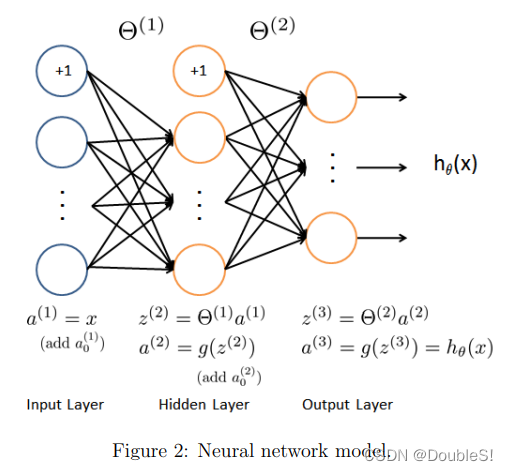
3.代码实现
def load_weight(path):
data = sio.loadmat(path)
return data['Theta1'], data['Theta2']
theta1, theta2 = load_weight('ex3weights.mat')
theta1.shape, theta2.shape
((25, 401), (10, 26))
可以得知,中间层神经元个数为25,算上偏置单元为26.
因为在数据加载函数中,原始数据做了转置,然而,转置的数据与给定的参数不兼容,因为这些参数是由原始数据训练的。 所以为了应用给定的参数,我需要使用原始数据(不转置)。
X, y = load_data('ex3data1.mat',transpose=False)
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # intercept
X.shape, y.shape
((5000, 401), (5000,))
数据准备好后,便可以开始进行feed forward prediction(前馈预测)
a1 = X
z2 = X @ theta1.T # (5000, 401) @ (25,401).T = (5000, 25)
a2 = sigmoid(z2)
a2 = np.insert(a2, 0, values=np.ones(a2.shape[0]), axis=1)
z3 = a2 @ theta2.T
a3 = sigmoid(z3)
y_pred = np.argmax(a3, axis=1) + 1 # numpy is 0 base index, +1 for matlab convention,返回沿轴axis最大值的索引,axis=1代表行
输出向量依次为是否为1,是否为2,……,是否为10(0),在python中下标从0开始,因此需要在结果中+1.
print(classification_report(y, y_pred))