[人工智能]图解神经网络：卷积、池化、全连接（通道数问题、kernel与filter的概念）

卷积操作

这个不难理解。我们知道图像在计算机中是由一个个的像素组成的，可以用矩阵表示。
假设一个5x5的输入图像，我们定义一个3x3的矩阵（其中的数值是随机生成的）

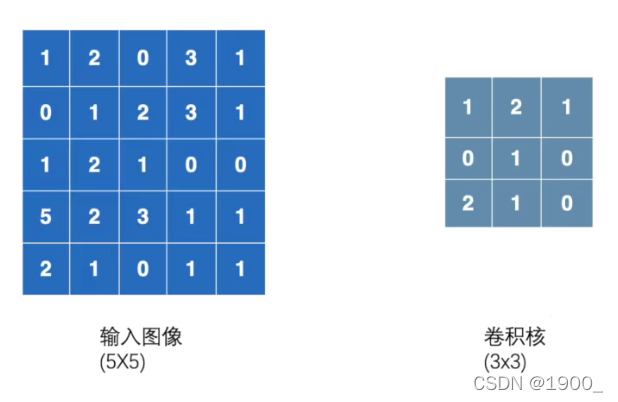
然后我们拿这个卷积核，在输入图像里面，选定左上角那个3x3的矩阵，用卷积核与这个矩阵对应的位置相乘，然后得到的9个数，这9个数再相加，最终得到一个结果。

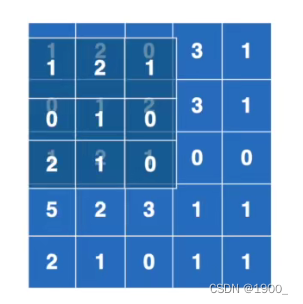
然后把卷积核往右边挪动一格，继续重复上述计算，再得到一个数字。

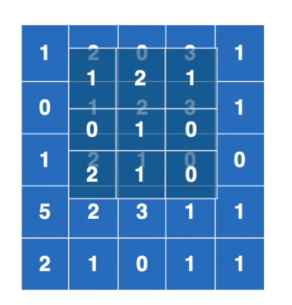
那么算完了，继续往右边挪，再算，

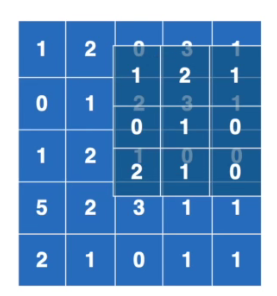
三次计算得到的值是

然后往下挪一格，继续重复上述操作，直到我们把整个5x5的输入图像全部计算完，得到了9个计算结果

这就是我们卷积的结果，这整个操作就是卷积操作。
那么有几个问题：

• Q1：每次往右挪动只能是1格吗？
• A1：不是，挪动1格，就是步长为1，如果我们设置步长为2，那就每次挪动2格，stride步长由我们设置
• Q2:卷积核里面的数值是怎么设置的？
• A2:随机生成的
• Q3：所以经过卷积之后，图像一定变小了？
• A3：不是的，上面的例子，5x5的输入，卷积之后得到3x3，那么我们如果给5x5的图像填充一圈，就变成了7x7的图像了，再去拿这个卷积核进行卷积，就会得到5x5的输出。实际中，我们也确实是这么做的，有一个参数padding即表示是否填充，我们可以设置填充的范围，以及填充的值，一般填充0。

顺便补充一个公式：
假设输入图片为 W x W 卷积核大小为FxF，步长stride=S，padding设置为P（填充的像素数）
则输出图像的大小=（W - F +2P）/S +1

那么，了解了整个卷积的过程，下面这个图就能看懂了。
这个图表示的是输入图像为5x5，卷积核为3x3，步长为1，padding=1，所以得到的输出是5x5

实际操作

卷积的流程是上面讲的那样，实际写代码的时候，我们可以不用那么麻烦，每一步都自己实现。
框架已经帮我们封装好的对应的函数，我们只需要调用函数，传给他相关参数即可。
我们以pytorch框架为例（tensorflow也差不多）
Conv2d操作时我们需要设置以下参数：

我们解释几个常用的：

• in_channels：输入的通道数
• out_channels：输出的通道数
• kernel_size：卷积核的大小，类型为int 或者元组，当卷积是方形的时候，只需要一个整数边长即可，卷积不是方形，要输入一个元组表示高和宽。（卷积核不需要你设置，只需要给定大小，里面的值是随机生成的）
• stride：步长（就是每次挪动几个像素，默认是1）
• padding：填充几圈，默认是0，不填充（填充的值为0）
• dilation：控制卷积核之间的间距（设置这个可以做空洞卷积）
• groups：控制输入和输出之间的连接
• bias：偏置，是否将一个 学习到的 bias 增加输出中，默认是True
• padding_mode：设置填充的模式

filter与kernel

这里重点解释以下通道数的问题：
假设一张图片是6x6的，通道数是1（如黑白图像），卷积核大小3x3，步长为1，不填充（padding为0）
我们暂时不考虑out_channels的设置问题，待会再说
也就是说现在的参数设置是：in_channels=1 kernel_size=3 stride=1 padding=0
这我们都能算出来，输出图像是4x4的，我画了个示意图，可以看下：

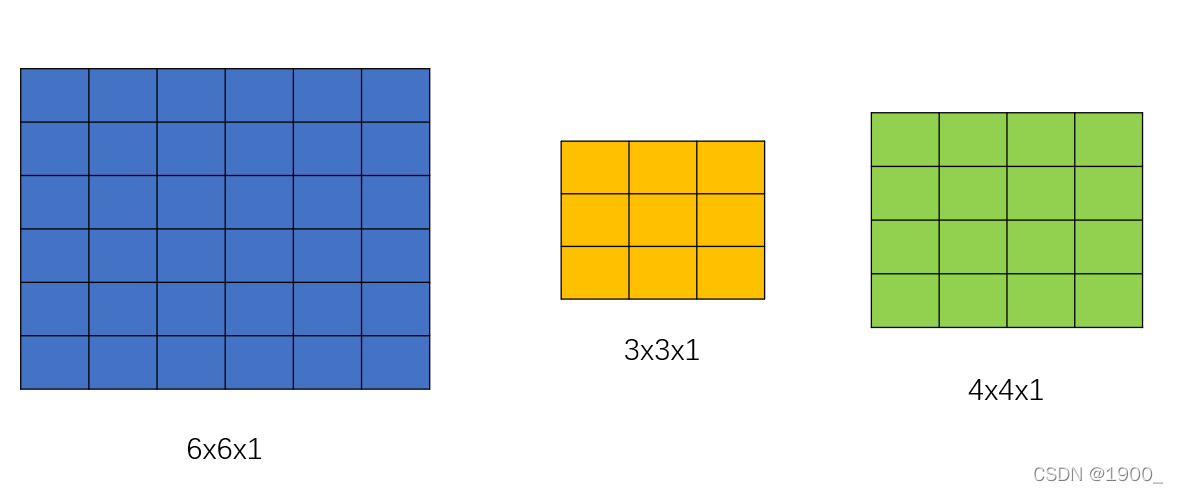
那我们也知道，rgb图像是三通道的，那么假如上图是个rgb图像呢，输出结果是多少呢
也就是说参数设置是：in_channels=3 kernel_size=3 stride=1 padding=0
如图：我们的输出结果依然是1通道的。

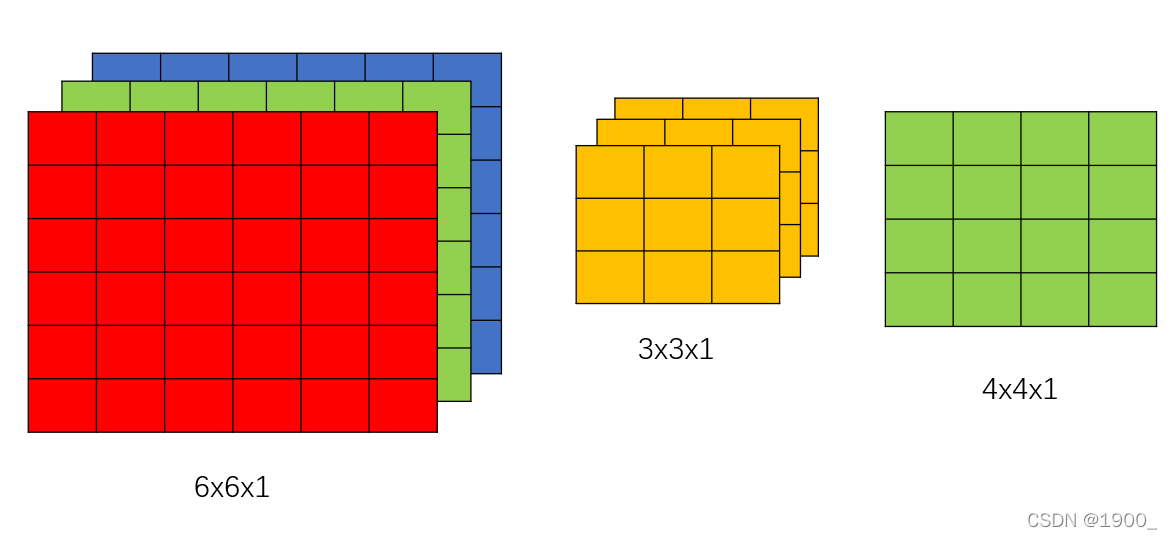
可以看到，这里的卷积核变了，变成了三个叠加。
有些同学就是只明白上面那个单通道的卷积操作，但是不明白这个多通道的卷积操作。
当你输入图像是三通道的时候，卷积核就也是三通道的。
其实关键点就在于in_channels，in_channels是输入的通道数，同时它也是滤波器（filter）的通道数。
kernel我们叫做卷积核，大小是3x3，如果三个卷积核叠在一起，我们叫filter滤波器。

当你输入图像是三通道的时候，卷积核就也是三通道的。
他们之间的运算是由这三个kernel组成的这个filter（有27个数），去和输入图像的对应位置做运算。
27个数分别与输入图像中的27个数字对应相乘，然后再相加，得到一个数，重复这个计算，把整个输入图像都走一遍，就得到9个数。
如图：

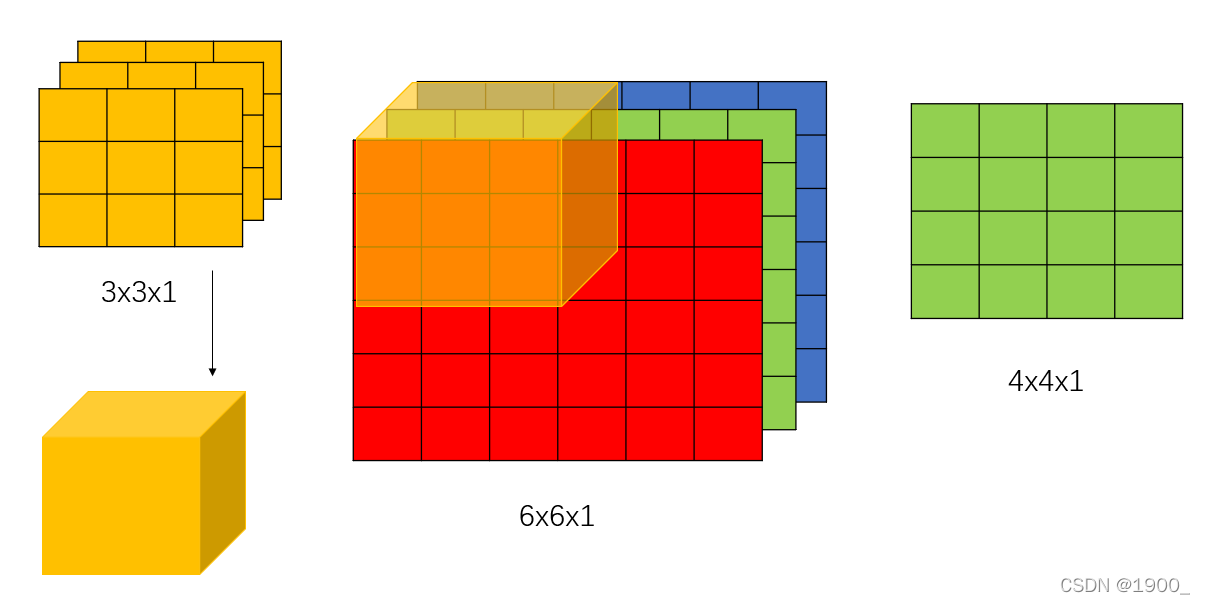
所以运算出来的也是一维的结果，也就是单通道的结果。

所以，kernel和filter的概念就明白了。
kernel: 内核是一个2维矩阵，长 × 宽。
filter：滤波器是一个三维立方体，长× 宽 × 深度， 其中深度便是由 多少张内核构成。
可以说kernel 是filter 的基本元素， 多张kernel 组成一个filter。

（ps：我看到有的博客或者文章里面也把三层叠起来的这个立方体叫做卷积核，可能是从英文过渡到中文上，有的人觉得表达意思即可，所以就随口说的，我觉得这个叫法是不准确的，不过吧明白意思即可。尽量用kernel和filter，避免混淆）。

那么有两个问题：
一个filter 中应该包含多少张 kernel 呢？
答案是：由输入的通道数in_channels来确定
一层中应该有多少个filter呢？
答案是：看我们想要提取多少个特征，一个filter 负责提取某一种特征，我们想输出多少个特征就设置多少个filter。
那么设置filter的参数是什么呢？
就是前面我们没说的out_channels
不要忘了，out_channels也是可以人为设置的，上面那个图，一个filter运算得到的结果是单通道的，假如你设置out_channels=2
那么就会得到输出通道为2。如图所示：

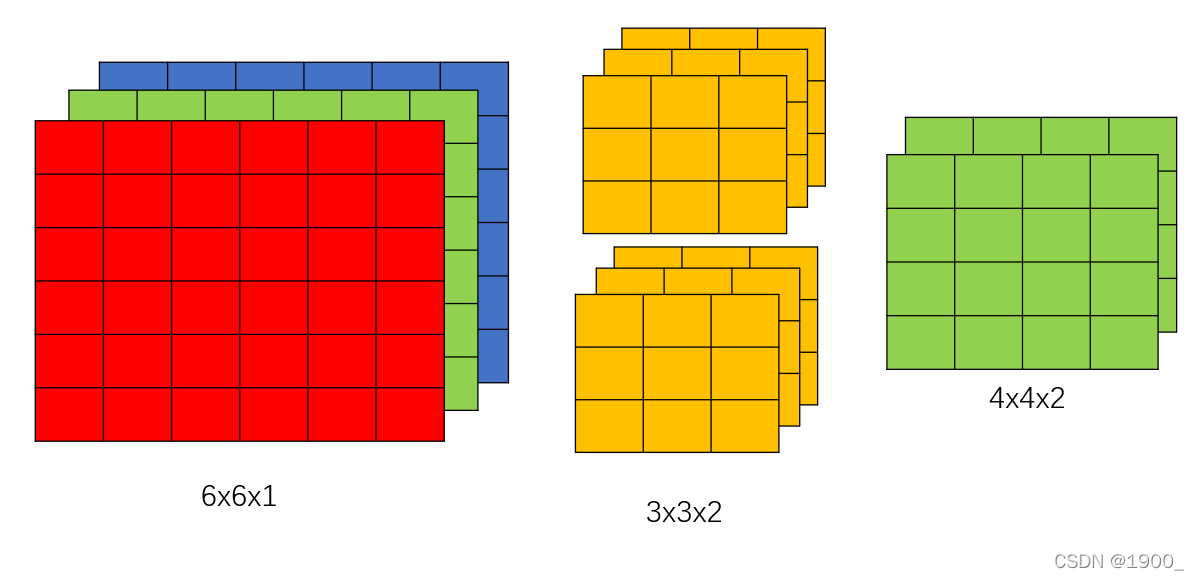
所以。总结一下就是。

in_channels决定了filter的通道数，out_channels的设置决定了filter的数量，这一层卷积得到的结果的out_channels就是下一层的in_channels。
所以，out_channels和in_channels是没有关系的。

可视化的例子

我们可以用一个实际的网络LeNET5来看一下我们刚才的解释。
LeNET5第一层是一个卷积层，其输入数据是32x32x1，卷积核大小5x5，步长=1，padding=0，输出为6 @ 28×28
那么，这里输入是单通道的，也就是in_channels=1，那么filter的深度也就是1了，但是输出通道要求是6，也就是out_channels=6
也就是需要6个filter，最终得到6个28x28的图像。
如图：这是整个LeNET5的网络可视化模型，蓝色的那个是32x32的，经过卷积，得到了下一层，也就是黄色的那一层，你可以看到，黄色的那一层是一个立方体，我们可以把他展开看看

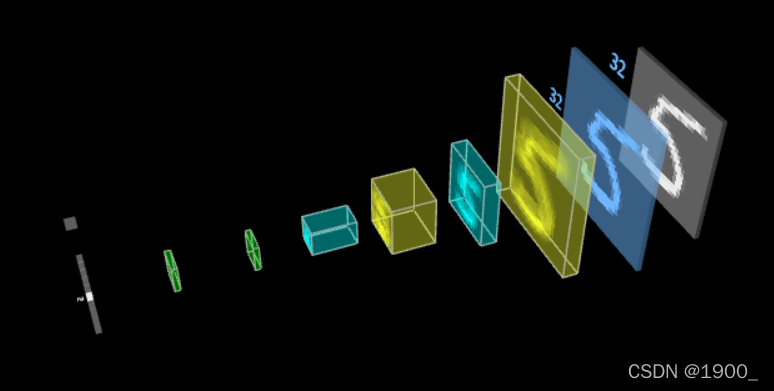
可以看到：展开后确实就是6个28x28的结果

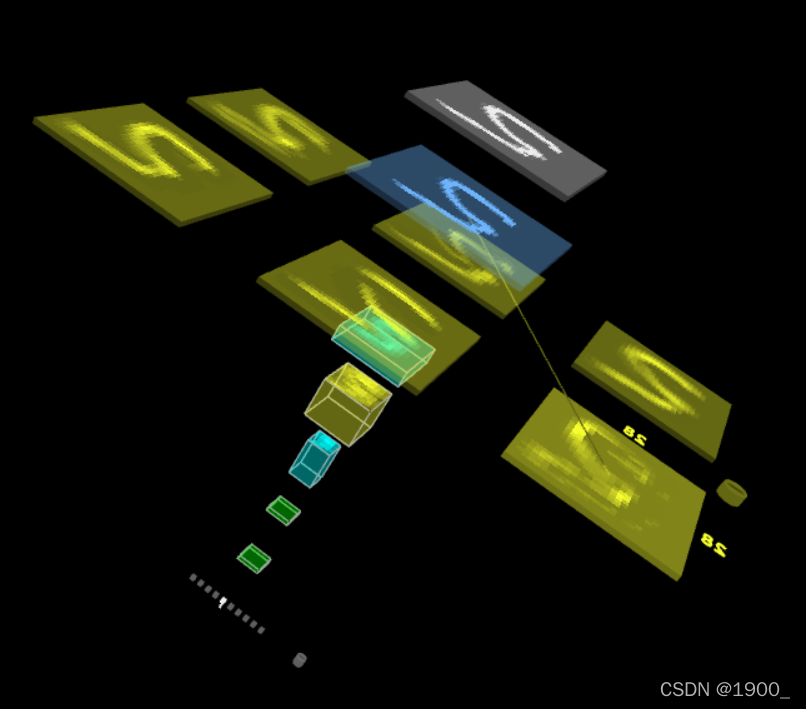
这个可视化的网站地址是：https://tensorspace.org/index.html

池化

明白了卷积操作，池化就简单多了。池化操作就是用一个kernel，比如3x3的，就去输入图像上对应3x3的位置上，选取这九个数字中最大的作为输出结果。这就叫最大池化。

全连接

全连接层一般在卷积神经网络的末尾。他的输入呢是前面卷积池化得到的结果，把结果“展平”，就是把得到的结果矩阵，平铺为一个列向量。那么全连接如何对这个列向量运算呢？

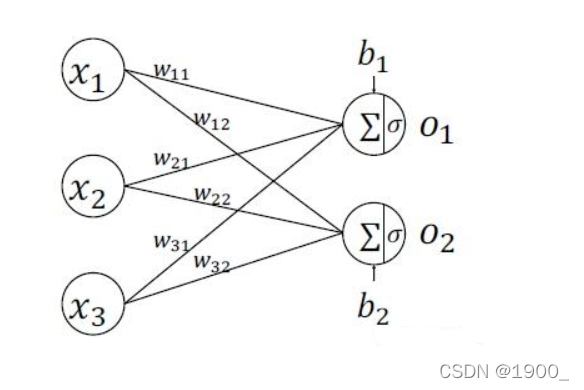
如图，假设左边的x1,x2,x3就是我们展平后得到的向量，那么我们用$x_1\times w_{11}+x_2\times w_{21}+x_3\times w_{31}=b_1$
同理，b2也是这么算出来的。这个计算过程可以表示为矩阵运算

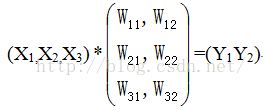
那么这个运算中，只要我们增加w矩阵的列数，就可以得到不同的结果数量。比如w设置为3x3的，那就会得到1x3的记过。所以呢，全连接层输出一列向量，最终得到的结果数量是我们可以定义的。
那么这么做有什么意义呢？
全连接层（fully connected layers，FC）在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。
这么做可以减少特征位置对分类带来的影响，本来feature map是一个矩阵，所以特征的位置对分类是有影响的，比如识别图像里面的猫，猫在图像的左上角，那么左上角就可以检测到，右下角就检测不到，但是呢，我们那这个二维的矩阵，通过全连接层，整合成一个值输出，这个值就是对猫的预测概率，不论猫在哪，只要概率大，就是有猫。这样做忽略了空间结构特征，增强了鲁棒性。