这节我们介绍监督学习中分类方法的支持向量机(SVM),我尽量少用数学公式,多用形象的语言去讲清楚基本概念。
定义
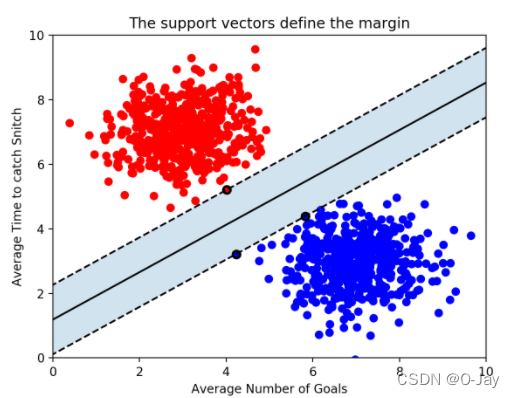
SVM是用于分类的监督学习模型,使用支持向量来定义决策边界,支持向量是每一类最接近决策边界的点,如上图中用黑色圈圈起来的点,你可能会问,这不是点吗?为什么说成是向量?把原点和圈住的点相连,它就成向量啦哈哈。所以一堆数据给我们,我们关注的只有其中的几个能做支持向量的点(如果数据特征有n个,则只有要用n+1个支持向量)(其他点可以忽视哈哈),效率非常高。通过将未标记的点与决策边界进行比较就可以进行分类! 支持向量与决策边界之间的距离称为间隔(margin),支持向量机试图在可接受的误差范围内创造尽可能大的间隔。
?
数学表达
我们定义决策平面(也叫超平面)为
w
T
x
+
b
=
0
\textbf w^T\textbf x+b=0
wTx+b=0,w,x是向量,w法向量决定了超平面的方向,b位移项决定了超平面与原点的距离,空间中任意的点到超平面的距离为r,由初中学的距离公式可知
r
=
∣
w
T
x
+
b
∣
∣
∣
w
∣
∣
r = \frac{|\textbf w^T\textbf x + b|}{||\textbf w||}
r=∣∣w∣∣∣wTx+b∣? 假设超平面能正确分类数据,我们定义 (y是标签):
{
w
T
x
i
+
b
?
+
1
,
y
i
=
+
1
w
T
x
i
+
b
?
?
1
,
y
i
=
?
1
\begin{cases} &w^Tx_i + b\geqslant +1,\quad y_i=+1 \\ &w^Tx_i + b\leqslant -1,\quad y_i=-1 \end{cases}
{?wTxi?+b?+1,yi?=+1wTxi?+b??1,yi?=?1? 所以
y
i
?
(
w
T
x
i
+
b
)
?
1
y_i\cdot (w^Tx_i + b) \geqslant 1
yi??(wTxi?+b)?1, 对于支持向量,
{
w
T
x
i
+
b
=
+
1
,
y
i
=
+
1
w
T
x
i
+
b
=
?
1
,
y
i
=
?
1
\begin{cases} &w^Tx_i + b= +1,\quad y_i=+1 \\ &w^Tx_i + b= -1,\quad y_i=-1 \end{cases}
{?wTxi?+b=+1,yi?=+1wTxi?+b=?1,yi?=?1? 所以
y
i
?
(
w
T
x
i
+
b
)
=
1
y_i\cdot (w^Tx_i + b) = 1
yi??(wTxi?+b)=1,我们终于可以推出margin的表达式了:
r
=
∣
w
T
x
+
b
∣
∣
∣
w
∣
∣
=
∣
y
i
?
(
w
T
x
+
b
)
∣
∣
∣
w
∣
∣
=
y
i
?
(
w
T
x
+
b
)
∣
∣
w
∣
∣
\begin{aligned} r &= \frac{|w^T x + b|}{||w||} = \frac{|y_i\cdot(w^T x + b)|}{||w||} \\ &= \frac{y_i\cdot(w^T x + b)}{||w||} \end{aligned}
r?=∣∣w∣∣∣wTx+b∣?=∣∣w∣∣∣yi??(wTx+b)∣?=∣∣w∣∣yi??(wTx+b)?? 所以
m
a
r
g
i
n
=
m
i
n
r
margin = min{\textbf r}
margin=minr , 而
m
i
n
{
y
i
?
(
w
T
x
+
b
)
}
=
1
min\{y_i\cdot(w^T x + b)\} = 1
min{yi??(wTx+b)}=1,所以:
margin
=
1
||w||
\textbf{margin} = \frac{\textbf 1}{\textbf {||w||}}
margin=||w||1? 终于,我们得出了SVM的基本型(max margin 即 min w)(s.t.是subject to 的意思,就是受哪些条件限制):
min
?
w
,
b
1
2
∣
∣
w
∣
∣
2
s
.
t
.
y
i
?
(
w
T
x
i
+
b
)
?
1
,
i
=
1
,
2
,
…
,
m
.
\begin{aligned} &\min_{w,b} \frac{1}{2}||w||^2\\ &s.t. \quad y_i\cdot (w^Tx_i + b)\geqslant 1,\quad i=1,2,\dots,m. \end{aligned}
?w,bmin?21?∣∣w∣∣2s.t.yi??(wTxi?+b)?1,i=1,2,…,m.?
问题来了,怎么去求w,b?
我们进入对偶问题,不要害怕,我不引入数学公式了。我们看看上面的基本型,一个多元函数,然后受一些条件限制,然后目标是求它的极值,高数学得好的同学应该有灵感了,没错,这就是多元函数的条件极值问题,最简单的就是用拉格朗日函数法嘛,先引入拉格朗日乘子
α
i
\alpha_i
αi?,然后构建拉格朗日函数
L
(
w
,
b
,
α
)
L(w,b,\alpha)
L(w,b,α),再分别对w,b 求导并令为0,再把两式带回拉格朗日函数消去w和b得
L
(
α
)
L(\alpha)
L(α),求其最大值时的
α
\alpha
α,紧接着再求出w,b,搞定。
这只是大概思路,深入的话你会发现这是个二次规划问题,需要引入KKT条件和推导很多数学式子,还会了解到高效的SMO算法,慢慢来比较快。
?
软间隔
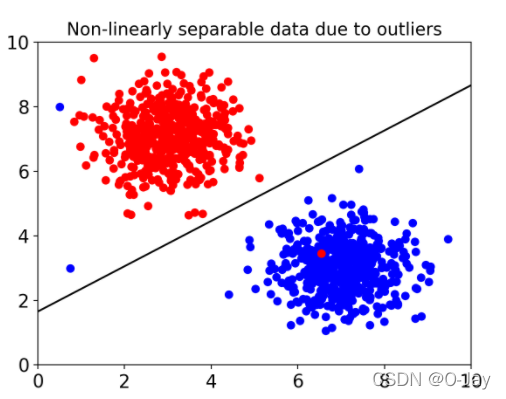
遇到上面这种情况怎么办?不可能精准地将两部分严格分开,那我们就不那么严格地分开,哈哈,称为软间隔分类(soft-margin),就是允许有一定的误差,以大局为重,总的来说能分开就算合格。
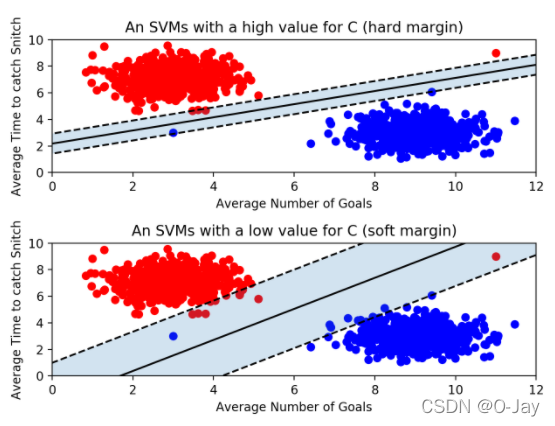
我们引入一个参数C,它决定支持向量机允许多少误差。如果C很大,那么支持向量机有一个硬边缘,它不会允许很多错误分类,因此,边缘可以相当小。如果C太大,太宽容,模型就有过拟合的风险。
ξ
\xi
ξ是松弛变量。
min
?
w
,
b
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
m
ξ
i
s
.
t
.
y
i
?
(
w
T
x
i
+
b
)
?
1
?
ξ
i
,
ξ
i
?
0
,
i
=
1
,
2
,
…
,
m
.
\begin{aligned} &\min_{w,b} \frac{1}{2}||w||^2 + C \sum_{i=1}^{m} \xi^i\\ &s.t. \quad y_i\cdot (w^Tx_i + b)\geqslant 1- \xi^i,\quad \xi^i \geqslant 0,\quad i=1,2,\dots,m. \end{aligned}
?w,bmin?21?∣∣w∣∣2+Ci=1∑m?ξis.t.yi??(wTxi?+b)?1?ξi,ξi?0,i=1,2,…,m.?
?
核函数
核函数里面会有很多数学推导,这里以先熟悉概念为主。
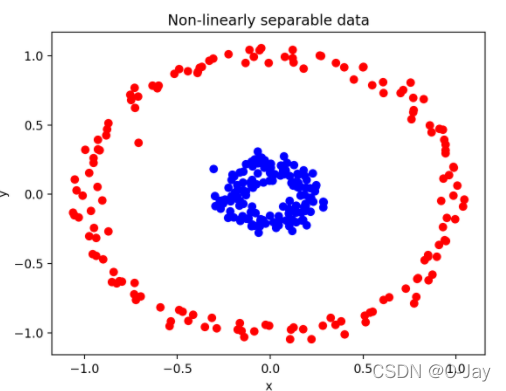
遇到这种数据怎么办?再软也不行了,这就不是直线能够分开的。我们引入核函数,就是把数据先映射到高维空间,在高维空间用超平面把它们分开,然后再把超平面投影回原始维度即为所求。核函数就是把低维数据投影到高纬的函数
比如这个核函数,点(1,2)经过投影得(
2
2
2\sqrt{2}
22?,1,4)
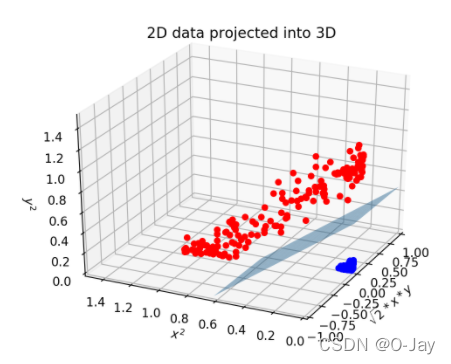
在高维空间得到可靠的超平面后,投影回二维平面,得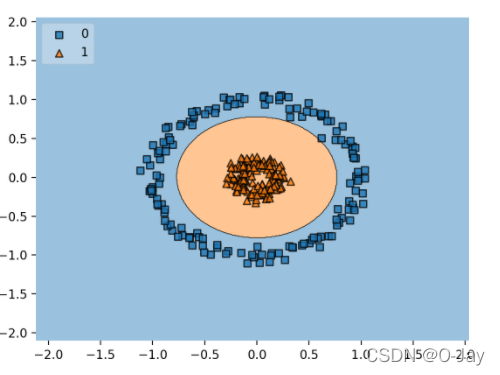
这个橙色圆的外边即为所求。