[人工智能]深度强化学习Actor-Critic的更新逻辑梳理笔记

深度强化学习Actor-Critic的更新逻辑梳理笔记

前言：

前几天在给师弟讲actor-critic架构更新逻辑的时候，actor的优化逻辑我卡了好一会儿，最终也没有完整的把逻辑梳理出来，今天刚好趁着脑子清醒，把之前的PPT拿出来，借着PPT的内容，将AC架构的更新逻辑说明白，特此做一个笔记。

Actor-Critic架构简介：

关于AC架构，还是简单的说说我的理解吧，对于强化来说，目的是找到一个最优策略模型，使得它的动作轨迹累计回报值最大。自然会有一个策略模型，这里称作为Actor，它的输入是当前的状态信息state，输出为动作action。如果没有评价网络critic的话，那就只能利用轨迹的累计回报来更新参数了，一条轨迹更新一次，效率较低。所以有人想出来，要不要整个评价模型，对于特定的状态和动作，直接给出一个评价值，用来指导actor的优化方向。

critic的更新逻辑

而评价模型critic评价值的依据是什么呢？如果有之前的强化基础知识的话，对(s, a)的评价，就是Q(s, a)=r+γ*Q(s’,a’)，这就是贝尔曼方程的Q值形式，关于贝尔曼方程的理解，我好像也做过笔记。

有了上面的等式，假设Q(s’, a’)是已知的，s, a, r, s’ 都是已知的，那么只需要更新critic的参数φ，使得Q(s,a|φ)的输出接近r+γ*Q(s’,a’)即可。这是一个有监督学习，属于深度学习的基本操作。

至于Q(s’,a’)到底准不准，在DDPG算法中，Q(s’,a’|φ-target)的更新频率要低于Q(s,a|φ)，类似于人走路的时候，左脚先固定不动，右脚往前迈，然后左脚再往前走，一步一步往前挪~

这里我们已经拿到了critic的更新方式了，只要我们拥有足够多的(s, a, r, s’)，那么我们就能获取到一个很好的评价模型，对于特定的(s,a)都能给一个“中肯”的评价。

actor的更新逻辑：

那这个评价怎么更新actor模型呢？
我们看看它的表达式：
actor的式子：$a=\pi (s|\theta )$
critic的式子：$q=Q(s,a|?)=Q(s,\pi (s|\theta )|?)$

而更新actor的思路是，对于特定状态s，调整actor模型参数θ，使得actor的输出$\pi (s|\theta )$，经过critic模型后的输出$Q(s,\pi (s|\theta )|?)$往更大的方向更新。

很明显这需要对一个复合函数进行链式求导。
整体来看，函数$Q(s,\pi (s|\theta )|?)$，当critic参数φ不变和特定的状态s情况下，Q是一个关于actor参数θ的复合函数，链式求导可得：

$J=\delta Q/\delta \theta =(\delta Q(s,a)/\delta \pi (s|\theta ))?(\delta \pi (s|\theta )/\delta \theta )$

拿到了导数，根据定义，θ沿着梯度向上更新，即可使得$Q(s,\pi (s))$的值变大，即actor的输出会变得更好。

贴上DDPG算法流程图：

其中核心公式就是下面这个：

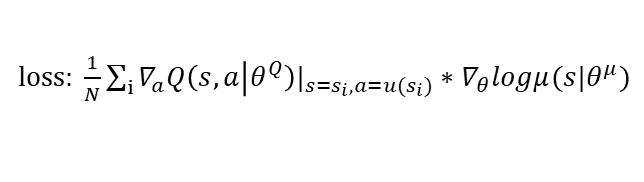
这里的a=u(s)，u(s)即$\pi (s)$，由于确定性策略，所以写成了u(s)，而那个log只是一个技巧，方便计算。