注意力机制是指我们将视觉注意力集中在图像的不同区域,或者将注意力集中在一句话中的某个词语,以下图为例:

人类的视觉注意力允许我们以“高分辨率”关注某个特定区域(例如黄色框内的耳朵)同时以“低分辨率”处理周围的环境信息(例如下雪的背景),接下来我们转移关注点或者直接根据关注点作出相应的判断。给定一张图片的一些patch,其余部分的像素提供给我们patch所在区域是什么的信息。我们期望在黄框内看到一个耳朵,这是因为我们已经看到了一只狗鼻子、另外一个耳朵以及狗狗的眼睛(红框内的物体)。然而,毛衣和毯子对于判断狗狗特征是毫无帮助的。
类似地,我们可以解释某个句子中的单词之间的关系。当我们看见“吃”这个词时,我们希望马上遇到一个食物的单词。下面的带颜色的单词描述了事物,但是这没有和“吃”直接相连:
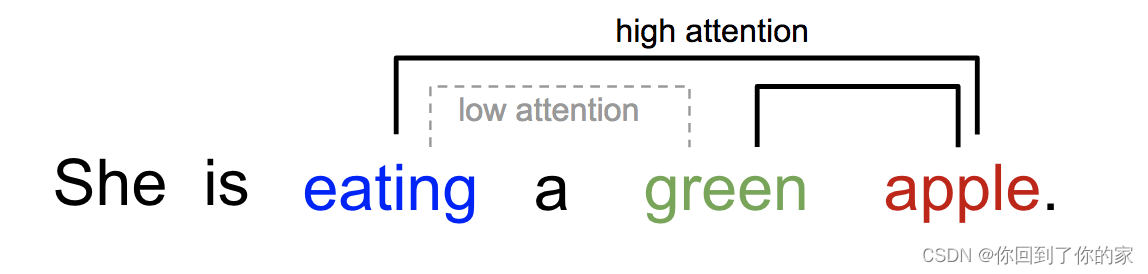
简言之,深度学习中的注意力机制可以被广义地解释为重要性权重向量:为了预测或者推断某个元素,例如图片中的一个像素,或者句子中的一个单词,我们使用注意力向量估计它与其他元素(在论文中这个过程被称为“attend to”)的相关性有多强,并将它们的值与注意力向量加权之后的值之和作为目标的近似值。
Seq2Seq模型存在的问题
seq2seq模型起源于语言处理模型(Sutskever, et al. 2014),广义来讲,它的目的是将输入序列转换为一个新的输出序列,两者之间可以长度相等也可以不等。转化任务的例子包括各种语言之间的翻译(文本中的或者音频中的),问答生成或者将句子翻译为语法树。
seq2seq模型通常来讲有一个编码-解码结构,由如下部分组成:
- 编码器处理输入序列并将信息压缩为固定长度的context向量(这也被称为sentence embedding或者“thought”向量)。这种表达方式期望获取整个输入序列的一个较好的总结信息。
- 解码器由context初始化,然后生成转化后的输出。早期工作仅使用解码网络的最后状态作为解码器的初始状态。
编码器和解码器都是循环神经网络,例如使用LSTM或者GRU元素,下图是seq2seq模型的示例:
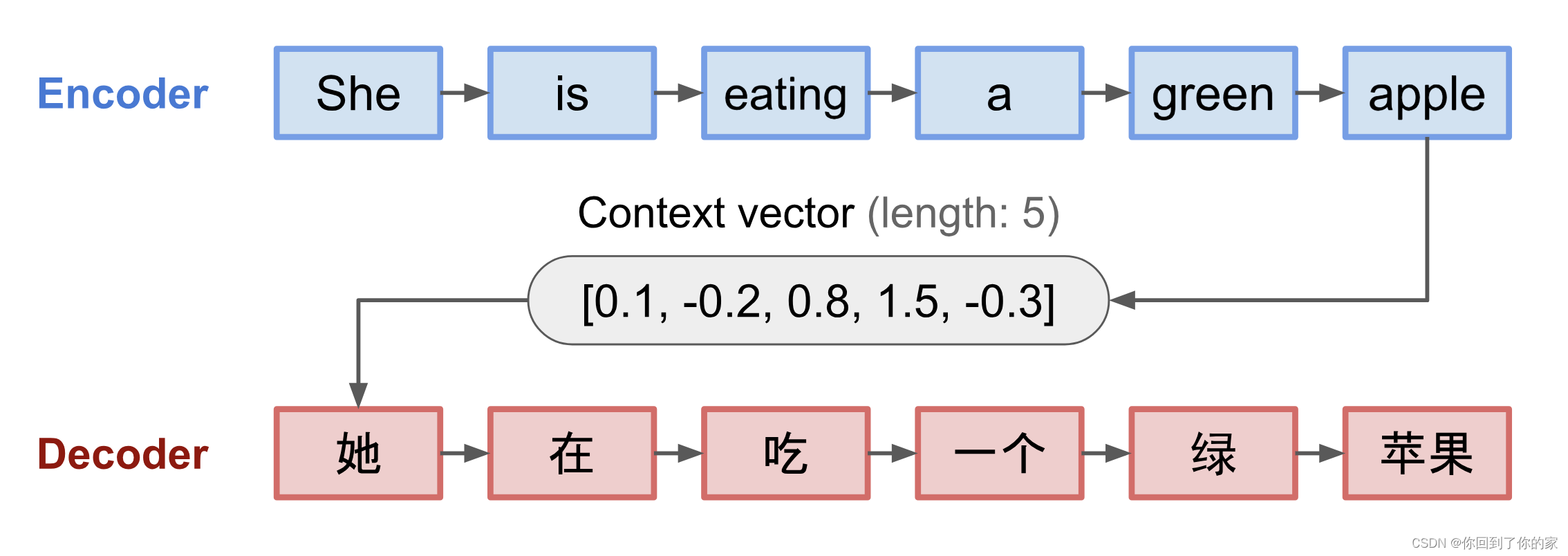
固定长度的context vector的一个致命缺陷是缺乏记忆长句子的能力。通常它在处理完整个输入后会遗忘前面的信息。attention机制在2015年被提出来解决这个问题(Bahdanau et al., 2015)
attention机制的提出
attention机制提出是为了帮助记忆机器翻译(neural machine translation,NMT)中的长句子。attention机制提出了一种独特的方式,创建了context向量以及整个输入间的shortcuts。The weights of these shortcut connections are customizable for each output element.
由于context向量可以访问整个输入序列,我们不需要担心遗忘的问题。The alignment between the source and target is learned and controlled by the context vector. Essentially the context vector consumes three pieces of information:
- 编码器隐藏状态
- 解码器隐藏状态
- alignment between source and target
定义
接下来我们定义NMT中提出的attention机制。举例来说,我们有一个长度为n的输入序列 x \mathbf{x} x并且想要输出一个长度为m的目标序列 y \mathbf{y} y:
x = [ x 1 , x 2 , … , x n ] y = [ y 1 , y 2 , … , y m ] \mathbf{x}=[x_1,x_2,\dots,x_n]\quad\mathbf{y}=[y_1,y_2,\dots,y_m] x=[x1?,x2?,…,xn?]y=[y1?,y2?,…,ym?]
注意黑体表示是向量,这在本文的其他部分也适用。
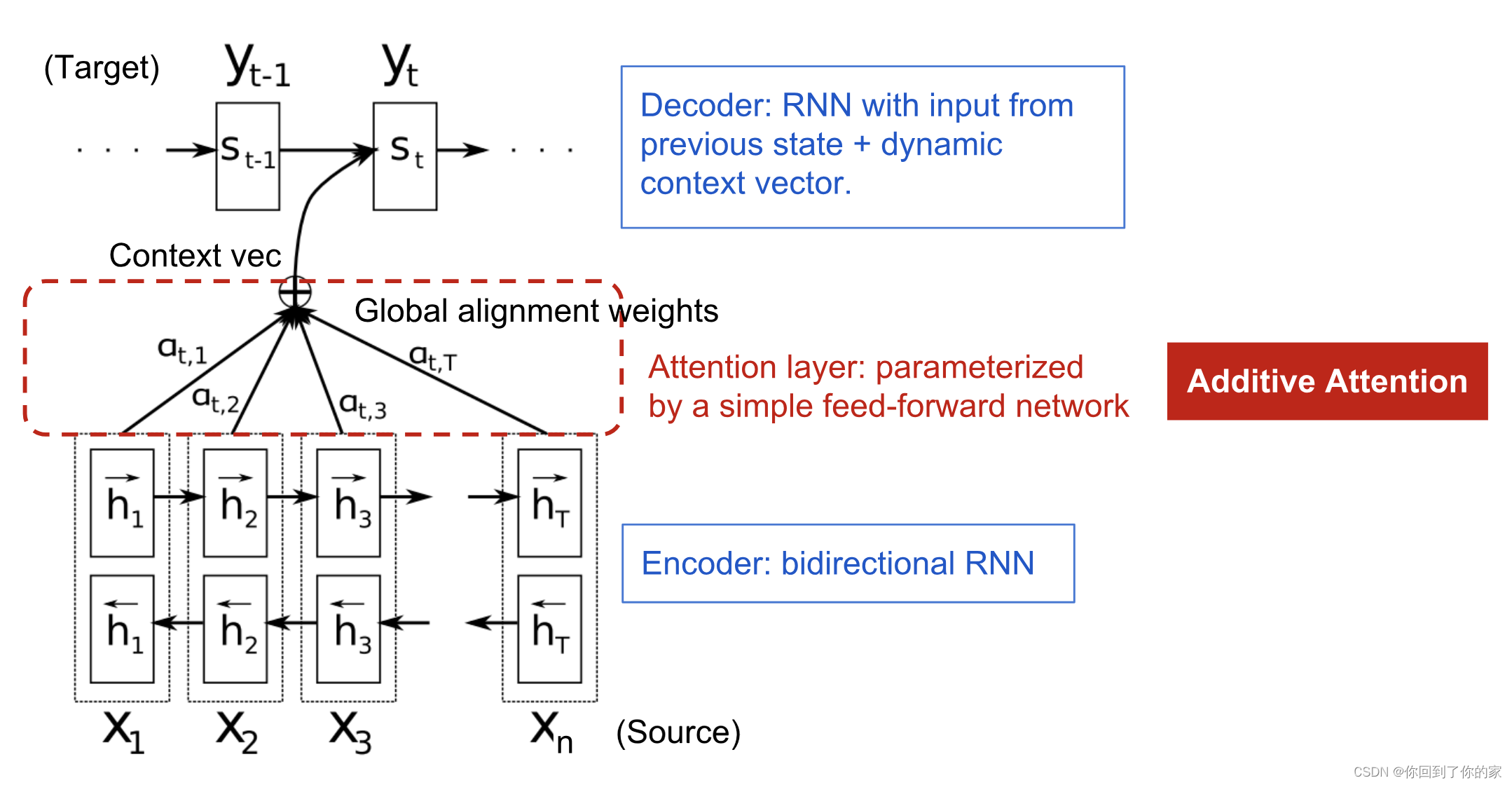
编码器是一个带有forward隐藏状态 h → i \overrightarrow{\boldsymbol{h}}_i hi? 以及反向隐藏状态 h ← i \overleftarrow{\boldsymbol{h}}_i hi? 的双向RNN(循环网络)。这两个的简单拼接表示编码器状态。其出发点是在处理某个单词时包括它前面以及后面单词的信息:
h i = [ h → i ? ; h ← i ? ] ? , i = 1 , … , n \boldsymbol{h}_i = [\overrightarrow{\boldsymbol{h}}_i^\top; \overleftarrow{\boldsymbol{h}}_i^\top]^\top, i=1,\dots,n hi?=[hi??;hi??]?,i=1,…,n
解码器网络包含位置为 t ( t = 1 , … , m ) t (t=1,\dots,m) t(t=1,…,m) 处的输出单词的隐藏状态 s t = f ( s t ? 1 , y t ? 1 , c t ) \boldsymbol{s}_t=f(\boldsymbol{s}_{t-1}, y_{t-1}, \mathbf{c}_t) st?=f(st?1?,yt?1?,ct?) ,这里context向量 c t \mathbf{c}_t ct?是输入序列隐藏状态的和,weighted by alignment scores:
c t = ∑ i = 1 n α t , i h i ;?Context?vector?for?output? y t α t , i = align ( y t , x i ) ;?How?well?two?words? y t ?and? x i ?are?aligned. = exp ? ( score ( s t ? 1 , h i ) ) ∑ i ′ = 1 n exp ? ( score ( s t ? 1 , h i ′ ) ) ;?Softmax?of?some?predefined?alignment?score. . \begin{aligned} \mathbf{c}_t &= \sum_{i=1}^n \alpha_{t,i} \boldsymbol{h}_i & \small{\text{; Context vector for output }y_t}\\ \alpha_{t,i} &= \text{align}(y_t, x_i) & \small{\text{; How well two words }y_t\text{ and }x_i\text{ are aligned.}}\\ &= \frac{\exp(\text{score}(\boldsymbol{s}_{t-1}, \boldsymbol{h}_i))}{\sum_{i'=1}^n \exp(\text{score}(\boldsymbol{s}_{t-1}, \boldsymbol{h}_{i'}))} & \small{\text{; Softmax of some predefined alignment score.}}. \end{aligned} ct?αt,i??=i=1∑n?αt,i?hi?=align(yt?,xi?)=∑i′=1n?exp(score(st?1?,hi′?))exp(score(st?1?,hi?))??;?Context?vector?for?output?yt?;?How?well?two?words?yt??and?xi??are?aligned.;?Softmax?of?some?predefined?alignment?score..?
alignment模型将一个分数 α t , i \alpha_{t,i} αt,i? 分配给输入位置为i以及输出位置为t的一个组合,值取决于它们之间的匹配度。 { α t , i } \{\alpha_{t, i}\} {αt,i?} 集合 are weights defining how much of each source hidden state should be considered for each output. 在Bahdanau的论文中,alignment score α \alpha α 由一个单隐藏层的前馈神经网络进行参数化,并且这个网络和模型中的其他部分一起进行训练。score function因此选用如下格式(将tanh用作非线性激活函数):
score ( s t , h i ) = v a ? tanh ? ( W a [ s t ; h i ] ) \text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \mathbf{v}_a^\top \tanh(\mathbf{W}_a[\boldsymbol{s}_t; \boldsymbol{h}_i]) score(st?,hi?)=va??tanh(Wa?[st?;hi?])
这里 v a \mathbf{v}_a va?以及 W a \mathbf{W}_a Wa?都是alignment模型中要学习的权重矩阵。
alignment score矩阵能够明确显示源词和目标词之间的相关性。

Attention机制家族
总结
下表总结了几个流行的注意力机制以及它们对应的alignment score函数:
| 名字 | alignment score 函数 | 引用 |
|---|---|---|
| Content-base attention | score ( s t , h i ) = cosine [ s t , h i ] \text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \text{cosine}[\boldsymbol{s}_t, \boldsymbol{h}_i] score(st?,hi?)=cosine[st?,hi?] | Graves2014 |
| Additive(*) | score ( s t , h i ) = v a ? tanh ? ( W a [ s t ; h i ] ) \text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \mathbf{v}_a^\top \tanh(\mathbf{W}_a[\boldsymbol{s}_t; \boldsymbol{h}_i]) score(st?,hi?)=va??tanh(Wa?[st?;hi?]) | Bahdanau2015 |
| Location-Base | α t , i = softmax ( W a s t ) \alpha_{t,i} = \text{softmax}(\mathbf{W}_a \boldsymbol{s}_t) αt,i?=softmax(Wa?st?)(注意,这简化了softmax alignment,仅仅依赖于目标位置) | Luong2015 |
| General | score ( s t , h i ) = s t ? W a h i \text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \boldsymbol{s}_t^\top\mathbf{W}_a\boldsymbol{h}_i score(st?,hi?)=st??Wa?hi?(这里 W a \mathbf{W}_a Wa?是attention层的一个可训练权重参数矩阵 | Luong2015 |
| Dot-Product | score ( s t , h i ) = s t ? h i \text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \boldsymbol{s}_t^\top\boldsymbol{h}_i score(st?,hi?)=st??hi? | Luong2015 |
| Scaled Dot-Product(^) | score ( s t , h i ) = s t ? h i n \text{score}(\boldsymbol{s}_t, \boldsymbol{h}_i) = \frac{\boldsymbol{s}_t^\top\boldsymbol{h}_i}{\sqrt{n}} score(st?,hi?)=n?st??hi??(注意这和dot-product attention仅相差了一个缩放因子,这里n是source隐藏状态的维度 | Vaswani2017 |
(*) Referred to as “concat” in Luong, et al., 2015 and as “additive attention” in Vaswani, et al., 2017.
(^) It adds a scaling factor (1/\sqrt{n}), motivated by the concern when the input is large, the softmax function may have an extremely small gradient, hard for efficient learning.
如下是广义类别的attention机制的一个总结:
| 名字 | 定义 | 引用 |
|---|---|---|
| Self-Attention(&) | Relating different positions of the same input sequence. Theoretically the self-attention can adopt any score functions above, but just replace the target sequence with the same input sequence. | Cheng2016 |
| Global/Soft | Attending to the entire input state space. | Xu2015 |
| Local/Hard | Attending to the part of input state space; i.e. a patch of the input image. | Xu2015; Luong2015 |
(&) Also, referred to as “intra-attention” in Cheng et al., 2016 and some other papers.
Self-Attention
Self-attenion,同样被称为intra-attention,是一种将单个序列中不同位置关联起来以计算这个序列的某种表达方式的attention机制。这种attention已经被证明在machine reading、abstractive summarization以及image description generation领域十分有效。
long short-term memory网络论文中使用self-attention来进行machine reading。在下面的例子中,self-attention机制使得我们可以学习到当前单词以及句子中之前部分单词之间的相关性。

上图中当前单词用红色标注,蓝色阴影的大小表示activation level。
Soft以及Hard Attention
在 show, attend and tell 论文中,注意力机制用于生成captions. 图片首先被CNN处理来提取特征。接下来一个LSTM解码器使用卷积特征来每次逐个生成descriptive words,权重通过attention机制学习。The visualization of the attention weights clearly demonstrates which regions of the image the model is paying attention to so as to output a certain word.

上图中最终输出的句子是“A woman is throwing a frisbee in a park.”,图片来自于Xu et al. 2015中的图6b。
This paper first proposed the distinction between “soft” vs “hard” attention, based on whether the attention has access to the entire image or only a patch:
- Soft Attention:alignment权重are learned and placed “softly” over all patches in the source image; essentially the same type of attention as in Bahdanau et al., 2015.
优点:模型是平滑可微分的
缺点:当输入很大时计算量大 - Hard Attention:only selects one patch of the image to attend to at a time.
优点:less calculation at the inference time.
缺点:模型无法微分并且需要more complicated techniques such as variance reduction or reinforcement learning to train. (Luong, et al., 2015)
Global以及Local Attention对比
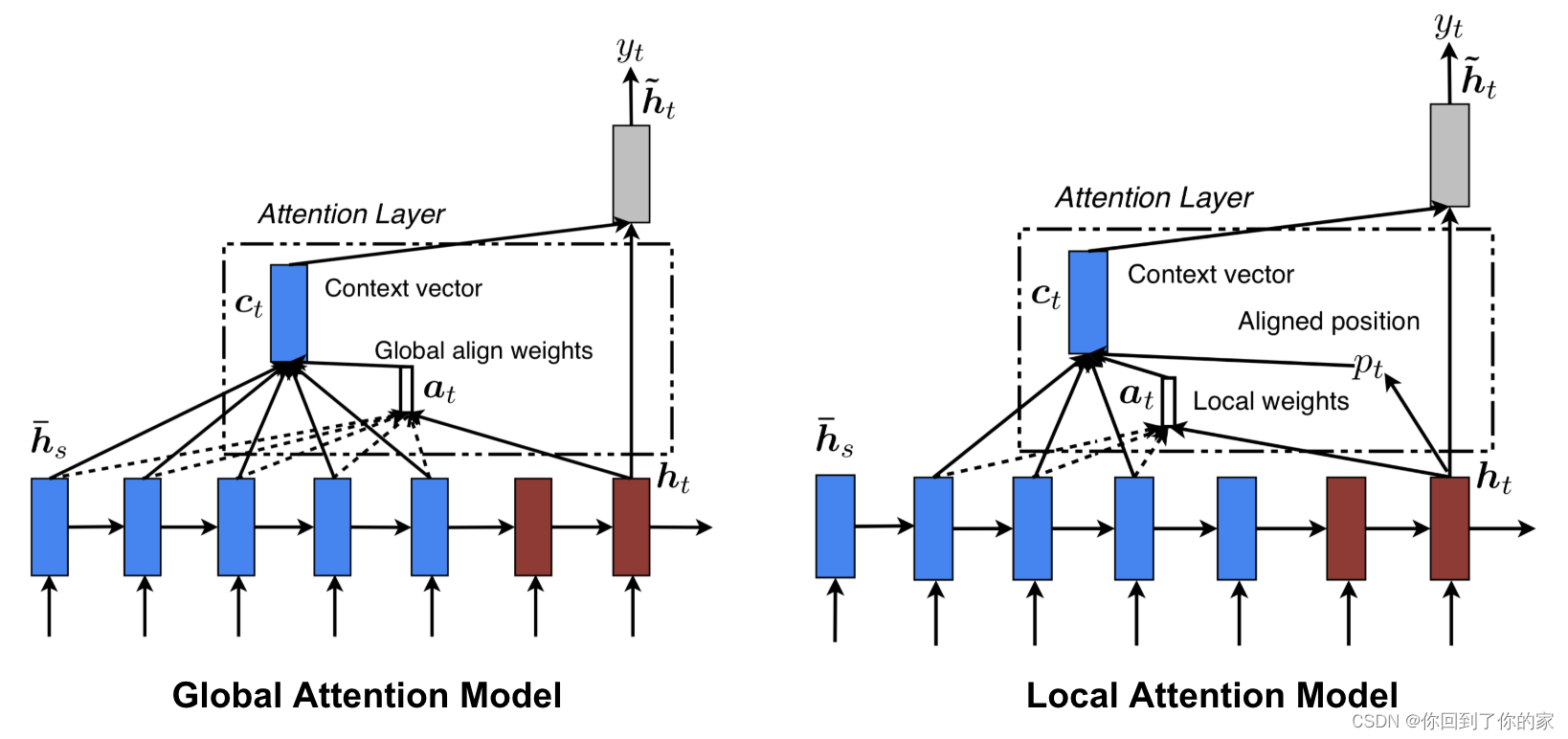
Luong, et al., 2015 proposed the “global” and “local” attention. The global attention is similar to the soft attention, while the local one is an interesting blend between hard and soft, an improvement over the hard attention to make it differentiable: the model first predicts a single aligned position for the current target word and a window centered around the source position is then used to compute a context vector.
Neural Turing Machines
Pointer网络
Transformer
“Attention is All you Need” (Vaswani, et al., 2017), without a doubt, is one of the most impactful and interesting paper in 2017. It presented a lot of improvements to the soft attention and make it possible to do seq2seq modeling without recurrent network units. The proposed “transformer” model is entirely built on the self-attention mechanisms without using sequence-aligned recurrent architecture.
The secret recipe is carried in its model architecture.
Key,Value以及Query
transformer中最主要的组成部分就是multi-head self-attention机制。transformer将输入的编码表示为一组键值对 ( K , V ) (\mathbf{K}, \mathbf{V}) (K,V), 两者的维度均为 n n n(输入的序列长度),在NMT文中,keys以及values都是编码器的隐藏状态。在decoder中,先前的输出被压缩为一个维度为m的query Q \mathbf{Q} Q,下一个输出通过将这个query以及对应的keys以及values进行mapping得到。
transformer采用scaled dot-product attention:输出是values的加权和,这里分配给每个value的权重通过query和所有keys的dot-product确定:
Attention ( Q , K , V ) = softmax ( Q K ? n ) V \text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{n}})\mathbf{V} Attention(Q,K,V)=softmax(n?QK??)V